基于FAHP和K-Means聚类的边坡稳定性模型

2019-01-21，，

长江科学院院报 2019年1期

，，

(1.辽宁工程技术大学土木工程学院，辽宁阜新 123000； 2.中交隧道局第二工程有限公司，西安 710000)

1 研究背景

边坡稳定性是一个综合系统，各个因素对边坡稳定性的影响是非线性的和不确定性的。实际工程中边坡岩土体遇水后发生的土体的水解、溶解、不均匀膨胀、黏聚力降低等一系列复杂的变化，对边坡稳定性产生影响。而这些影响因素在计算安全系数时是不被考虑的，并且在计算安全系数时不同的计算方法得出的结果也会出现较大的偏差。这说明了传统的安全系数法在确定边坡状态时具有一定的局限性。

边坡系统中包含着能够定量描述的因素和难以定量描述的因素，两者共同决定边坡的状态。由内摩擦角、高度、边坡角等定量的土体力学参数计算得出的安全系数[1-2]只能对边坡稳定性作出一个综合评价，是确定边坡状态的因素之一。而边坡在水作用下产生的渗流作用、冲刷作用等对稳定性的影响是难以在实际中被定量描述的，但往往能观测到孔隙水压力比的变化，故用孔隙水压力比来表示边坡中水对边坡稳定性的影响程度。再基于定性和定量分析相结合的思想，运用模糊层次分析法[3-6](Fuzzy Analytic Hierarchy Process,FAHP) 和K-Means[7]聚类算法，通过对中交隧道局二公司近2 a修建的项目进行数据采集分析，提出基于FAHP和K-Means聚类算法的边坡稳定性模型，运用本模型对新建南昌到赣州铁路客运专线高铁项目的2个边坡进行了验证研究，且取得了较好的成果，避免了实际工程中单纯运用安全系数确定边坡状态的局限性，具有较高的实用性。

2 FAHP法确定权重

各种因素对边坡稳定的影响程度在传统的理论中是不便于确定的[8]，对此引入多人评价的FAHP法对权重进行评价。FAHP法比传统的层次分析法[9-10](Analytic Hierarchy Process,AHP)更加贴合实际，运用三角模糊函数确定多人模糊化评价矩阵，通过计算、去模糊化、标准化等步骤得到各影响因素的权重。

2.1 多人评价模糊化矩阵

构建三角模糊化函数为

式中：m为使隶属度为1的评价权重值；x为各因素的评价权重值；l′为所属区间下界；u′为所属区间上界；在本文的三角模糊函数中x0=m；μm(x)为三角模糊函数。

三角形模糊函数的成员函数图像如图1所示。

图1 三角形模糊函数的成员函数Fig.1 A member function of a triangular fuzzy function

根据评价权重运用三角模糊函数的成员函数建立多人评价模糊评价矩阵为

(2)

其中，

式中：l,x,u分别代表重要程度的下限值、最有可能值和上限值；n为边坡样本的个数；A为各个影响因素的重要性评价矩阵。

2.2 计算模糊化后各个元素的权重

对模糊矩阵进行整合使得每个样本最终只有一个因素向量。均值向量和初始权向量分别为：

(3)

2.3 去模糊化计算公式

通过对初始权重向量的计算和修正得到最终的最终评价权重向量，即

v(D1≥D2)=

式中：v(D1≥D2)为D1比D2重要的可能度；x1为D1的初始中值；x2为D2的初始中值；u1为D1的初始值的上界；l2为D2的初始值的下界。

di=minV(Di≥Dj) ,j≠i，j=1,…,n。

(6)

式中di为最终评价权重。

2.4 进行标准化

将得到的各因素最终评价权重除所有最终评价权重的和，对其进行标准化计算，即

(7)

式中wi为各个因素的权重。

式中w为权重向量，由此得到各个因素对边坡稳定性的权重。

3 自分类的聚类方法

实际中常规方法很难对边坡进行准确的分类，对此提出自分类的聚类方法。在一个具有n个样本的样本矩阵内首先通过自分类运算把所有样本分成c类(c≤n/3)。在完成对样本的划分后运用相对于聚类中心的广义加权距离，联系数向量等构建边坡稳定性模型。

3.1 基于相似度的分类

首先建立一个有n个样本，每个样本有m个评价因素的样本矩阵X。取样本矩阵中X的一个样本向量xa作为初始聚类中心，用剩下的样本与xa进行比较，可以得到剩余样本的隶属度矩阵(式(8))。

(8)

式中：rij为各因素隶属度值；xij为各因素归一化后的值；xia为随机选取某一样本的各因素归一化值。

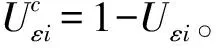
(9)

(10)

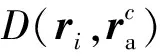
根据距离最小化原则建立关于隶属度向量Uε和归一化样本向量ri的函数为：

F(Uεi,rij)=D(ri,rac)+D(ri,ra) ;

(11)

(12)

式中F(Uεi,rij)为相对聚类中心距离的和。

求F(Uεi,rij)在0≤Uεi≤1,0≤rij≤1条件下的最小值，首先对函数求偏导为

(13)

当Uεi=0,ri=(0,0,…,0)时，代入函数可得到minF(Uεi,rij)=-1，因为F(Uεi,rij)函数代表2个曼哈顿权距离[11]的和，所以F(Uεi,rij)≥0。令minF(Uεi,rij)=0，把结果代入式(11)，可以得到相似度Uεi的公式，即

(14)

通过式(14)可以得到样本xi对xa的相似度Uεi，当Uεi≥δ时样本xi和xa属于一类。δ为最终确定样本分类的标准值。在所有n个样本中，属于第一类的有b个样本。第一次分类后再运用以上的分类方法对剩下n-b个样本继续进行运算，重复此过程直到把所有样本划分成c个类，并且得到相应的相似度向量Uε。

3.2 已知分类的聚类推导

已知样本矩阵X分类的情况下求各个类的聚类中心、相对距离矩阵、联系数向量等完成对模型的构建。

边坡中各因素与边坡稳定性的正负相关关系不同，应对各因素采用不同的归一化函数进行归一化。

正相关归一化函数为

(15)

式中：ximax，ximin为已知样本中各因素的最大值和最小值。

负相关归一化函数为

(16)

各个样本向量的归一化矩阵为R2。Uδ是样本xi对于各个聚类中心sh的相对距离矩阵。各类的聚类中心向量sh组成聚类中心矩阵S。

聚类中心向量由属于各类的样本向量通过式(15)和式(16)变换后，再求平均值得到聚类中心向量sh。

(17)

式中shi为各因素的聚类中心的值。

在得到各聚类中心向量后，用样本向量xω归一化后向量rω和聚类中心sh求得二者的广义欧式权距离[12]为

(18)

式中：d(rω,sh)为广义欧式权距离；rωi为归一化后样本中的各值；shi为各因素的聚类中心值。

求出rω对于各聚类中心向量的广义欧式权距离之和为：

(19)

式中d(rω,sk)为广义欧式权距离之和。

再求出样本向量xω对各个聚类中心向量的相对距离为

(20)

式中uωh为各样本对各个聚类中心向量的相对距离。

通过以上的运算，已经把所有边坡样本分成了c个类，其中边坡处在稳定状态中有c1个类，处在破坏状态有c2个类，即

c=c1+c2。

(21)

在运用最大隶属度原则进行分类时，当各隶属度相差较小时，可能会与实际情况产生较大偏差。因此在得到各个样本相对于各个聚类中心的相对距离后，基于离稳定类的聚类中心的相对距离越近越安全，离失稳类的聚类中心的相对距离越近越危险的原则，采用构建联系数向量[7-8]的方法替代最大隶属度原则来确定边坡状态。

根据联系数分量与样本相对于各个聚类中心的距离Uδ相乘得到的结果从而判断各边坡的具体归类情况。v为所有样本的聚类指标向量,即

v=EUδ。

(22)

式中E为联系数分量。

其中把[0,1]均分构建联系数分量[13-15]E，通过建立多元联系数再把所有的样本分散在(0,1)的c等分的区间上，同时由相似度评价指标δ，得到联系数评价指标，即破坏限i的公式为

(23)

当联系数vk≥i,k=1,2,…,n时，表示第k个边坡样本处于破坏状态。

4 实际计算

通过运用基于FAHP法和K-Means聚类的边坡稳定性模型对数据进行处理，之后用构建联系数向量的方法完成对未知边坡状态的评估和预测。

4.1 用FAHP计算各元素的权重

建立多人评价FAHP评价表，见表1。

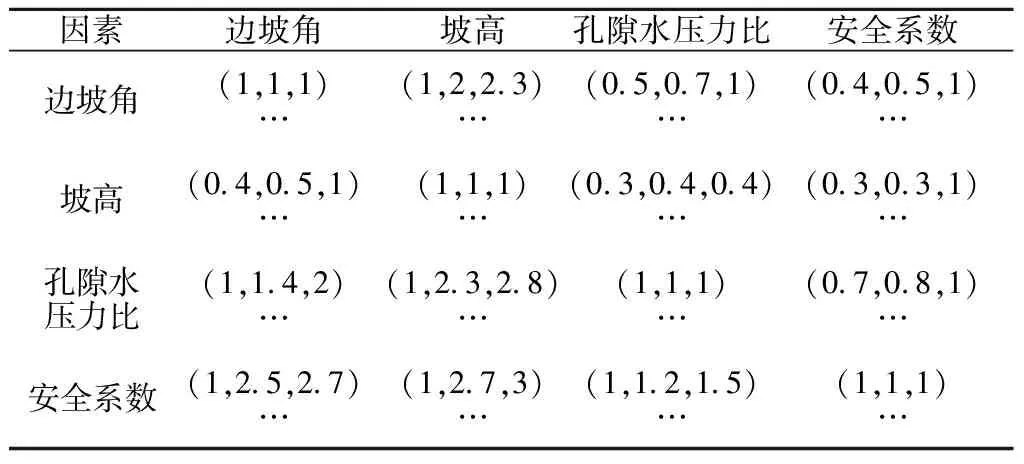
表1 FAHP评价表Table 1 Result of FAHP evaluation

注：为突出重点，其他的多组数据用省略号代替

同理求出D2,D3,D4，对求得的数据进行去模糊化计算。根据式(5)和式(6)可得

d1=min(D1≥D2,D3,D4)=0.47 。

同理求出d2,d3,d4,再对权重进行标准化，可得出w1为

同理求出w2,w3,w4。可得影响因素权重向量w为

w=(0.25,0.05,0.17,0.53) 。

4.2 基于样本进行分类

根据中交隧道局二公司近2 a来修建的项目采集20个边坡样本的原始数据，见表2。

取样本6作为xa，根据式(8)可以得到所有样本关于xa的隶属度矩阵为

表2 聚类边坡样本数据Table 2 Clustered slope samples

注：边坡稳定为0,破坏为1

把相对隶属度矩阵代入式(14)中，得到相似度向量Uε。令δ=0.75，则Uε中>0.75的样本和样本6视为一类。

首先把样本1、样本2 、样本7、样本8和样本6归为一类，再把样本1、样本2、样本6、样本7、样本8去掉后重新进行分类，重复该过程直到分类结束。这时把所有边坡样本划分成5类后，用式(15)和式(16)求出矩阵R2，然后通过式(17)求出聚类中心矩阵S,即

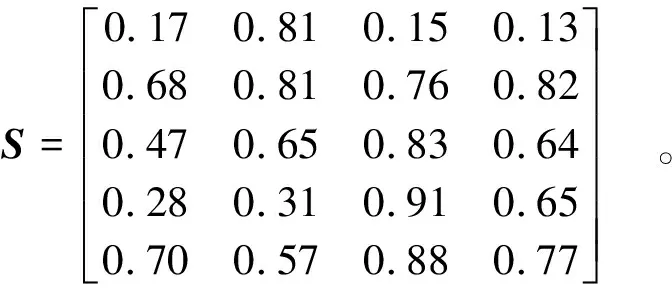
通过式(20)得到的相对距离矩阵为

在[0,1]之间根据聚类数c构建联系数分量E，E=(0,0.25,0.5,0.75,1)，再根据式(22)得到联系数向量v为

所有边坡样本已经分成5类，处于破坏状态有1个类别(c1)，处于稳定状态有4个类别(c2)，根据式(22)和式(23)，联系数评价指标i=0.6。把表2中的20个样本代入本文中的基于FAHP和K-Means聚类的边坡稳定性模型进行反演后，得到联系数向量v，把v中各元素与i进行比较可知：运用本文模型计算表2中的20个边坡样本，其中19个样本的计算结果与实际情况相同，正确率达到95%。

5 工程实际应用

新建南昌到赣州铁路客运专线高铁项目全程在江西省境内。工程地质条件为：剥蚀低丘，植被较发育，其地表水不发育，地下水多为孔隙水，主要接受大气降水，季节性明显。江西地区年平均降雨量1 635 mm左右，属于多雨地区。土质多为黏土土质、褐黄色、无不良地质作用。主要的土力学参数为：黏聚力c=30～35 kPa、内摩擦角φ=8.5°～18°、重度γ=18.93 kN/m3。

选取项目DK131+368.63—DK131+450.50段和DK88+18.24—DK88+97.32段的2个边坡样本对本模型进行实证研究。表3为赣昌客专工程边坡样本数据。

表3 赣昌客专工程边坡样本数据Table 3 Slopes samples of Nanchang-Ganzhouhigh-speed railway project

注：边坡稳定为0，破坏为1

由表3可知2#边坡在雨后发生了破坏。现就这两个样本进行计算验证。

利用式(15)和式(16)进行归一化，得到矩阵为

再运用式(20)求出R1中各个样本对于各类聚类中心向量的相对距离矩阵u为

得到样本距离各个聚类中心的相对距离后，根据稳定程度把[0,1]区间分成4等分，构建联系数分量E=(0,0.25,0.5,0.75,1)，而δ是聚类过程中的相似度评价指标，即δ=0.75。根据式(22)和式(23)，得出联系数向量v=[0.340 4,0.621 0]，再根据模型中联系数评价指标i=0.6和vk≥0.6则边坡破坏,可得出1#样本稳定、2#样本破坏的结论，与工程实际情况相吻合。