基于场应变的充填体与围岩组合模型循环加卸载试验研究
2019-01-21,,
, ,
(1.华北理工大学 矿业工程学院,河北 唐山 063009;2. 华北理工大学 河北省矿业开发与安全工程实验室,河北 唐山 063009 )
1 研究背景
工程岩体在矿山开采作业中处于不断的动态扰动过程中,每次开采导致的岩体扰动都会引起其应力状态重新分布,导致工程岩体处于反复加卸载状态。实时监测处于反复加卸载状态下的岩体变形情况具有重要的工程实际意义,因此研究循环加卸载条件下的充填体与围岩相互作用机理具有重要实际意义。
当前,充填采矿方法在矿山开采工程中被广泛应用,众多学者也从不同的角度就充填体对围岩的力学作用机理进行了深入的探索,并提出了多种力学作用机理。Yamaguchi等[1]认为,随着周围岩体的变形程度增大,充填体开始发挥支护作用,即使充填体被充分压缩,对于围岩的移动变形还是会起到很大制约作用,而非只起到对围岩的支护作用;岩体由于变形破坏产生的裂隙和塑性变形致使体积膨胀,会出现新的压力拱。蔡嗣经等[2]根据充填体与围岩的相互作用机理采用Drucker-Prager强度准则确立了充填体-围岩的力学模型。秦帅等[3]、彭志华[4]通过试验研究,进一步论证了充填体的应力吸收与应力转移、应力隔离、被动支撑等作用。Liu等[5]探讨了不同灰砂比充填体的破坏机理及充填体与围岩的相互作用机理。Xue等[6]为确定最佳的沿空留巷宽度,利用数值模拟等方法研究了不同充填宽度下巷道围岩变形破坏机理。马小亮等[7]、吴彬等[8]研究了在循环加卸载过程中不同侧应力和不同应变速率下的混凝土的损伤规律。赵星光等[9]、焦贵德等[10]、赵闯等[11]分析了不同种类岩石在循环加卸载过程中的破坏规律。
传统方法布设应变片监测的是埋设区域的局部应变,对于全场变形的测量还存在一定的缺陷。全场应变仪则能够进行高精度的非接触全场应变监测,故作为一种新型监测手段被众多学者用于监测岩石受压过程中的变形场情况。米红林[12]利用电阻应变计验证了数字散斑相关测量技术,能够用于岩石等材料的形变检测、预报变形信息,其结果可以定量和定性显示。郭文婧等[13]基于数字散斑相关方法开发了一种虚拟引伸计测量方法,并通过实验验证了虚拟引伸计的可靠性。彭瑞东等[14]将亚像素插值和相关系数插值相结合,有效提升了数字散斑相关法的搜索效率和计算精度,并通过自行研发的数字散斑相关方法程序实现了岩石SEM图像中微小变形的分析计算。宋义敏等[15]采用白光数字散斑相关方法作为实验的观察手段,对单轴压缩条件下岩石变形破坏进行了研究。
尽管近年来国内外的学者对充填体与围岩的破裂机理进行了大量的研究,获得了很多有意义的结果,但这些结果主要是针对充填体的作用以及在额定荷载下充填体与围岩相互作用,对于多次扰动下的充填体与围岩相互作用机理研究不够充分。本文采用VIC-3D非接触全场应变仪对循环加卸载过程中组合模型的应变同步监测,通过分析试验中的应力-应变曲线以及场应变演变情况,对组合模型的裂隙演变规律进行探索,以揭示循环加卸载条件下充填体与围岩相互作用机理。

图1 组合模型示意图Fig.1 Schematic diagram of combined model of surrounding rock and mining stope
2 充填体与围岩组合模型加卸载试验
2.1 试样制备与试验方法
根据充填采矿法的原理,设计了如图1所示的组合模型,立方体岩石试块尺寸为150 mm×150 mm×150 mm,在立方体试块中心开挖Φ50 mm×150 mm的圆柱孔洞模拟采场并充填。为了研究不同种类岩石的影响,围岩采用大理岩、花岗岩、玄武岩3种岩石来模拟。
在立方体试块孔中灌注质量浓度为70%、灰砂比为1∶8的充填体,形成围岩与充填体组合模型。在温度20℃和湿度95%条件下将组合模型养护28 d,达到养护龄期后开始加卸载试验。
在试验过程中将侧向压力设为恒定荷载,模拟矿山应力条件,选取5,10,15 MPa 3种不同侧压力;轴向采用速率为0.2 mm/min的位移控制方式进行逐级加卸载。循环上限应力初始值为20 MPa,以20 MPa为梯度逐级增加上限应力进行加卸载试验,至试件达到峰值强度而破坏;在实际工程中,充填体与围岩是存在于一定压应力下,因此每次卸载到抗压强度的5%左右,轴向下限应力设为5 MPa。每种岩石每种侧压力情况重复进行5次试验,共计进行了45次组合模型试验。同时,为了比较,每种岩石还进行了未充填围岩模型试验。
2.2 试验设备及装置
本次试验采用RLW-3000微机控制剪切蠕变试验机对充填体与围岩组合模型进行双轴加载,使用美国CSI公司生产的VIC-3D非接触全场应变仪监测组合模型的轴向应变、横向应变,试验设备如图2。在本次试验中,为了便于观测,区域选择前端面进行研究,除去试验中仪器所占位置,以菱形区域为研究对象。VIC-3D非接触全场应变测量系统采用优化的3D影像相关算法,根据数字图像相关方法对被测对象变形前后散斑场进行采集并转成数字散斑场进而计算,获取被测对象表面应变分布情况,其测量精度可达±0.015%,能够清晰发现临界破坏点。

图2 RLW-3000试验机及全场应变仪Fig.2 RLW-3000 testing machine and full-field strain gauge
3 试验结果与分析
3.1 不同侧压力下组合模型循环加卸载应力-应变曲线特征
组合模型轴向应变和横向应变数值通过全场应变仪在所选观测区应变场进行平均获得,体积应变通过计算获得。以大理岩为例,进行了以5,10,15 MPa 3种不同侧压条件下组合模型轴向应变、横向应变及体积应变与应力关系的试验结果分析,并绘制组合模型在循环加卸载破坏过程中的应力-应变关系曲线,如图3所示。
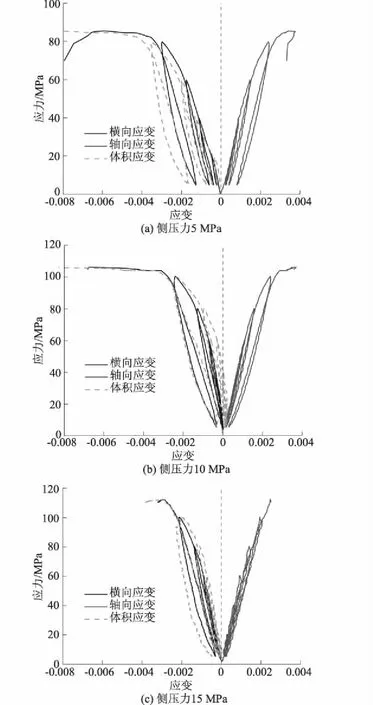
图3 不同侧压下大理岩应力-应变曲线Fig.3 Stress-strain curves of marble under different lateral pressures
由图3可以看出:3种侧压下的加载与卸载曲线均不重合,每个加卸载循环都会生成一个塑性滞回环;随着循环的增加,塑性滞回环慢慢向两侧移动,破坏变形量的发展速度逐渐加快,累积变形量不断增大,滞回环面积逐渐增大。这是由于在前几个循环应力水平比较低时,岩石变形主要方式为线弹性变形;进入第3个循环以后,应力卸载点超过了岩石的屈服点,岩样内部较软区域最先开始出现屈服弱化现象;随着荷载的增大,屈服范围不断扩大,致使不可逆塑性变形逐渐增大。不同侧压力下的每个循环中卸载后留下的塑性变形也有不同,应力-应变滞回环在由加载转为卸载时刻是尖叶状,而非椭圆形,表明岩石的弹性变形响应迅速,塑性变形小。
根据线应变与体积应变关系,绘出不同侧压下的大理石组合模型体积应力应变曲线(见图3)。其中横坐标正数代表试件受压体积变小阶段,出现这一过程主要是由于在较大的侧压存在情况下,试件内部最初的裂隙在轴向加压时逐渐压实导致试件体积减小,如图3(b)和图3(c);负数代表试件体积增大阶段,这是因为随着循环加卸载过程中荷载的增加使得试件横向应变逐渐增大,导致试件内部裂隙扩张,出现扩容现象。因此大理岩的破裂经历了一个扩容的过程。
为研究侧压力对组合模型强度的影响,统计了不同侧压力下轴向应力峰值,如表1。

表1 不同侧压下组合模型轴向应力破坏峰值Table 1 Peak values of axial stress at failure of combinedmodel under different lateral pressures
分析表1可知:随着侧压力值增加试样破坏峰值强度增大,表明侧压阻碍了试样的破坏和裂隙的滑移,提高了试样的抗压强度,并且侧压越大,滞回环越密集,岩石的残余应变越小。究其原因为试样屈服产生裂隙后,在卸载过程中,侧压力能够促使原有裂隙闭合,阻碍裂隙滑移,侧压力增高时裂隙闭合更加充分,试样的变形减小,从而具有较高的弹性模量,表现出试样抗变形能力随侧压力的增大而逐步提高。
3.2 同一侧压力下不同种类岩石组合模型加卸载应力-应变曲线特征
以侧压5 MPa条件下的组合模型为例,开展了大理岩、花岗岩、玄武岩3种不同围岩组合模型轴向张拉应变以及横向应变与应力关系的试验研究,获得组合模型在破坏过程中的应力-应变关系曲线,如图4所示。

图4 不同组合模型的应力-应变曲线Fig.4 Stress-strain curves of combined models with three different rock types
根据图4中的3种组合模型在5 MPa侧压下曲线可以看出:
(1)横向应力-应变曲线在每次加载与卸载过程中均不重合,每次加载与卸载曲线都会构成一个塑性滞回环,而且滞回环的面积随加卸载循环的增多而不断增大。其中,大理岩滞回环分布稀疏,存在较大塑性变形;玄武岩的滞回环最密集,各滞回环几乎重合,接近线弹性;花岗岩介于二者之中。
(2)大理岩轴向应力-应变曲线中加载与卸载曲线不重合,存在显著塑性滞回环;花岗岩与玄武岩几乎重合,没有明显的塑性滞回环,其变形主要为弹性变形,几乎没有残余变形。造成这种现象的原因是大理岩的塑性比较好,而花岗岩和玄武岩比较致密坚硬,不易产生残余应变。
4 不同围岩加卸载破裂应变场演变规律
为了研究组合模型在加卸载破裂过程中的应变场演变规律,进一步分析充填体与围岩相互作用的破裂机理。本文研究了不同侧向应力条件下大理岩、花岗岩、玄武岩3种不同围岩组合模型x方向的应变场,获得组合模型在加、卸载破坏阶段的x方向应变场序列图像,以exx表示x方向应变,正数表示拉伸,负数表示压缩。
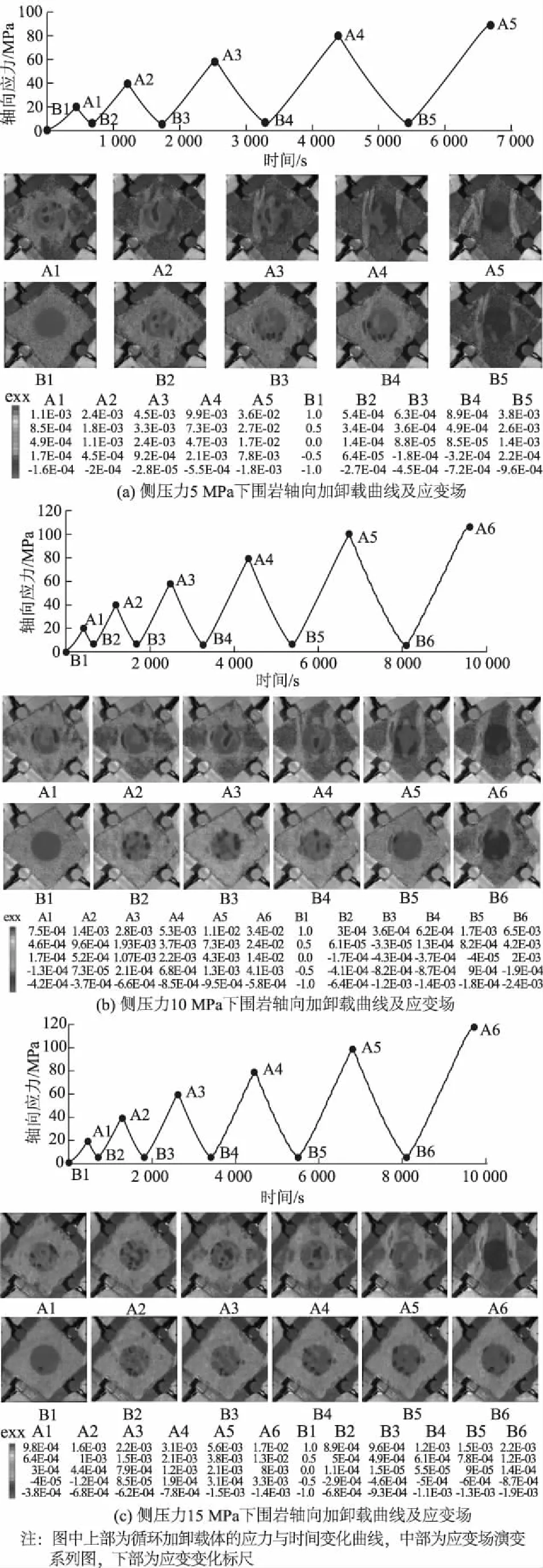
图5 大理岩应变场序列演变过程Fig.5 Strain field of marble under different lateral pressures
4.1 不同侧压力下围岩破裂应变场演变规律
图5为大理岩应变场序列演变过程。由图5(a)大理岩的x方向应变场演化过程可以看出:试验开始前σ=0(t=0 s)时,试样x方向应变都为0;第1个循环内,整个试样只有充填体上局部有张拉应变区出现,面积比较小并且为随机分布,没有形成条带区域;第2个循环加载至上限应力σ=40 MPa(t=1 212 s)时,在充填体的中心有一条明显的张拉应变区,此时充填体被横向拉伸,卸载至下限应力σ=5 MPa(t=1 728 s)时,应变又重新随机分布;第3个循环加载至上限应力σ=60 MPa(t=2 538 s)时,充填体中心的张拉应变区上下延伸至围岩内,充填体左侧围岩也产生了一条竖向裂纹,卸载至下限应力σ=5 MPa(t=3 361 s)时,在左侧围岩上仍能看出张拉应变区,说明存在残余应变,该阶段试样已经进入屈服阶段;第4个循环加载至上限应力σ=80 MPa(t=4 388 s)时,充填体右侧围岩上也产生了张拉应变区,且几乎与左侧的竖向区域平行,此时充填体上的张拉应变区应变值减小,卸载至下限应力σ=5 MPa(t=5 442 s),左右围岩均存在残余应变;第5个循环加载至σ=86 MPa(t=6 772 s),试样破坏,充填体中心的竖向裂纹闭合,左右两侧围岩上张拉应变区面积增大,围岩左侧裂纹的上部应变值大于下部应变值,主裂纹上形成一条分支裂纹,围岩右侧裂纹的下部应变值大于上部应变值。
同样分析10 MPa和15 MPa 2种侧压力条件下大理岩应变场演变也有类似规律。综合分析3种不同侧压力下的大理岩应变场图像可知:张拉裂隙均主要产生在采场两侧围岩中,基本呈对称分布。在围岩中首次出现明显条带张拉应变的时刻分别为:侧压5 MPa下的第3个循环且上限应力峰值σ=60 MPa(t=2 538 s)、侧压10 MPa下的的第4个循环且上限应力峰值σ=80 MPa(t=4 342 s)、侧压15 MPa下的第5个循环且应力峰值σ=100 MPa(t=6 810 s)。随着侧压力值的增大,围岩最大应变值逐渐减小,侧压力为5 MPa时围岩最大应变值为3.6×10-2,10 MPa时为3.4×10-2,15 MPa时则为1.7×10-2。即侧压力的增大延迟了两侧围岩张拉应变的发生,对应循环荷载下的张拉应变值也有所降低,减缓了张拉破坏的出现。
4.2 不同种类围岩破裂应变场演变规律
在不同种类围岩中,应变场变化也表现出一定的差异性。图6为侧压力5 MPa条件下不同围岩应变场演变过程。

图6 不同种类围岩应变场变化Fig.6 Strain field variation of different types of surrounding rock
由图6(a)试验中花岗岩x方向应变场演变过程可以看出:该演变过程与大理岩的演变过程类似,第1个加卸载循环内张拉应变区是随机分布;第2个循环和第3个循环每次加载至上限应力时充填体中心都产生了张拉应变区,并随着加卸载次数的增多而增大,每次卸载至下限应力时应变重新分布;第4个循环加载至上限应力σ=80 MPa(t=4 688 s)时,充填体中心的张拉应变区增大,程度变深,延伸至围岩,并且充填体两帮的上下侧均产生了一条张拉应变区,如图6(a)中黄色圆圈标注区域;第5个循环加载至上限应力σ=100 MPa(t=7 398 s)时,充填体两帮上下侧的张拉应变区各自连接,最终演变为3条并列条带状张拉应变带;第6个循环加载至σ=118 MPa(t=10 428 s) 时,在第5个循环中出现的3条张拉应变集中带相互影响和“竞争”,最终两侧围岩内的2条占优,中间充填体内的应变集中条带被“淡化”。
由图6(b)的x方向应变场演变过程可以看出:第1个循环加载至上限应力时,充填体左侧有条带状的张拉应变区;第2个循环加载至上限应力时,充填体右侧和上下方也出现张拉应变区,表现为充填体周围环形的张拉应变区以及充填体正上方、正下方条带状的张拉应变区;第3个循环加载至上限应力时,前一个循环出现的环状以及条带状张拉应变区面积增大、程度加深;第4个循环加载至上限应力时,除之前充填体周围的环状张拉应变区以及充填体正上、下方的条带区域以外,左上方、右上方围岩也出现了竖向条带状的张拉应变区;第5个循环以及第6个循环加载至上限应力时,之前出现的张拉应变区继续增大;自第3个循环卸载至下限应力开始试样出现残余变形,表明此循环开始试样内部较软区域最先出现屈服弱化现象。
综合分析可见:加载期间,采场两侧围岩张应变增大,呈张裂趋势;卸载期间,上个循环的张应变减小,呈裂隙闭合趋势,但仍残存张应变。随循环次数增加,加载产生的张应变逐渐扩大,张裂条带向上下扩展,而卸载残余张裂也逐渐扩大。循环加卸载过程中,应变场演变特征是:初期荷载较小时表现为应变值随机分布的近似均匀场,随荷载增大应变场从均匀场向非均匀场转变,形成应变集中条带,而不同荷载卸载后应变场又趋于近似均匀场。张裂破坏空间的变化一般规律是:张裂首先出现于充填体中,随循环荷载增大,充填体破裂承载力下降,张裂向两侧围岩中转移,由此可认为,充填体与围岩在循环加卸载作用下并非同步变形、同步承载,具有时空与破坏形式差异。随岩石种类大理岩、花岗岩、玄武岩变化次序,脆弹性增强,破坏形式具有从双裂隙向单裂隙转变,且张裂隙增大趋势。
5 组合模型破裂机理分析
5.1 充填采场围岩破裂形式
为研究充填体对组合模型强度性能及破裂机理的影响,开展对比试验,以侧压力5 MPa为例进行分析。表2为3种岩石未充填、充填试样的破坏形式。
对于未充填的试样,垂直应力向模拟采场两侧转移,两侧承载应力,形成应力集中,在加卸载后期较高应力时两帮出现强烈的岩爆现象,大理岩和花岗岩的岩爆剥离岩量较多,而玄武岩只是局部岩爆剥离。随着应力的进一步增大,大理岩、花岗岩以岩爆位置为起点形成宏观剪切裂纹,而玄武岩则未出现显著裂纹。
根据应变场规律可知,组合模型的破坏形式主要为形成2条与中心充填体圆柱相切的张拉应变区域。分析其原因为充填体对于围岩起到了支撑作用,弱化了两侧围岩的应力集中现象,将模型整体划分为2类区域,如图7。相较于两帮即Ⅱ区而言,中心带即Ⅰ区的支护能力要弱且弹性模量比Ⅱ区低,因此在相同的荷载作用下,Ⅰ区的变形量更大,在Ⅰ区和Ⅱ区的交界面上剪应力较集中,存在剪切应变。由于大理岩和花岗岩的塑性较好,其组合模型最终破坏形式为剪切破坏;而玄武岩由于脆性较大,在循环加卸载过程中采场顶底板出现张拉破坏,形成一条垂直的“I”字形破坏带。

表2 不同种类围岩破坏形式Table 2 Failure modes of different types ofsurrounding rock

图7 组合模型破裂应变分区示意图Fig.7 Zoning of the combined model according to strain at failure
5.2 充填采场围岩破裂机理分析
巷道开挖后初始的应力平衡遭到破坏,会出现新的围岩应力即“二次应力”,进而导致巷道围岩中出现一个应力变化区域,出现应力集中。当圆形巷道开挖后,开掘空间无任何人工支护结构时,圆形巷道周边不会出现拉应力的条件是1/3≤λ≤3,其中,λ=q/p,λ为侧压力系数;q为围岩水平应力;p为围岩垂直应力。当λ<1/3时,围岩顶板表现为拉应力;当λ>3时,两帮则出现拉应力。根据不同围岩组合模型在出现明显张拉应变时刻的垂直应力值计算所得λ值(取整分数)如表3所示。

表3 不同组合模型的侧压系数Table 3 Lateral pressure coefficient of differentcombined models
由表3可知,不同围岩的组合模型的侧压力系数均远<1/3,分析原因为充填体对围岩形成支护反力作用,导致围岩出现张拉应变所需的垂直应力值增大,由于充填体充填固结过程中存在收缩,造成与围岩不完全接触,随着荷载的增加组合模型中充填体与围岩剥离。对于在整体结构岩体掘进的巷道,其周边岩体破坏的形式主要有2种:①x型剪切裂缝;②张开裂缝。根据塑性滑移线理论可知:不同种类的岩石破坏形式不同,软性岩石出现剪切破坏。如表2中的图片所示,大理岩左侧出现剪切破坏;对于坚硬岩石则会出现拉伸破坏,玄武岩充填体顶部出现张开裂缝。
6 结 论
(1)在循环加卸载过程中3种岩石组合模型均具有很好的记忆特性;组合模型的破裂经过一个扩容过程,不可逆塑性变形随加卸载次数增加逐渐增大。
(2)强度较低的充填体最先出现竖直条带状张拉应变集中区域,并延伸至上下方的围岩中;随着荷载的增大,张拉应变区由充填体逐渐向围岩两帮移动。充填体与围岩变形具有时空非同步性与破坏形式差异。
(3)充填体能够增强围岩的整体性,减弱采场两侧围岩的应力集中,提高围岩的抗压强度。
(4)应变场随循环加卸载演变具有从初期的近似均匀场向非均匀场转变趋势,呈现应变局部化特征。随侧压力增大,围岩张拉破坏呈减缓趋势。
(5)在循环加卸载过程中,不同种类围岩的组合模型破坏形式不同:围岩强度较弱的组合模型出现剪切破坏,围岩强度大的组合模型则会出现拉伸破坏。
