包气带水分迁移离心模拟的可行性探讨

2019-01-21

长江科学院院报 2019年1期

(东华理工大学核资源与环境国家重点实验室，南昌 330013)

1 研究背景

包气带作为联系“四水”(大气水、地表水、包气带水和地下水)动态水循环系统的纽带，是指从地下潜水面向上延伸至地面的地带[1-2]，是大气水和地表水同地下水发生联系并进行水分交换的地带，由于污染物大多是随水扩散发生迁移，因此它也是地表污染物向下迁移污染地下水的通道[3]。近年来，人类活动的影响及各种污染物的排放，加剧了土壤的污染，土壤退化、地下水污染、荒漠化、地面沉降等一系列环境问题都与包气带土壤水分有密切联系[4]。由于包气带在水文循环中处于重要位置，与降水入渗、地表蒸发、地下水补给、潜水蒸发等水文过程密切相关，同时，包气带水分运动是污染物运移及水、汽、热运动的主要驱动力，因此，对包气带中水分的迁移进行研究，探明水分运动规律，对于研究“四水”转换、地下水来源、水资源开发利用、生态保护及人类的生产生活都具有十分重要的意义[2,4-5]。

离心模拟是将按比例缩小尺寸的原型放在离心机内，通过离心加速还原原型中应力水平并开展模型模拟的一种技术[6-7]。离心模拟通过加速水分和溶质在土壤中的迁移速度，能够大大缩短实验时间[8]。相比于常规物理模拟方法，离心模拟具有快速搜集实验数据、应力水平保持和原型一致、预测全尺度的迁移行为和可以开展二、三维模拟等优点[6,9]。离心模拟技术已经广泛应用于包气带溶质迁移的研究[8,10-13]，在低渗透土壤长期污染物迁移及获取数据验证模型等方面具有重要意义。然而，对于离心模拟技术能否应用于包气带水分迁移尚存争议[6,14]。Goforth[15]和Poulose等[16]对该技术应用于包气带水分迁移表示怀疑，他们认为，在饱和度较低的土中，离心机不能正确模拟基质势作用下的流体流动。Mitchell[17-18]认为离心模拟能够正确描绘原型污染物迁移现象，包括非饱和细砂土中基质吸力引起的迁移。

水力传导系数与含水率的关系K(θ)及土水特征曲线SWRC(Soil Water Retention Curve)对于理解包气带水分的存储及迁移具有重要意义，常规方法确定K(θ)和SWRC存在许多挑战，最主要的挑战是实验耗时过长，因此大多数包气带水分迁移研究都是依靠经验公式或理论模型。现有研究表明，纯粹依靠经验关系或理论模型并不可靠，通过实验获取非饱和土水力特性十分重要。Singh等[19]利用离心机测定了多种不饱和土的水力传导系数及其特征曲线，发现与理论值很接近。

目前，离心模拟技术在包气带溶质迁移的应用中都默认了该技术能够成功模拟包气带水分迁移。上述争议无疑会阻碍离心模拟技术的推广和发展，然而目前并没有相应的研究来解决这一争议。本文通过建立离心场内包气带水分迁移的一维理论模型和数值模型，选用4套文献数据对数值模型进行验证，在此基础上探讨离心模拟技术应用于包气带水分迁移研究的可行性，期望从理论上对该争议的澄清进行探讨。

2 包气带水分迁移离心模型

离心模型中非饱和水流是受水势梯度驱动的，其控制方程为Richards方程。由于离心模型处于离心力场内，故离心条件下包气带水分迁移的控制方程形式不同于自然重力下常规的情况。

2.1 理论模型

2.1.1 水势与达西定律

图1是一维离心模型中非饱和水流的原理分析图，其中rt表示模型顶部半径；rb表示模型底部半径；z表示当前位置离参照面的距离；L表示离心模型的高度。驱动水流运动的水势主要有水的位置势能、动能和基质势能3部分。

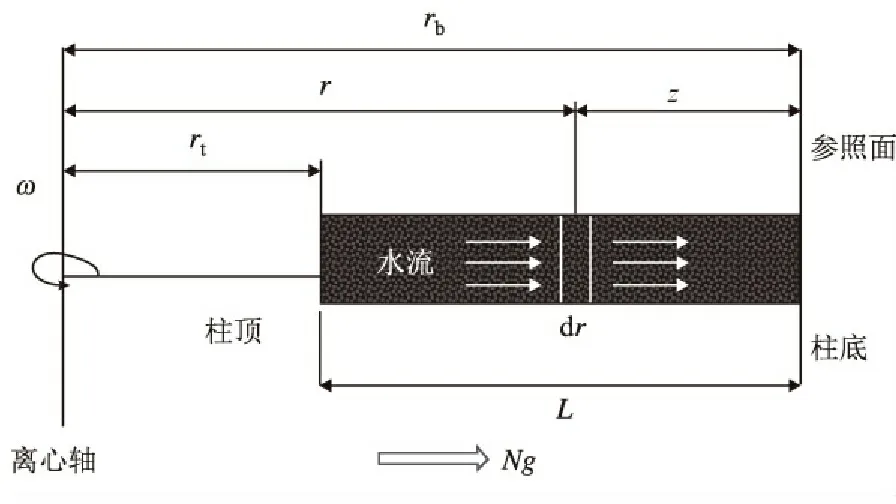
图1 水分迁移一维离心模型分析图Fig.1 Analysis of one-dimensional water migration centrifugal model

离心模型中水分的渗流速度一般来说很小，水的动能可忽略不计，离心模型中单位质量水的水势能为

Φ=Pe+ψm/ρ。

(1)

式中：Φ为水的势能；Pe为离心状态的水的位置势能；ψ是基质吸力；ρ是水的密度；下标m代表离心模型。

离心状态下和常规情况下水的势能的主要差别在于位置势能的计算不同。离心加速度沿径向存在一个分布趋势而不是某个固定值，其大小是半径和角速度的函数(a=rω2)。离心状态下水的位置势能等于将单位质量的水从参照面移至当前位置需克服离心力所做的功，将模型底部设为参照面，则半径r处单位质量水的离心位置势能为

式中：a为离心加速度；ω为角速度。

联合式(1)和式(2)可得一维离心模型非饱和水的势能为

(3)

达西定律描述了水流运动和水势梯度之间的关系，离心情况下达西定律的适用性已被许多研究证实[8,13]，其表达式为

(4)

(5)

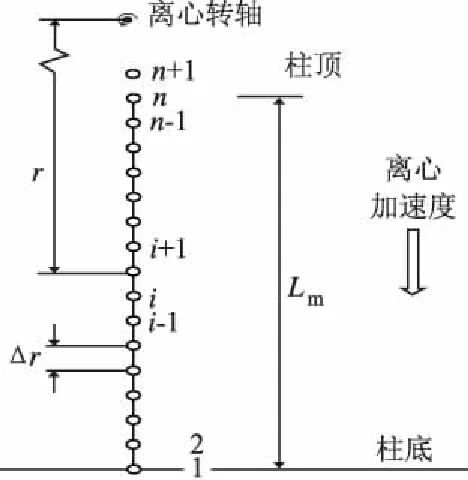
图2 一维离心模拟的节点剖分 Fig.2 Node dissection of the one-dimensional centrifugal modeling

2.1.2 Richards方程

考虑离心模型中某一个控制体积单元(图1)，根据连续性原理有(t为离心模拟时间；θm是离心状态下的含水率)

(6)

将式(5)代入式(6)可得

式(7)是包气带水流的控制方程，它刻画了离心场内水流流经非饱和土壤的过程规律。

2.2 数值模型

2.2.1 模型数值化

用n个节点将一维离心模型分成n个有限差分网格(图2)，图中第n+1个节点是虚拟节点，是为了在求解中刻画离心模型顶部边界条件所设。对于模型中第i个节点，利用改进的Picard循环[20]线性化式(7)中的非线性项，则等号后面项的有限差分近似为

(8)

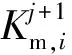
对时间项欧拉形式向后差分，并嵌入Picard循环(Δt为时间步长)得

(9)

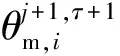
定义土壤的特殊水容量为

(11)

联合式(9)—式(11)，则式(7)有限差分为

联立式(8)和式(12)，将未知项放在左边，已知项放在右边，则第j+1个时间步、τ+1个Picard循环中基质吸力可通过式(13)求得,即

(13)

将式(13)应用于离心模型上所有节点，得到一个方程组，可用追赶法求解。对于边界节点，式(13)需要调整以反映不同的边界条件。

2.2.2 边界条件和物料守恒

根据文献[20]，数值模拟时底部的自由流边界可处理成定水头边界。因此，本文考虑的边界条件为：模型顶部提供一个稳定通量的水流，底部是一个定基质吸力边界，即

(14)

式中：qb是顶部的水流通量；ψb是底部稳定的基质吸力。

为了了解一维离心模型中非饱和水流的物料守恒情况，需要知道上下边界的水流通量和模型中含水率的变化。模型底部的出流水通量可以利用泰勒级数推导而出，即

(16)

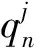
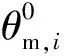
表1 例1—例4数值模拟参数取值Table 1 Parameter values of examples 1-4 in numerical modeling

注：†表示文献中没有直接给出而是从文献的图表中获取的参数；表示原文献该实验重复了2次，表中所给数据为2次实验的平均值

2.2.3 土壤水力学特性

求解Richards方程要知道水力传导系数和基质吸力、含水率和基质吸力之间的关系[21]，即渗透率函数K(θ)和土水特征曲线SWRC。常用Van Genuchten模型[22]描述SWRC，即

(18)

式中：Θ是有效饱和度；α，nv，mv=1-(1/nv)是Van Genuchten模型参数；θs和θr分别为饱和含水率和残余含水率；h是压力水头，可用h=ψ/(ρg)实现和基质吸力的转换。

K(θ)有许多种形式，其中Gardner模型[23]和Mualem模型[24]是最常用的，即：

(19)

(20)

式中：Ks是土壤的饱和水力传导系数；ψo和β是Gardner模型参数；l是孔隙连通性参数，对大部分土壤来说为0.5[24]。

3 包气带水分迁移离心模拟可行性探讨

3.1 文献数据的验证

非饱和水分迁移离心数值模型用4套已发表的文献数据(表1)进行验证，参数取值均从文献中获取(有些通过图表获取实验数据，再利用Solver求解器间接拟合得到)。

3.1.1 例1：ω=0时基质吸力主导的非饱和水流

当没有角速度时，离心加速度为0，非饱和水的位置势能处处相等，水流运动受基质吸力梯度主导。本套数据来自Kirkham[25]，使用一根总长25 cm由透明有机玻璃制作的水平土柱开展实验，整根土柱填满红色Ferrosol土，填充重度为0.155 g/cm3。土柱一端连接一个马氏瓶，另外一端保持开放暴露在空气中。由于实验是破坏性取样，为了获得一个时间系列的数据共做了6次实验，初始和边界条件不能完全相同，本文采用6次实验初始和边界条件的平均值作为参数输入，并将连接马氏瓶的一端处理成固定基质吸力为0 kPa的边界条件，另外一端处理成自由流边界。模拟结果和实验数据对比(图3)说明两者匹配较好。

图3 水平土柱实验基质吸力梯度主导的非饱和水流实验数据[25]和模拟结果的对比Fig.3 Comparison between the experimental data ofunsaturated flow dominated by matrix suction gradient andthe simulated results in horizontal soil column experiment

3.1.2 例2：稳态流离心模型剖面水分曲线

本套数据来自Nimmo等[26]，用来验证本文提出的理论模型在预测稳态模型剖面上水分分布曲线方面的能力。实验过程中土柱部分内填充Oakley砂，预先用脱气的0.01N CaSO4和0.01N CaSeO4混合液饱和，在100 rad/s(对应离心加速度约194g)的角速度下离心。离心过程中顶部提供稳定的水流通量，底部维持固定基质吸力为-10 kPa的边界条件。离心稳定至没有水分出流后，土样被切成1.25 mm厚的片测定不同部位的含水率。此处利用数值模型根据其实验状态来预测稳态剖面的水分分布情况，模拟结果和实验数据对比如图4(a)，可以看到两者相当吻合。图4(b)是预测的基质吸力分布曲线，从中可以看出当稳态建立后，靠近离心模型顶部的水分及基质吸力分布趋近均一，重力水平N值越大现象越明显[20]。

图4 稳态剖面曲线Fig.4 Numerical simulation of the steady-state profile curve

3.1.3 例3：暂态非饱和水流

本套数据来源于Nakajima等[27]，他们使用一台半径2 m、安装有基质势传感器且能够测量累计出流量的土工离心机开展实验，拟利用一步出流法估算非饱和土的特性参数。离心过程中土样顶部水流通量为0 m/s，底部保持和水面的接触(可视作固定基质吸力为0 kPa的边界条件)。实验使用了10，20，40g的离心条件，但调整了模型的尺寸，保证了模拟的是同一个原型。Nakajima等[27]利用获得的实验数据估算了非饱和土特性参数，本文利用他们估算的实验参数逆向模拟暂态的非饱和水分迁移过程。图5对比了模拟结果和实验数据，两者有着较为满意的吻合度。40g条件下匹配较差的原因有2个：不理想的边界条件控制和基质吸力传感器(张力计)性能限制。从图5可以看到在原型时间为80 min时，土样底部的基质吸力水头为正值，表明土样底部排水不畅甚至发生了积水现象。此外，重力水平N较大的情况下，会引起快速的孔隙水压变化，会对张力计的陶瓷头产生破坏从而引起读数不准。

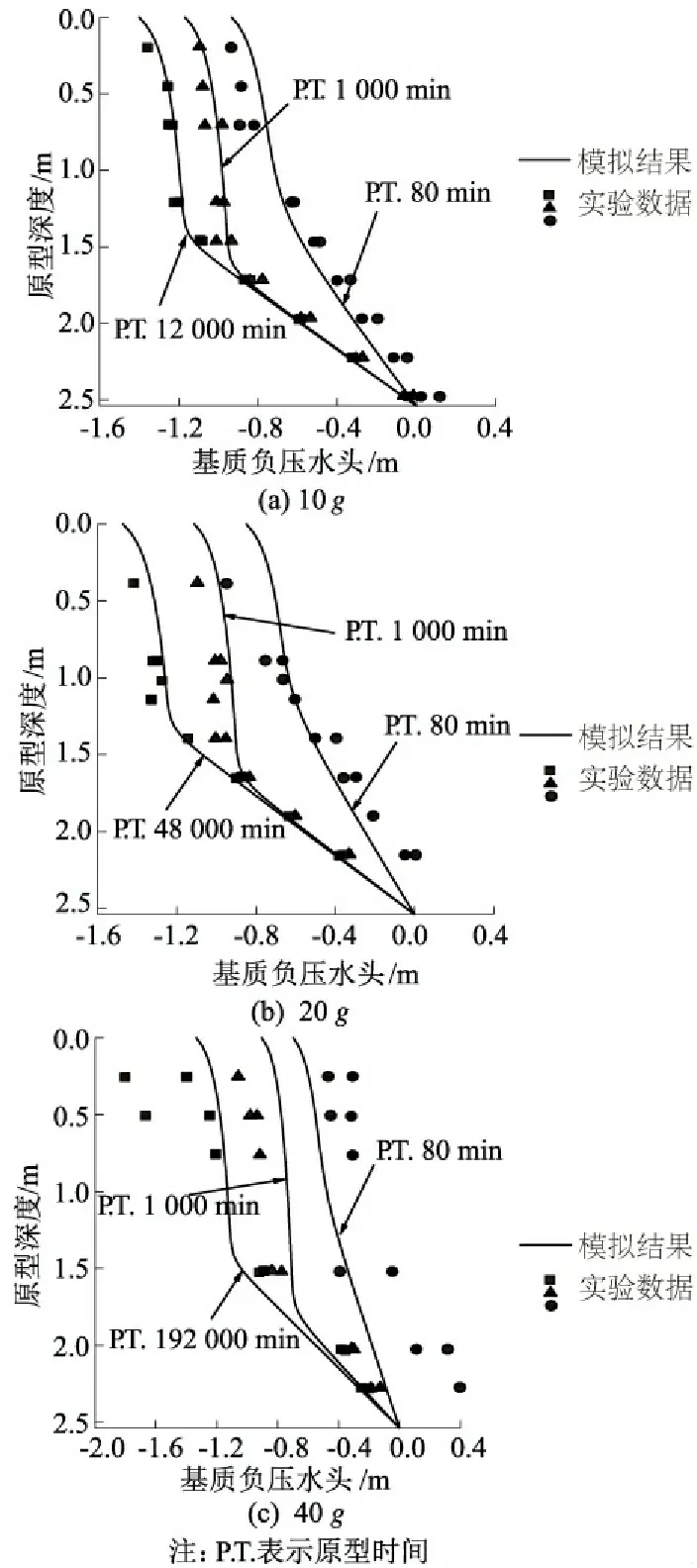
图5 数值模拟结果和实验数据对比Fig.5 Comparison between numerical simulation resultsand experimental data

3.1.4 例4：多重转速离心实验非饱和水流

表2 Run 1的离心转速改变时间序列Table 2 Time series of the centrifugal speed changes in Run 1

土样底部的固定基质吸力在一次多重转速离心实验中并不是全程不变的，每改变一次离心转速，该值就相应改变一次。本文假设多孔陶瓷片在离心过程中每一处的水势相等，土样底部的固定基质吸力可通过式(21)计算。

(21)

式中H为陶瓷片的厚度。利用数值模型预测了Run 1实验过程中的水分迁移变化并和实验数据比较(图6(a))，模拟结果和实验数据很吻合。此外，本文还预测了在每个转速改变时间的节点上，土样的基质吸力剖面分布曲线(图6(b))，和等[28]给出的完全一致，进一步说明了理论模型的正确性。

以上4个不同场景的实验可以充分验证理论及数值模型的正确性，但仍不足表明数值模型能够正确预测离心非饱和流。以例1为例，结合式(17)考察数值模型的物料守恒特性，结果如图7所示。本文将物料守恒误差在5%内视为优秀，根据图7可知当时间步长和空间步长均足够小时，数值模型的物料守恒特性优秀。此外，数值模型对空间步长比时间步长更敏感：当时间步长从1 s跨越到60 s时，96 min时刻的非饱和水分迁移的物料误差均在5%以内；当空间步分别长为2.5 mm和5 mm时，物料误差分别达到并超过了10%和60%。因此，当利用数值模型时，建议使用适当的时间步长提高计算效率，使用较小的空间步长保证模拟的质量。要强调的是情景1不是处在离心场内，而在离心场下应当使用更小的空间步长，尤其是靠近底部出流边界处的空间步长更应如此[28]。

图6 Run 1实验模型预测结果和实验数据对比及土样基质吸力剖面分布曲线Fig.6 Comparison between experimental model prediction results and experimental data in Run 1

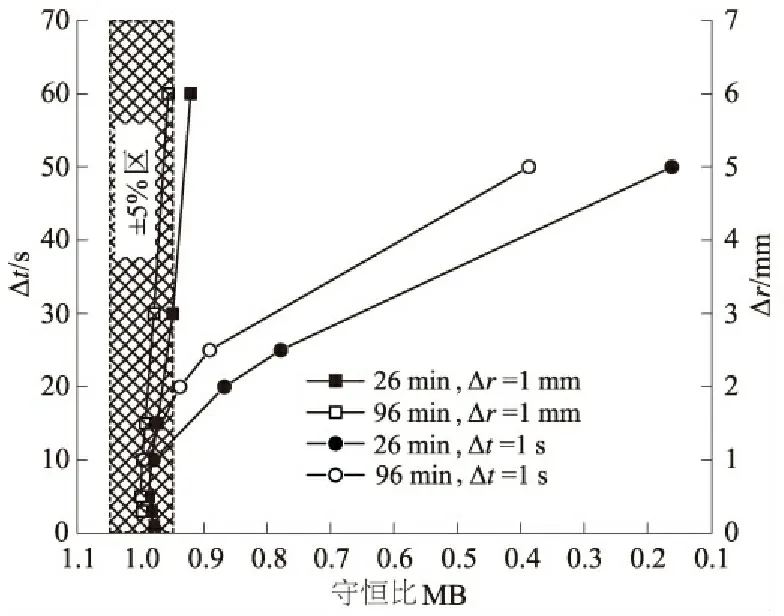
图7 以例1为例考察数值模型的物料守恒特性Fig.7 Test of materials conservation in the numerical model (example 1)

3.2 可行性争议与探讨

如前所述，Goforth[15]基于①非饱和状态下渗流速度的离心相似比可能不成立；②常规非饱和水流中，基质吸力梯度可能是重力势能梯度的10～1 000倍，认为将离心机应用于包气带水分迁移不太合适。Poulose等[16]通过实验观察认同Goforth[15]的结论，认为离心模拟只适合饱和水分及溶质迁移的研究。针对这一争议，本文按照以下步骤进行探讨：首先，认为“非饱和流的渗流速度、尺寸和时间的相似比分别为N，1/N，1/N2”是正确的；其次，为了判断离心模拟能否正确重现原型现象，利用Hydrus 1-D软件包直接对全尺度原型中非饱和水分迁移过程进行模拟预测；最后，将两者的模拟结果进行比较从而进一步分析判断。

此处的原型为一根均质装填低渗透性非饱和土土柱的水分入渗过程。土柱的初始含水率设为0.22 cm3/cm3，入渗水从顶部注入并保持通量恒定，土柱底部保持和水面接触，具体的输入参数见表3。

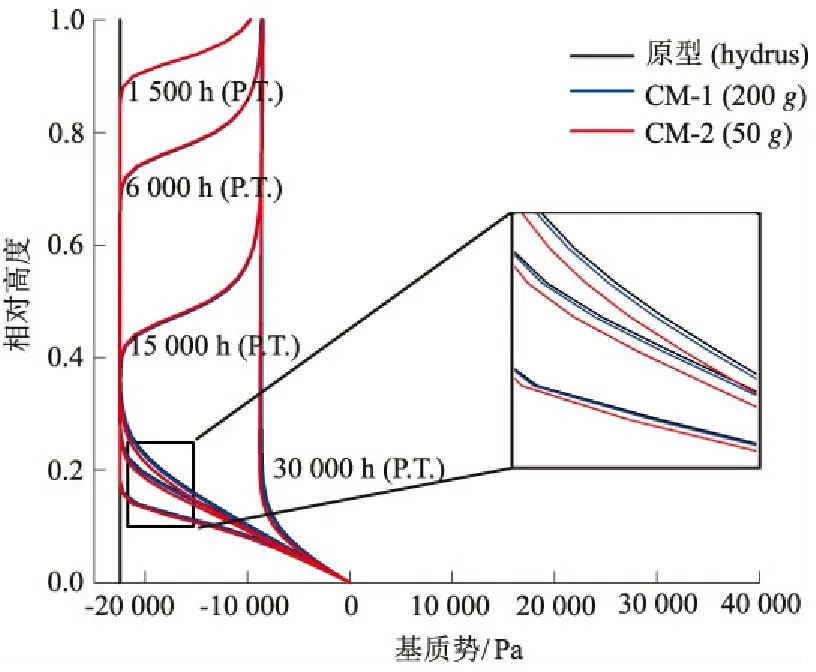
数值模型的模拟结果和Hydrus软件包直接模拟原型的结果对比如图8所示，可以看出两者几乎完全一致，表明离心模拟非饱和水流的相似比是正确的。细心观察图8，可看到在靠近底部时，模型和原型的数据匹配存在一定的偏差，离心模型的水分迁移要稍滞后于原型，这是由离心加速度的不均匀分布所导致的[3]。模型2/3高度处的相似比为N，而柱顶至2/3高度处离心加速度略小于Ng(相似比N)。另外，用同一离心设备模拟同一原型时，使用更高的离心加速度能够减轻这种现象。因为更大的N需要更小尺寸的离心模型，离心加速度分布更加均匀。

图8离心机用于非饱和水流可行性的数值检验
Fig.8Feasibilityofapplyingcentrifugeinunsaturatedwaterflowbynumericaltests

针对Goforth[15]给出的2个原因，本文从以下2方面进行探讨。

表3 数值模拟的输入参数Table 3 Input parameters of the numerical modeling

一方面，Goforth[15]忽略了能够满足渗流速率正比于重力水平的另一种情况，即基质吸力梯度(∂ψm/∂r)正比于重力水平。从图8可知，离心模型和原型对应位置处的基质吸力大小相等，离心模型的尺寸和原型相比缩小了1/N，所以离心模型中2点之间的基质吸力梯度大小应该是原型中对应2点间梯度的N倍，即基质吸力梯度和N成正比。故渗流速度的相似比为N是正确的，离心模拟技术可以正确反映原型中的非饱和水分迁移。

另一方面，离心模型和原型中位置势能梯度占总水势梯度的比分别为：

(22)

(23)

由于基质吸力梯度正比于重力水平N，所以ηm和ηp相等，这意味着离心不会强化位置势能梯度在非饱和带水分迁移过程中的重要性。

鉴于以上原因，本文认为Goforth[15]思考不严谨，其结论是不正确的。本文中的理论和数值模型都假设土的特性参数不随离心加速度的改变而改变，基于这一前提，可以说理论上离心模拟能用于包气带水分迁移的研究。但是在实际中存在许多因素能导致不确定性，如不理想的边界条件控制、压实现象的出现、安装的传感器性能、离心模型制作、加速度分布不均等，在进行包气带水分迁移离心模拟研究时，应该重视解决这些问题确保得到准确的结果。

3.3 理论分析与数值模拟的不足

本文针对离心模拟技术应用于包气带水分迁移研究的可行性而进行的理论分析和数值模拟依然存在其不足之处，主要表现为：①理论模型中忽略了水的动能，这对于一维离心模型非饱和水的势能的推导会产生影响，进而会对后续的数值模拟的结果产生影响，这种影响使得理论分析并没有完全描述包气带水分迁移的过程；②数值模拟过程中求解Richards方程要知道水力传导系数和基质吸力、含水率和基质吸力之间的关系，即渗透率函数K(θ)和土水特征曲线SWRC，而本文用于描述K(θ)和SWRC的模型是常用的Gardner模型和Mualem模型及Van Genuchten模型，此处并没有论证其它描述K(θ)和SWRC的模型是否可用于本文，这一点值得进行相关的探讨；③数值模拟部分验证了从文献中获取的4套数据，虽然这4套数据对应的4种情景足够对本文的议题进行探讨和验证，但在后续的进一步研究中，数值模拟部分可以将验证的情景进行扩展，以便更加深入地进行相关研究的探讨，本文作者在后续的研究中会对此进行考虑。