东营凹陷沙河街组页岩微观孔隙多重分形特征

王 民，焦晨雪，李传明，李 政，周能武，李进步，卢双舫，田福春，郝桂宪，石 瑾

（1.中国石油大学（华东）地球科学与技术学院，山东青岛266580；2.中国石化胜利油田分公司勘探开发研究院，山东东营257015；3.中国石油大港油田公司石油工程研究院，天津300280）

自1973年以来，济阳坳陷有800多口探井见到页岩油气显示，70多口井有页岩油气产出，其中35口井获得了工业油气流［1-3］，如济阳坳陷河54、罗42、新义深9和永54井，累积产油量均超过万吨，其中河54井累积产油量约为2.8×104t。页岩油是指以吸附态和游离态赋存于泥页岩及其薄夹层（岩性为粉砂岩、白云岩、灰岩或凝灰岩）中的液态石油，属于烃源岩内（源内）石油，不包括传统意义上的油页岩油，即固体矿产领域中通过热裂解、加氢催化或者热蒸馏技术使油页岩中有机质裂解从而得到的人造石油，也不包括经过短距离运移后在源外致密储层聚集的致密油［3-4］。页岩油富集在微-纳米尺度的孔裂隙中，不少学者开展了页岩储集空间的定性定量评价研究［5-14］，结果表明，页岩中发育的微小孔隙具有分形特征［14］，其分形维数与页岩油含量和黏土含量有一定关系［15］，LI建立了分形维数与岩石渗透率的关系［16］。然而单一的分形维数并不足以表征孔径分布特征，北美Bakken页岩及土壤科学中的相关研究结果表明，孔径及其分布具有多重分形特征［17-20］。

多重分形是一个由有限几种或大量具有不同分形行为的子集合叠加而成的非均匀分维分布的奇异集合，是原始分形概念对于非均匀分形的自然推广［21］。分形维数可以表征孔径分布的差异和自相似性，并反映其均匀程度［22］。为此，笔者通过对东营凹陷页岩油重点探井样品的低温氮气吸附实验分析，研究页岩微观孔隙是否具有多重分形特征，进而探讨分形维数与孔体积、渗透率、页岩矿物组成的关系，以及非均质性的控制因素，以期为明确东营凹陷沙河街组页岩的孔隙特征、非均质性和连通性提供依据。

1 区域地质概况

东营凹陷是济阳坳陷的次级凹陷，位于济阳坳陷的东南部，面积约为5 850 km2，由一系列基底断块组成，平面上呈现近NE向北断南超的复式半地堑特征，主要受NE和NEE向的张性、张扭性大断裂控制（图1）。在NS向上，一般可划分为缓坡、洼陷、陡坡等次级构造单元；在EW向上，一系列NW向或近NS向的断裂使构造复杂化［23］。古气候和古盐度影响着湖盆沉积体系的发育。在沙四段沉积时期，气候比较干旱，主要为滨浅湖沉积，以灰褐色钙质页岩、泥岩为主，夹薄层白云岩、泥质白云岩、碎屑白云岩、鲕状灰岩、油页岩和页岩，发育典型的层间层理，富含生物化石；在沙三段下亚段沉积时期，气候变暖，湖水含盐度下降，转化为半咸水湖泊，为深湖沉积，以暗色纹层状泥页岩和层状页岩为主；此后，湖水继续淡化，至沙三段中亚段沉积时期转化为淡水湖泊；在沙三段上亚段沉积时期，气候开始向干旱转化，属微咸水湖泊；沙二段至沙一段沉积时期为半干旱半湿润的气候条件，又转化为半咸水湖泊。

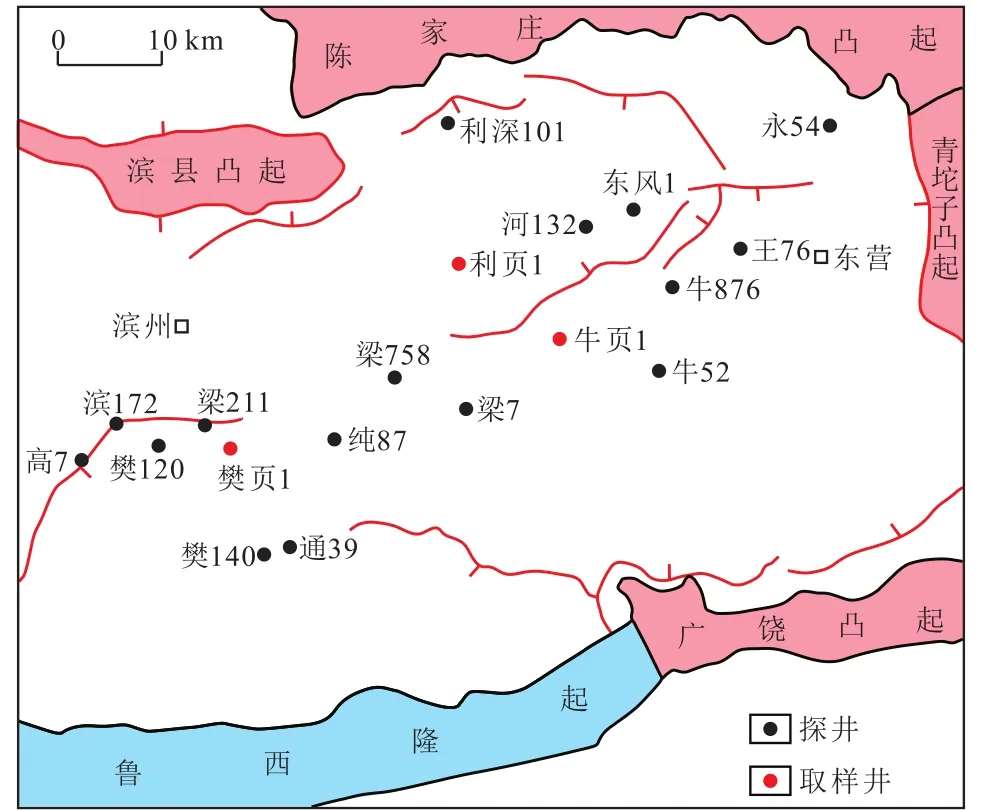
图1 济阳坳陷东营凹陷区域构造位置及取样井分布Fig.1 Simplified structure map and distribution of sampling wells of Dongying Sag，Jiyang Depression

2 实验岩样与方法

实验所用的57块页岩样品取自东营凹陷页岩油重点探井（樊页1、利页1、牛页1）的沙四段、沙三段，埋深为3 030～3 833 m，总有机碳含量为0.78%～6.58%。

岩石热解分析采用Rock-Eval6型热解仪，按照GB/T 18602—2012［24］进行分析；总有机碳含量采用CS-600型有机碳分析仪，按照GB/T 19145—2003［25］进行分析；岩石矿物组成采用RigakuMiniflexII仪，按照SY/T 5163—2010［26］进行分析。

采用美国麦克ASAP2460孔径分析仪，将页岩样品分为2份，其中一份进行洗油，另一份不洗油。洗油有机溶剂为二氯甲烷和丙酮，两者体积比为3∶1，洗油时间为7 d。2份样品分别开展低温氮气吸附实验。共设置35个相对压力点，其值为0.010～0.995，吸附平衡时间为10 s。具体实验步骤包括：①称取10 g目数为80～100的页岩样品，装入与吸附仪相连的样品管中，加热至110℃，去除样品内部的水和易挥发性杂质，进一步将样品和仪器抽真空去除其他气体成分；②使用相应实验吸附质（氮气）对样品进行回填，在恒定温度下，逐步升高和降低气体分压，并测定页岩在相应条件下的吸附和脱附量；③通过多点BET方程和BJH方程分别计算得到页岩的比表面积和孔径分布。该实验在中国石油大学（华东）非常规油气研究中心完成。

3 多重分形模型

采用计盒法研究低温氮气吸附数据（反映孔径分布的非均质性）的多重分形特征。在分析区间[A,B]内低温氮气吸附体积概率时，需要确定标度和测度。标度和测度表达式分别为：

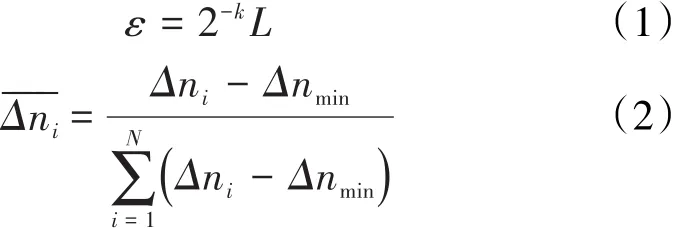
本次研究中相对压力变化区间为0.010～0.995，共划分为34段（35个吸附测点数据）。

在标度变化的情况下，区间[ ]A,B内氮气吸附体积概率须满足：

ai可反映局部的奇异强度，其值较高代表数据的平滑或规则性或整齐性越高，相反，其值较小代表数据变化程度越大或不规则性越强。ai与所在的区域有关，反映所在的区域概率的大小。

得到奇异性指数后，将研究对象划分为一系列子集，使得每一个子集内的小单元都具有相同的奇异性指数，然后计算这个子集内的单元个数，定义单元个数与标度的关系式为：

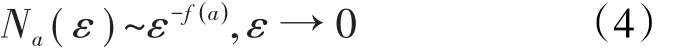
f(a)为多重分型谱，是具有相同奇异性指数的子集的分形维数。一个复杂的分形体，其内部可以分为一系列不同奇异性指数表示的子集，f(a)则给出了这一系列子集的分形特征，如果研究对象是单分形的，则f(a)为一定值；如果是多重分形的，则f(a)一般呈现单峰图像。

奇异性指数（a）与f(a)可以通过CHHABRA和JENSEN法［27］进行求解，其表达式分别为：

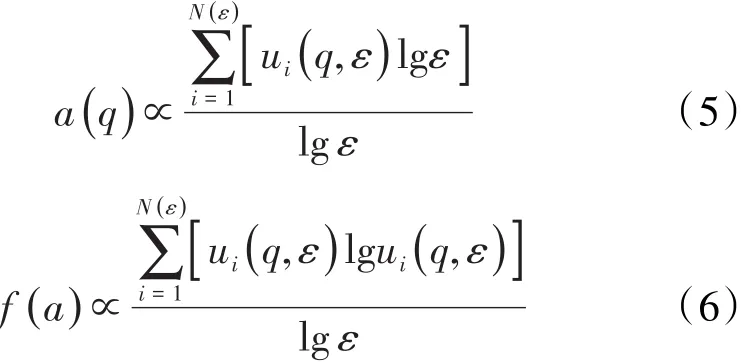
其中

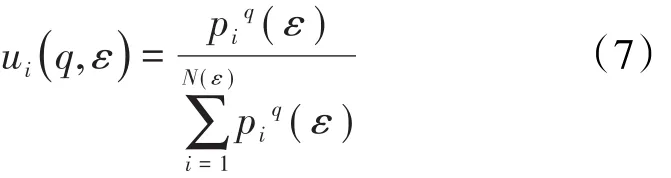
当q≫1时，大浓度或高聚集度（稠密区）的信息被放大；当q≪1时，小浓度或低聚集度（稀疏区）的信息被放大，本次研究q从-5到5变化，步长为0.25。a和f(a)通过（5）式和（6）式线性回归得到。对于多重分形，（7）式中的分母为配分函数，也称为统计矩函数，其表达式为：

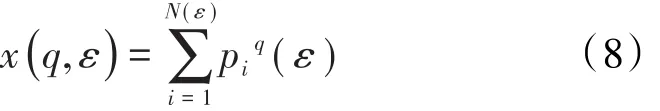
定义x(q , ε)的目的是展示函数pi(ε)的大小。从（8）式可以看出，假设pm(ε)≫ pj(ε)，当q≫ 1时，在(ε)中，显然是 pm(ε)起主要作用，此时x(q,ε)反映的是概率较高（或稠密）区域的性质。所以在q→∞的条件下，可只考虑pi(ε)的最大值而忽略其他小概率值，这就简化了x(q,ε)的计算。反之，当q≪1时，这时x(q,ε)反映的是概率较小（或稀疏）区域的性质。这样通过加权处理，即可将一个复杂的过程划分为具有不同奇异程度的区域来研究。

对于一给定的统计矩阶q，称满足x(q,ε) ∝ ετ(q)的函数τ(q)为质量指数函数，它是分形行为的特征函数。若τ(q)与q呈直线关系，则研究对象是单分形的；若τ(q)与q呈凸函数关系，则研究对象具有多重分形特征。

a～f(a)是描述多重分形局部特征的一套基本语言，另一套为q～D(q)，是从信息论角度引入。D(q)的计算式为：

当q=1时，D(q)的计算式变为：

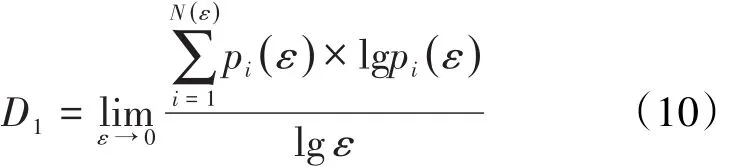
广义分形维数与多重分形谱之间满足Legendre变化，其表达式为：

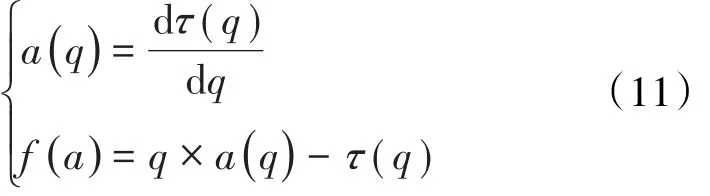
（11）式构建了独立变量q和τ及独立变量a和f之间的联系，均可以用来描述多重分形特征。

4 结果与分析

4.1 页岩孔隙多重分形的客观性

如果一个研究对象存在多重分形特征，则需满足3个条件：①D(q)和a(q)与q呈严格单调递减；②τ(q)与q呈严格递增的凸函数；③f(a)与a呈凸函数关系。由页岩样品低温氮气吸附数据的多重分形计算结果可以看出，x(q,ε)与lgε呈很好的线性关系（图2a），表明由低温氮气吸附数据得到的孔径分布表现为多重分形特征。当q＞0时，x(q,ε) 与 lgε呈负相关，当q＜0时，x(q,ε) 与 lgε呈正相关，也就是说在统计矩阶从小到大的变化过程中，质量指数函数（即拟合方程的斜率）从负数逐渐向正数变化，且x(q,ε)与lgε的拟合线由稀疏逐渐变得密集，反映出页岩孔隙孔径分布比较集中，主要分布在孔隙较小的区间。

由图2b可见，τ(q)随q的增加严格递增，呈现出上凸的特征。D(q)的形态及随q的增加严格单调递减（图2c），表现出反S型。对于均匀分形，D(q)与q的关系曲线是一条直线，对于非均匀分形，两者表现出一定过渡的递减函数，D(q)与q的关系曲线越陡，D(q)的值域越大，即不同奇异强度分形结构分布范围越大，分形结构的非均匀性就越大。f(a)与a呈现凸函数特征（图2d）。图2中的现象与判断多重分形存在与否的特征相符，说明页岩微观孔隙多重分形是客观存在的。洗油后样品的f(a)的最大值与最小值差变大，表明洗油后样品中孔径分布的差异更加明显，也暗示出不同级别孔隙中的页岩油含量的不同。

4.2 多重分形参数之间的关系

除多重分形谱的右半偏参数（a-5-a0）和左右半偏参数之差（Rd）与其他分形参数相关性较差外，多重分形参数之间表现出很强的相关性（表1）。信息维数（D1）、关联维数（D2）和Hurst指数呈现正相关关系，与其他参数均为负相关关系。Hausdorff维数（a0）和左半偏参数除与信息维数、关联维数和Hurst指数呈负相关外，与其他参数均为正相关关系。多重分形谱峰宽与广义多重分形参数（信息维数和关联维数）呈负相关关系，与孔隙分布的非均质性呈正相关。信息维数与Hausdorff维数表现为负相关关系，Hausdorff维数越大，信息维数越小，孔径分布越不平缓或越集中（图3a），与前文结论一致。从图3b可以看出，峰宽（a-5-a5）与孔隙分布的非均质性（D-5-D5）两者呈现出非常好的正相关关系，孔隙分布的非均质性越强，（D-5-D5）越大，峰宽（a-5-a5）值越大，非均质性强，内部差异大。

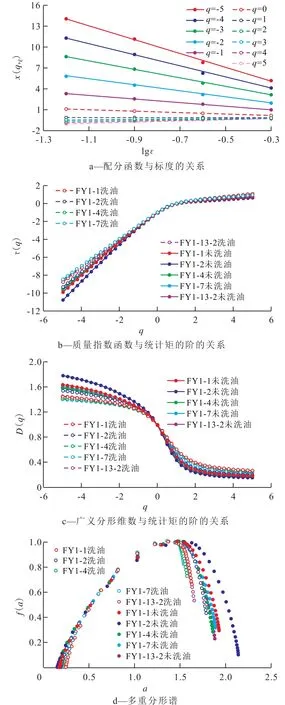
图2 樊页1井岩样低温氮气吸附数据多重分形特征Fig.2 Multi-fractal characteristics of Well Fanye1 core sample measured with low temperature N2adsorption

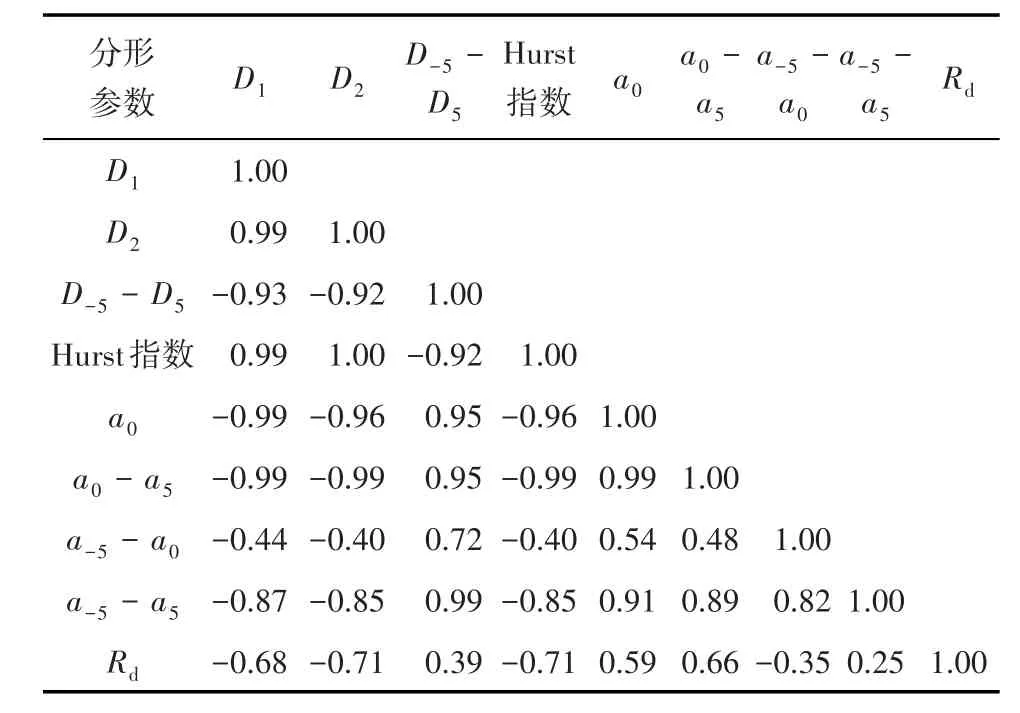
表1 济阳坳陷东营凹陷沙河街组页岩多重分形参数相关关系Table1 Correlations among the multi-fractal parameters of Shahejie Formation shale，Dongying Sag，Jiyang Depression

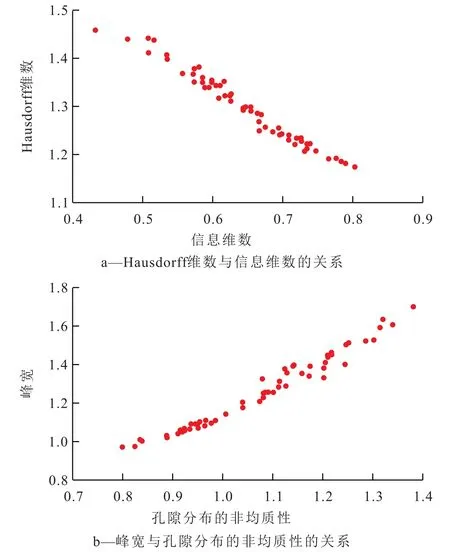
图3 基于低温氮气吸附数据计算的页岩孔隙多重分形参数之间的关系Fig.3 Relations among the multi-fractal parameters derived from low temperature N2adsorption data

奇异谱的形态和局部特征提供了吸附数据内部结构的大量信息。多重分形谱的峰宽越宽，局部非均质性越强，右半偏大反映了奇异性指数更具多样性，与测定物概率分布较低有关（孔径分布稀疏区）。相反，左半偏大意味着具有最小奇异性指数的多样性，与较高聚集概率有关（孔径分布稠密区）。研究样品的Rd值均为正值，表明孔径分布主要受控制于孔径分布稠密区。

4.3 多重分形参数与孔隙参数的关系

Hausdorff维数反映了孔径分布局部密集程度，其值越小，分形谱越往左偏（图4a），孔隙孔径分布局部越密集（图4b）。Δf（f(a)最大值与最小值之差）的绝对值越小，多重分形谱的不对称程度越小（如FY1-31岩样），表明疏密程度对孔径分布影响较小，FY1-31，FY1-18，FY1-27，FY1-21，FY1-32和FY1-16岩样的Δf绝对值依次逐渐增加，局部疏密区域在孔径分布上差异也越明显（图4b）。

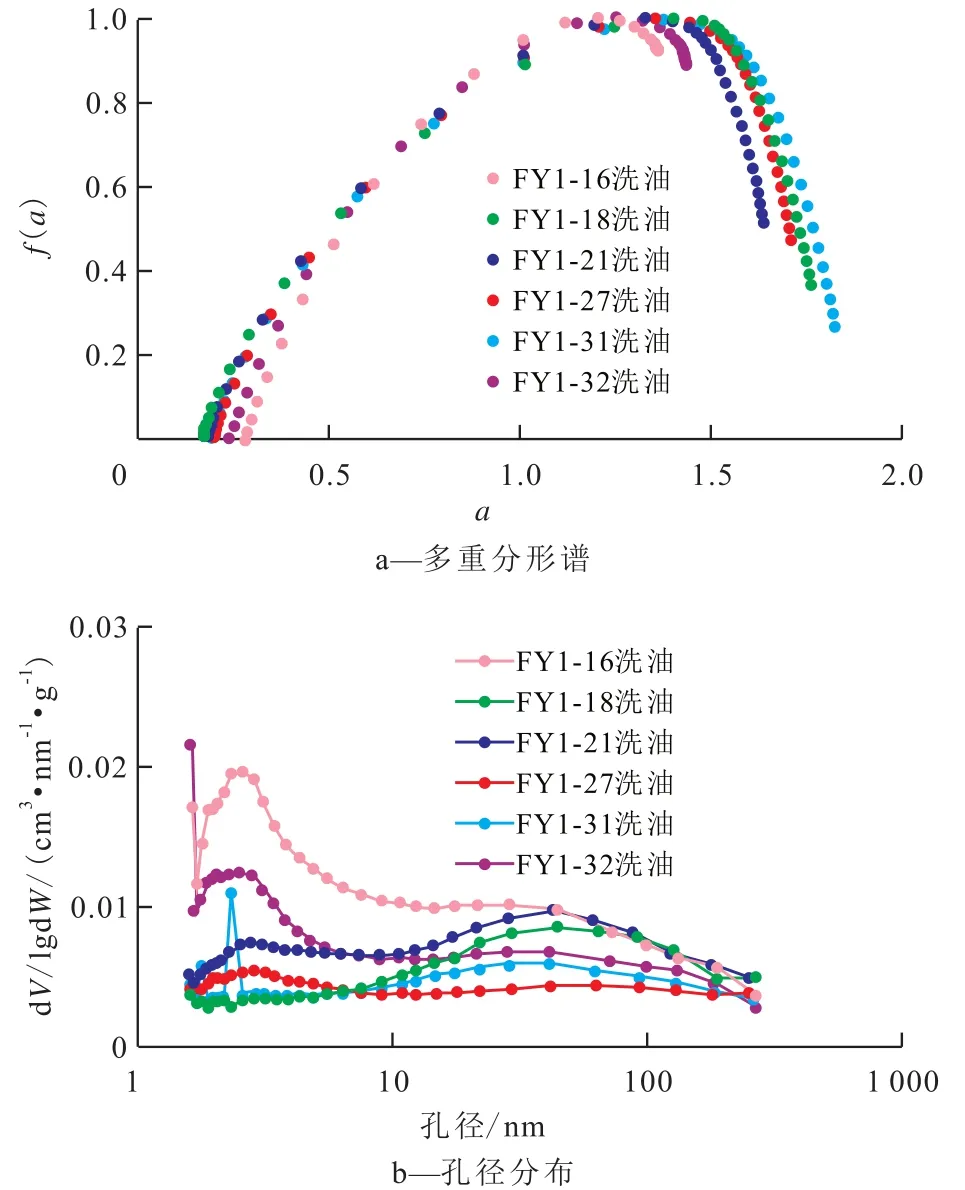
图4 基于樊页1井岩样低温氮气吸附数据计算的多重分形谱及孔径分布Fig.4 Multi-fractal spectrum and pore size distributions of Well Fanye1 core sample calculated by low temperature N2adsorption

从多重分形参数与页岩孔隙比表面积和孔体积的关系可以看出：Hausdorff维数与比表面积呈较好的负相关关系，Hausdorff维数越大，比表面积越小（图5a），反映出孔体积较小；Hausdorff维数与孔体积表现出弱负相关关系（图5b）；峰宽与比表面积也呈现负相关关系，随着峰宽的增加，比表面积逐渐降低（图5c）。

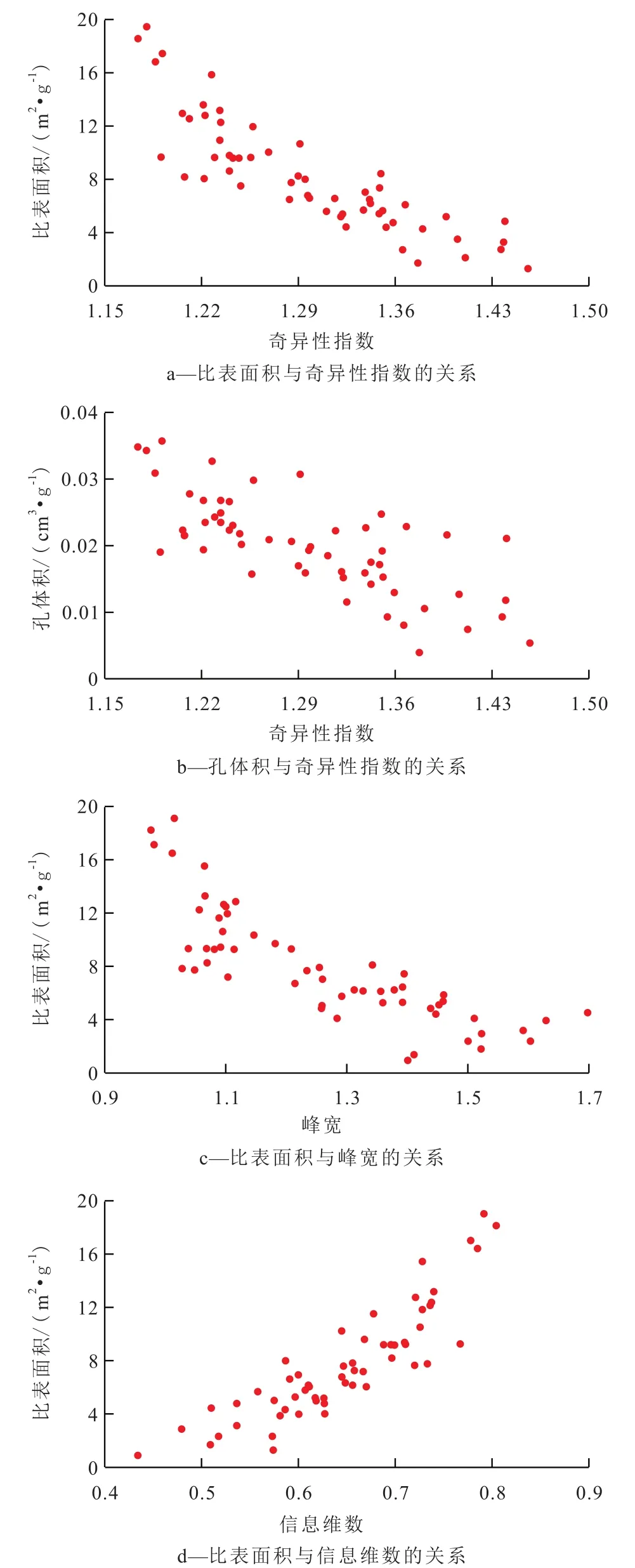
图5 东营凹陷沙河街组页岩孔隙多重分形参数与孔隙参数的关系Fig.5 Relations between multi-fractal parameters and pore parameters of Shahejie Formation shale，Dongying Sag

Hurst指数可用来反映孔隙的连通性，一般为0.5～1，Hurst数值越小，孔隙连通性越差，数值越大说明孔隙连通性越好。东营凹陷沙河街组页岩的Hurst指数为0.61～0.82，说明该区页岩样品内部孔隙的连通性一般。由Hurst指数与页岩渗透率的关系（图6）可以看出，渗透率随着Hurst指数的增大而增大。

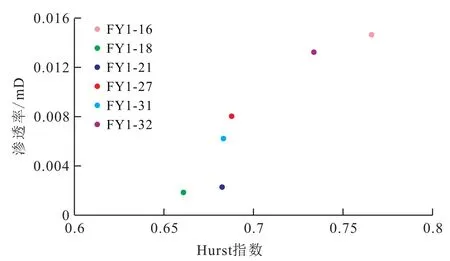
图6 东营凹陷沙河街组页岩Hurst指数与渗透率之间的关系Fig.6 Relationship between Hurst index and permeability of shale，Shahejie Formation，Dongying Sag

广义维数谱中常用的参数有容量维数、信息维数和关联维数，当三者相等时，得到的孔径分布具有单分形特征，信息维数反映低温氮气吸附数据疏密程度的多样性，即对应孔径分布的集中程度，其值越大，孔径分布越平缓，其值越小，孔径分布越集中；关联维数主要反映孔径测量间隔的均匀性，较低的关联维数意味着较小的孔径关联度。本次研究所有样品的容量维数均为1，与土壤科学领域其他学者得到的结果相似，表明所划分区间内均有氮气吸附，信息维数与比表面积呈现很好的正相关关系，随着信息维数的增加，比表面积增加（图5d）。

4.4 多重分形参数与页岩组成及相关参数之间的关系

由济阳坳陷东营凹陷沙河街组页岩多重分形参数与页岩组成及相关参数的相关关系（表2）可以看出，信息维数、关联维数和Hurst指数等多重分形参数与比表面积、孔体积呈正相关关系，除右半偏参数外，其他多重分形参数与比表面积、孔体积呈负相关关系，其中与比表面积的相关系数高于与孔体积的相关系数，与图5一致。岩石热解参数及页岩矿物含量与多重分形参数没有明显的相关性，仅与裂解烃热解峰温呈现出弱相关关系。

由于采用低温氮气吸附数据获得的多重分形参数反映的是孔径分布的非均质性，故表2表明，孔径分布的非均质性主要受比表面积和孔体积的影响，与页岩其他组成无关。高过成熟页岩孔隙发育的主控因素为有机质丰度，因此有机质丰度和成熟度将会是高过成熟页岩孔隙孔径分布非均质性的影响因素，但对低熟-成熟阶段的湖相页岩而言，孔隙发育程度与有机质丰度没有较好的相关性，孔隙发育的控制因素更加复杂。多重分形的方法提供了一个很好的描述岩石孔隙内部结构的方法。

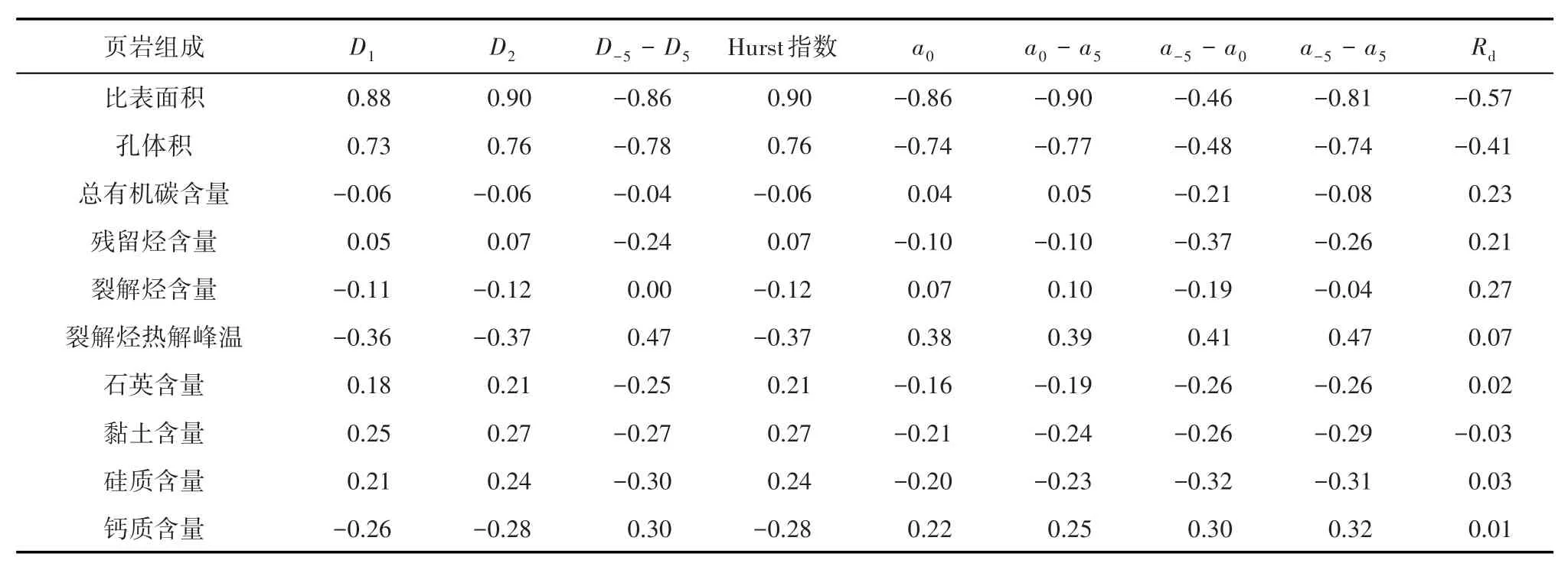
表2 济阳坳陷东营凹陷沙河街组页岩多重分形参数与页岩组成及相关参数之间相关关系Table2 Correlations between multi-fractal parameters and shale composition and other parameters of Shahejie Formation，Dongying Sag，Jiyang Depression

5 结论

通过对济阳坳陷东营凹陷沙河街组湖相页岩低温氮气吸附数据的多重分形研究，发现页岩的孔隙存在明显的多重分形特征，可以用多重分形谱或广义分形维数揭示孔径分布的非均质性。沙河街组页岩孔径分布的非均质性受控于孔隙的比表面积，与页岩有机组成及矿物含量等没有明显关系，多重分形参数之间存在明显的相关关系，Hurst指数与渗透率呈现正相关关系。

符号解释：

A，B——低温氮气吸附数据下限和上限；ε——标度；k——划分区间的段数，k=0，1，2，…；L——低温氮气测定过程中p/p0的区间；p——压力，Pa；p0——饱和蒸汽压，Pa；Δni——连续2个氮气吸附数据的变化值；i——实验测点序号；N——实验测点总数；pi——第i个区间内氮气吸附体积概率值；ai——集合中的第i个奇异性指数；Na(ε)——单元个数；a——奇异性指数集合；f(a)——具有相同奇异性指数的子集的分形维数；q——统计矩阶；x(q ,ε)——配分函数，也称为统计矩函数；τ(q)——质量指数函数；D(q)——广义分形维数谱；D1——信息维数；V——孔体积，cm3；W——孔隙宽度，nm；Rd——左半偏与右半偏差值；D2——关联维数；D-5-D5——孔隙分布的非均质性；a0――Hausdorff维数，统计矩阶等于0时的奇异性指数；a0-a5——左半偏参数；a-5-a0——右半偏参数；a-5-a5——峰宽。