基于协方差理论的非关联轨道动态关联算法
2019-01-21,,,
,,,
1. 中国科学院 国家空间科学中心,北京 100190 2. 中国科学院大学,北京 100190
在国内外编目实践中,一些突发的情况会对正常的编目工作产生不利的影响,例如太阳爆发干扰了大气,使得空间目标的预报精度大大降低,也降低了对近地目标的编目维持能力,由于极端空间环境条件下大气模型精度有限,影响了大量的轨道预报精度,使得目标丢失。一些突发的卫星事件解体会在很短时间内增加数以千计的可跟踪目标[1-3]。在这种情况下,设备监测到的许多目标可能没有编目,非关联轨道 (Uncorrelated Tracks,UCTs)数据和没有编号的目标大大增加,目标编目数据处理中心的负担立即增大。此外在目标解体初期,目标的空间密度还可能引起目标混淆。这两种情况必须在处理中心增大处理能力,以及增加额外的关联过程来克服。大型卫星星座的部署也会增加许多空间目标。有些空间碎片可能已处于设备探测能力的边缘,在观测条件较好时,设备偶然能得到观测数据,但是,观测数据不足以维持该目标的编目,因此目标可能丢失。对于光学观测设备,还有可见期的问题[4-10]。
解决这些问题除了增加探测网的探测能力及提高轨道预报精度外,还需要改进关联算法。采用基于协方差理论关联算法可以提高短弧段雷达观测数据和稀疏可见期数据的关联水平。该计算方法旨在解决UCTs自动关联问题,建立一个更完整的空间对象编目库。基于协方差的轨道关联动态算法是基于轨道不确定性协方差的动态算法,利用轨道数据的协方差信息生成完整的轨道状态和误差分布函数,并用于统计关联轨道。如果协方差准确表示实际轨道误差分布,那么这个算法是最优的、最大化的概率关联。协方差矩阵可以更有效统计和自动方式关联UCTs。基于协方差的关联已经在精密轨道摄动的模拟中测试,可完成编目10万个空间目标[11]。仿真结果表明,相对于之前固定门限方法的轨道关联,基于协方差的轨道关联可降低错误关联值达两个数量级。基于协方差的数据关联方法将提高空间监测网低轨道雷达监测数据的编目分辨能力。
本文建立了线性和无迹卡尔曼滤波协方差生成和演化算法,分析了两种协方差演化的精度,无迹卡尔曼滤波的协方差演化方法相对线性协方差演化方法有较高的演化精度。把协方差演化方法应用到印度一箭104星中的20颗卫星轨道关联中,仿真结果表明采用基于协方差轨道关联具有很好的关联效果。
1 基于轨道协方差UCTs动态关联算法模拟分析方法
基于协方差的UCTs动态关联算法是把轨道协方差作为关联时的影响因素,关联量是复合等概率椭球。当探测器的测量误差是高斯分布并且轨道动力学为线性时,协方差关联是最佳关联量。采用此关联方法,相同坐标系下两卫星的状态量和协方差须预报到同一时刻。例如,可以从先前t1时刻的轨道和协方差预报到t2时刻轨道,两轨道状态差为:
X2,1=X2(t2)-X1(t2)
(1)
式中:X1(t2)和X2(t2)为空间目标在t2时刻的轨道状态,包括位置和速度。关联过程中通过计算统计量k来衡量两卫星的关联程度。k属于χ2统计,也被称为马氏距离:
k2=[X2,1]T[P1(t2)+P2(t2)]-1[X2,1]
(2)
式中:P1和P2分别为两卫星的轨道协方差矩阵。
为了实际模拟基于协方差的轨道关联,需要模拟空间目标监测网的监测模型和编目过程。决定从真实雷达测站出发,不同雷达测量数据随机加入测量噪声,模拟雷达测距及测角数据。定轨模块对这些测量数据进行初始轨道确定及最小二乘处理生成轨道及协方差数据。关联模块根据定轨目标的协方差数据进行演化实现与编目库和非关联目标的关联。
1.1 真实轨道
真实轨道是由数值轨道传播器生成的。动力学方程模型包括太阳辐射光压,空气阻力密度模型,第三体的影响作用力和21×21阶的重力场[12]。50个物体的轨道状态取自轨道碎片编目。这些物体是从空间目标目录里半长轴为6860~6890之间抽样的。目标的横截面积设为常值,面积和质量与碎片编目的值相同。设置每一个物体的阻力系数和光压反射系数为默认值。空间目标轨道摄动动力学模型采用的是EGM2008的21阶地球重力场模型,NRLMSISE2000大气阻力模型,球形光压模型。依据轨道摄动方程演化计算理论上空间目标的真实轨道[13]。
1.2 雷达探测器模拟
依据现有的雷达跟踪测量站,模拟空间目标的跟踪测量数据。用国外公布的雷达参数对雷达跟踪站进行建模。表1所示这些参数来自美国巴利亚多(Vallado)[14]。对雷达的观测数据进行模拟,包括测距范围、仰角、方位角、雷达高度、测距标准差、仰角标准差以及方位角标准差。在观测数据中加入了高斯噪声[15]。每一步都用标准差生成随机偏差模拟高斯噪声。采用这种标准差是因为根据一段时间对雷达探测器的分析显示日常偏差标准差与测量标准差大致相等。如果观测数据超出了方位角和仰角的限制就要去掉[16]。假定某个空间目标截面积为1 m2时观测站最大测量距离为ρmax。雷达的返回值与1/ρ4成正比,其中ρ是测距,所以观测量应满足:
(3)
式中:A为空间目标截面积,两次测量之间为10 s间隔时,观测数据设置限制在2′弧段内。每个雷达探测器被分配最大数量的可跟踪目标。
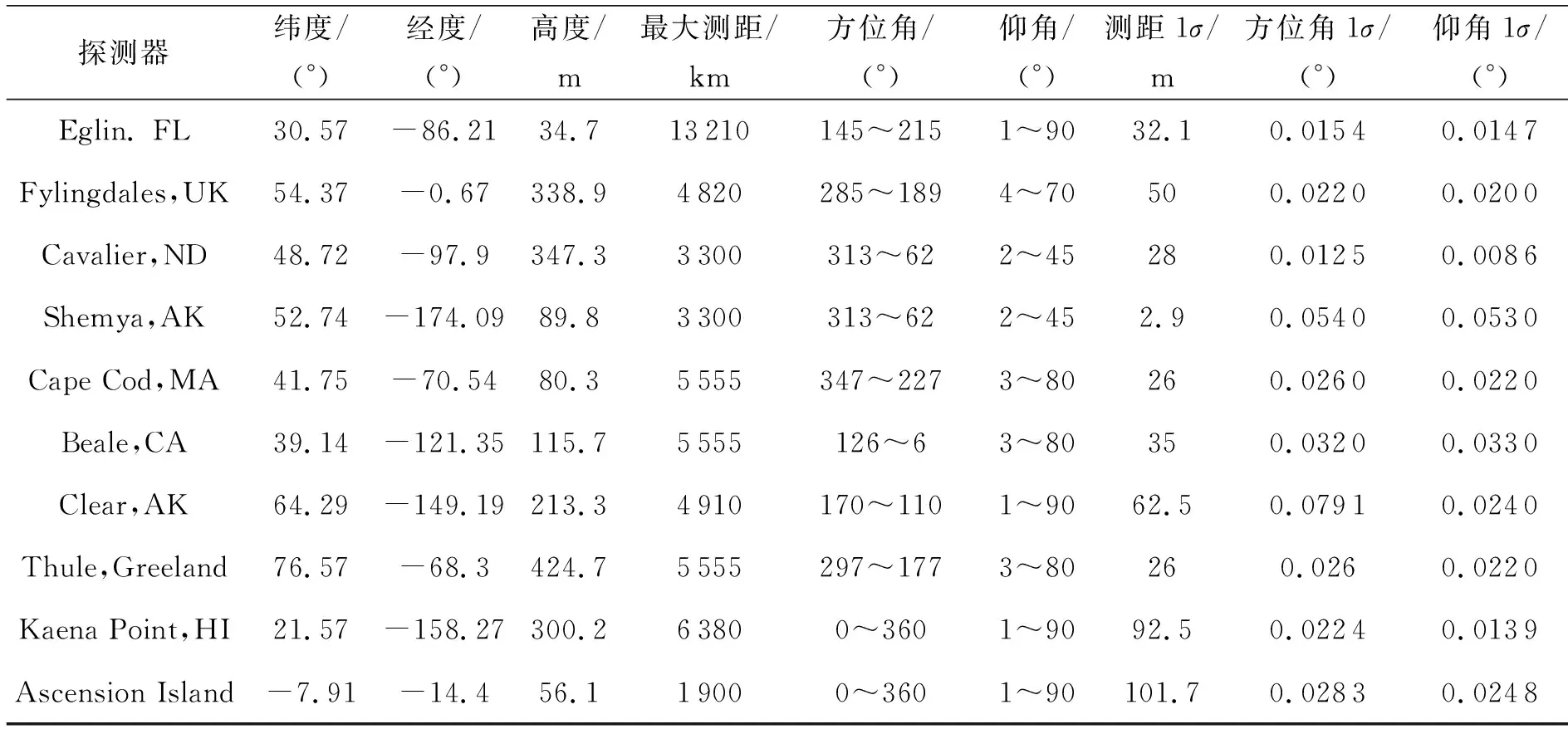
表1 雷达探测器参数
1.3 轨道确定协方差
为了测试k值是否可以用来关联编目轨道,选取物体的一个子集部分构成了模拟目录。选用目录里每个物体的第一轨道,使用测距、方位角、仰角三要素方法进行初始轨道确定。轨道状态估计作为最小二乘批处理程序的先验状态。当执行最小二乘批差分校正时,每一个目录物体所有前三天的观测数据合并在一起。每个物体的面积和质量都设为默认值(1m2和100 kg),但是要估计阻力系数及光压反射参数的修正值[17-18]。在轨道计算中用数值计算轨道的传播。在未来大于三天的时间里,物体估计状态随时间传播且储存为星历表、用来做为一条空间物体目录。50个空间物体只有30个创建了编目星历,其他物体的星历未知。
在先验目录创建后,所有的真实轨道在未来24 h传播。用真实轨道可以形成观测数据,且已知物体的每个轨道都被设置了编号。最小二乘差分校正用来获得每个轨道的状态和协方差估计。由于这些轨道相当的短(120 s),这些单个轨道的估计有很大的不确定性,这在协方差上得到了反映。
1.4 数值积分模型的轨道协方差演化
1.4.1 误差演化线性化方法
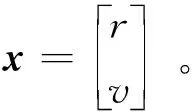
(4)
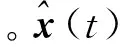
(5)
对式(5)微分:
(6)
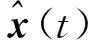
(7)
e(t)=Φ(t,ti)ei+wd(t,ti)
(8)
其中,状态转换矩阵Φ(t,ti)满足:
(9)
线性协方差转换矩阵Φ(t,ti)计算过程中忽略了高阶项的影响,只考虑了一阶项。线性协方差演化是一种分析方法,其优点是计算简化高效。但是对于非线性程度高、协方差演化周期长或初始协方差较大情况其计算精度较低[19],不适用于非高斯协方差演化。
1.4.2 UKF协方差演化方法
UKF是基于确定性样点计算的滤波算法,以Unscented变换为基础,采用卡尔曼线性滤波框架和确定性采样方式进行滤波。UKF采用一组有效的采样点来将状态近似为高斯随机变量,捕捉高斯随机变量的均值和协方差。当状态量通过实际的非线性系统之后,后验均值和协方差可以精确到三阶(泰勒展开)。由于不需要推导和计算Jacobian矩阵,基于UT的UKF算法更便于实现。

(1)构造Sigma点
(10)
(2)利用Sigma点进行非线性传播
根据计算所得Sigma点直接按照离散化非线性模型进行状态和观测预测,对应产生的Sigma样本点为:
χk(i)=f[χk-1(i),k]
(11)
式中:χk(i)(i=0,…,2n)为预测的对称分布Sigma点。
(3)根据样本点计算状态均值和方差
(12)
(13)
从上面的3个步骤中可以看出,Unscented变换不需要计算非线性函数的雅可比矩阵,变换中仅涉及函数计算,即使系统的模型比较复杂的情况下,算法实现的难度也并不会增加。
1.5 UCTs关联
处理这些轨道的第一步是比较星历看轨道是否属于已经存在的编目物体,然后更新编目星历。对于与已经编目在案的轨道相符的轨道,采用轨道状态值和协方差计算关联量k值。如果k值小于限定阈值,则认为该轨道匹配且轨道的标识或者标签保持不变。如果k值大于限定阈值,则更改标签以表明它是不相关轨道即UCTs。然后就是把UCTs与所有编目里的物体进行比较。为了减少比较数量,采用预测滤波的方法只选择轨道根数大致相当的星历。如果比较值k小于限定阈值,则该轨道被标记为属于物体编目。接着,所有被分配到编目里的新轨道与先前确定的轨道结合形成新的星历。这些综合的观测数据用来估计一个更新的编目轨道并创立一个新的、为期三天的预报编目星历。下一步就是UCTs与UCTs之间的关联,所有的UCTs形成一个候选轨道数据库,不能与编目库关联的轨道再与UCTs候选轨道关联。
2 模拟分析
2.1 协方差演化分析
低轨道目标分别选取400 km轨道高度的近圆轨道目标国际空间站和1 500 km轨道高度的近圆轨道目标Ajisai卫星。对国际空间站和Ajisai卫星设定初值协方差,采用线性协方差演化方法和UKF协方差演化方法计算演化时间为一天时,空间站和卫星的轨道协方差在RSW坐标系下的分量。RSW坐标系的R轴(径向)是从地球指向航天器方向的矢量,S轴(横向)在轨道平面内垂直于R轴,W轴(垂迹)垂直于轨道面。把演化结果同STK软件中高精度轨道(HPOP)协方差演化结果比较,分析两种方法协方差演化精度。轨道摄动力主要考虑地球引力、大气阻力、光压摄动力及第三体引力。地球引力采用的是21阶的EGM2008模型,大气阻力采用的是NRLMSISE2000模型,大气阻力系数Cd=2,光压系数Cr=1.8。
假设在J2000坐标系下空间站位置三方向初值误差均为10 m,速度三方向误差均为0.01 m/s。空间站协方差演化时长为一天,选取演化时长中的100个点,比较线性方法和UKF方法演化的100个点与HPOP协方差演化的误差。图1中前3个图采用是两种方法与HPOP对R、S、W三个方向的演化误差进行比较,最后1个图是采用STK中的HPOP对空间站轨道协方差的演化结果。
相比较发现,线性方法在S方向一天的协方差演化误差是米量级,UKF方法演化误差是分米量级。UKF协方差演化误差精度高于线性方法1个量级。
采用同样方法对Ajisai卫星轨道协方差演化,结果如图2所示,相同的初值协方差Ajisai卫星通过HPOP方法协方差演化一天的值小于空间站的演化值。这主要是空间站所受的大气阻力大于Ajisai卫星。对于Ajisai卫星S方向演化一天的误差,线性方法是米量级,UKF方法演化误差是厘米量级。UKF误差精度高于线性方法两个量级。对于低轨道空间目标,轨道高度越高,UKF协方差演化误差精度越高。
从图1和图2可以看出,对于空间站和Ajisai卫星,通过UKF方法演化的R方向协方差误差大于线性方法演化误差。这是由于轨道协方差随时间演化呈现非高斯性引起的。采用蒙特卡洛方法可以验证当轨道协方差演化时长为一天时,空间目标的轨道协方差不再是高斯分布的椭球,而是呈月牙状。月牙的弯曲方向就是在径向(R方向)。图3是采用蒙特卡洛方法演化的轨道协方差分布图。对Ajisai卫星初始根数加上位置标准差10 m、速度标准差0.01 m的随机误差,构成10 000个采样点,含随机误差的采样点在与HPOP相同模型摄动力作用下向前传播一天,把演化后的10 000个采样点与标准精密轨道相差得到蒙特卡洛误差采样点分布。从图3可以看出蒙特卡洛采样点分布不再是标准椭球形,采样点分布在R方向呈现弯曲的非高斯性分布。这种非高斯性弯曲分布导致R方向误差协方差值变大,而UKF方法可以比较明显地表示这种协方差演化特性。
2.2 UCTs关联模拟
选取2017年2月印度发射的一箭104星中的20个目标卫星做UCTs关联,卫星轨道半长轴6 860~6 890 km,轨道倾角97.5°,卫星轨道区域分布比较集中。各颗卫星之间具有相似的轨道类型,在与箭体分离后一段时间各个卫星在同一轨道面上,轨道之间只存在较小的相位差异,采用之前半长轴、轨道倾角筛选再进行空间目标编目存在困难,适用于验证基于协方差算法轨道关联。
每颗卫星选取2~4个不同时间点的轨道星历,轨道间隔小于两天。采用美国巴利亚多(Vallado)提供的雷达参数模拟20个目标卫星的雷达观测数据。并用HerrickGibbs方法对短弧段各个卫星初始轨道进行定轨,用最小二乘法对轨道进行精密定轨,生成卫星在某点的轨道根数及协方差信息。应用轨道预报方法对轨道根数进行数值预报,通过线性协方差演化方法和UKF协方差演化方法对卫星初始协方差进行演化。
20个UCTs模拟真实轨道是基于space-track提供的两行轨道根数,由于公布的两行轨道根数不包含轨道协方差信息,因此假设其为真实轨道重新定轨生成协方差。而两行轨道根数本身含有轨道误差,这可能是关联过程中关联阈值较大的主要原因。同时两行轨道根数是以真赤道平春分点(True Equator Mean Equinox,TEME)作为参考坐标系,需要转变为J2000坐标系分析。
图4是20个卫星中,相同卫星不同历元轨道根数进行协方差关联的关联量k值的统计分布情况。可以看出20颗卫星UCTs关联量分布主要在60~80。分析发现当UCTs关联阈值限定为200时,20颗卫星中相同卫星不同历元的轨道根数都可以成功关联。关联值大的原因作者分析如下:
1)首先文章中选用美国发布的两行轨道根数,这种根数本身存在较大的轨道误差。由于模拟中选取20颗卫星的两行轨道根数作为真实轨道,忽略了两行轨道根数数据本身所含有的误差,所以计算的关联阈值较大。
2)在雷达观测数据模拟过程中根据不同雷达测站的噪声加入了测量误差。
3)在精密定轨过程中由于弧段较短时不能进行精密定轨确定协方差,因此在一些卫星之间的关联模拟过程中选用了较长的弧段进行定轨,弧段长定轨协方差小,而马氏距离计算时协方差的逆较大,关联值较大。
假设选取精密的轨道根数作为真实轨道,短弧段情况下可以计算出轨道协方差,则关联阈值会大幅下降。
图5表示相同卫星不同历元间隔对应的关联量。可以看出,随着轨道时间间隔增加关联量逐渐下降,相同轨道时间间隔,不同卫星轨道所计算的关联量也不相同。关于关联阈值的选取需要针对不同卫星轨道做进一步的分析。
3 结束语
本文研究了基于协方差理论的UCTs动态关联算法,对比分析了基于雅克比转换的线性协方差演化方法和基于UT转换的UKF协方差演化方法。以400 km和1k500kkm轨道高度为例,初始轨道协方差相同的情况下,基于UT变换的协方差演化精度要高于基于雅克比转换的线性协方差方法演化精度。应用UKF方法轨道协方差演化一天的位置误差分别是分米量级和厘米量级,应用线性方法演化一天的位置误差是米级。
把协方差演化方法应用到UCTs动态关联中去,模拟印度一箭104星中的20颗卫星的轨道关联,当轨道关联量阈值选取为200时,20颗卫星轨道可以全部关联。
轨道协方差演化有很好的应用前景,本文在空间目标编目方面,为处理各非关联轨道提出了一种动态算法,其关联量源于每个非关联轨道的轨道误差协方差矩阵。另外空间目标碰撞评估的一个重要环节是计算两个空间物体的碰撞概率。碰撞概率的计算使用了相对状态概率密度函数的数值积分算法。每种算法需要为两个对象输入状态向量的误差信息。状态向量的误差信息通过协方差矩阵的方式来表示。本研究可以为将来的空间目标编目和空间碎片预警提供方法参考。
