拓扑模型在马氏体相变形状应变计算中的应用

（五邑大学 智能制造学部，广东 江门 529020）

合金马氏体相变属于位移型相变，它通过相界面处原子整体有序的“军事化”迁移完成母相至马氏体相结构之间的转变，此转变过程中产生的宏观变形（形状应变）是马氏体相变中一个十分重要的晶体学特征，也是工业生产中钢铁材料强韧化处理的基础. 特别地，马氏体相变形状应变还与一类应用广泛的智能材料如 NiTi的形状记忆效应密切相关. 因此，全面探索合金在马氏体相变过程中的形状应变特征有助于深入理解、合理控制材料微观组织，实现材料性能最大化. 文献[1]观察发现，马氏体相变产生的形状应变会导致预先抛光的合金试样表面产生皱纹或浮凸. 进一步地，若在该试样表面预先刻一直线划痕，则该刻痕在马氏体相变过程中将被折成若干段折线，且刻痕在母相与马氏体相界面或称惯习面处仍然保持连续，表明惯习面在马氏体相变过程中不发生畸变和旋转. 据此，Wechsler等[2]提出马氏体相变形状应变为不变平面应变，并通过矩阵代数和几何方法分别独立建立了马氏体相变晶体学唯象理论. 唯象理论是描述合金马氏体相变晶体学特征的经典理论，可计算得到马氏体惯习面、位向关系以及形状应变等重要晶体学特征参量，其正确性目前在大量合金中已得到充分验证. 然而，由于该理论自身的“唯象性”，因而无法给出母相与马氏体相界面的微观结构以及相变机制的合理解释. 众所周知，相界面结构对合金相变过程具有显著影响，进而制约合金的宏观性能，因此它在马氏体相变研究中具有相当重要的地位，如何合理地描述相界面结构特征是研究者们重点关注的问题. 基于文献[3-4]，Pond等[5-6]认为马氏体惯习面实际具有半共格台阶结构，并在此基础上建立了拓扑模型. 该模型从母相与马氏体相界面的微观结构出发，除了能预测合金马氏体相变晶体学特征参量之外，还可以计算表征相界面内的位错结构特征，据此可解释马氏体相变过程的微观机制.本文旨在基于拓扑模型推导并阐明马氏体相变形状应变的形变特征.

1 马氏体相变的拓扑模型简介

在光学显微镜下观察，合金的平直马氏体惯习面实际在原子尺度下具有如图1所示的台阶结构特征，其中惯习面与台阶面之间存在倾角ψ，而在台阶面上由于两相晶格类型及晶格常数间存在差异而产生晶格错配. 在拓扑模型中，母相和马氏体相在晶格形变E的作用下在台阶面上形成共格关系以降低晶格错配引起的弹性应变能，并称该晶格形变E为共格应变，同时拓扑模型通过引入两组界面位错阵列对共格应变E进行松弛：其中，一组界面位错称为相变位错[5-6]，它除了表现出一般位错特征外还具有台阶结构，记为，其中“h”表示台阶的高度；另一组界面位错称为晶格不变应变位错（Lattice invariant deformation dislocation，LID），通常为晶体位错，如滑移或孪生位错，LID位错迁移运动至惯习面的过程中不引起晶体结构的改变，记为，其中“0”表明该界面位错不含台阶特性. 拓扑模型基于相界面位错结构合理地描述了合金马氏体相变的无扩散性和微观转变机制，并将相变过程归因于相变位错在台阶面上的滑移，当相变位错划过母相晶体区域时原子从母相晶格阵点位置向马氏体相晶格阵点位置作有规律的军队式迁移从而实现母相向马氏体相晶体结构之间的转变.

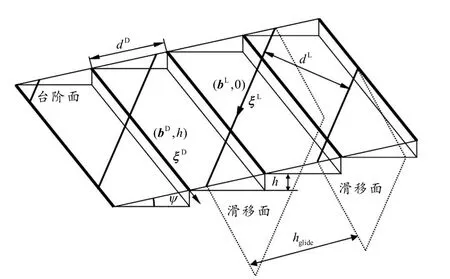
图1 拓扑模型中马氏体相与母相的相界面结构示意图

2 马氏体相变的形状应变

在拓扑模型中，马氏体相变的形状应变Γ包括塑性应变和静弹性应变两部分，其中塑性应变由相变位错和LID位错在合金晶体内滑移运动产生，而静弹性应变则源于共格应变E以及惯习面两侧晶体的小角度（＜5°）刚性倾转[5-6]. 当相变位错在台阶面内滑移时，位错前沿母相向马氏体相晶体结构转变从而引起塑性变形. 根据位错运动滑出晶体外部所产生的形变公式，可以计算得到一组Burgers矢量为bD且等间距dD分布的相变位错阵列在高度为h的台阶面上滑移单位距离时所产生的塑性变形ΓD：

式中，nTP为台阶面单位法线. 进一步地，以相变位错线方向ξD和惯习面法线为x和z轴建立惯习面坐标系，则式（1）展开可得：

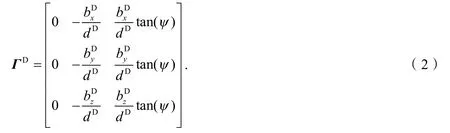
类似地，在相变位错滑移的同时，LID位错沿其滑移面运动至惯习面并产生塑性变形ΓL，则：

式中，nglide为LID位错滑移面单位法线，hglide为LID位错滑移面间距. 将式（3）在惯习面坐标系中展开可得：

除了上述界面位错运动引起的塑性变形之外，共格应变E对形状应变也有贡献. 根据前述可知，共格应变E通过惯习面内恰当取向及等间距分布的相变位错和LID位错阵列完全松弛或吸收，且界面位错的线方向、间距与共格应变E满足Frank-Bilby公式[7-8]：

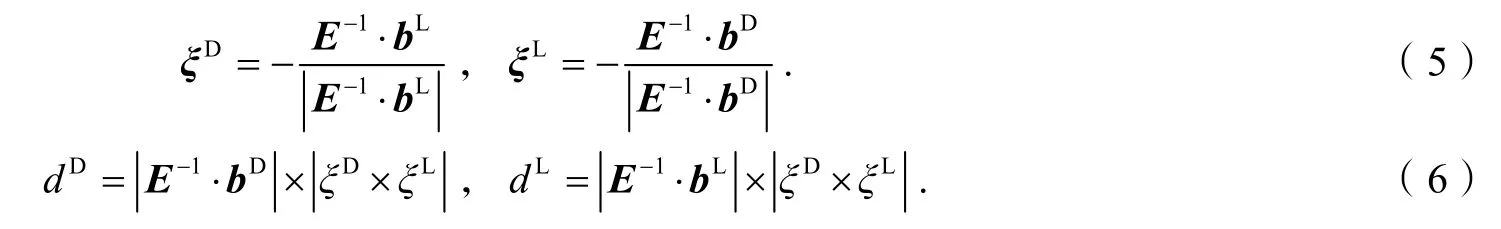
据此，通过矩阵代数可得到共格应变E在惯习面坐内的应变分量EHP与界面位错的线方向和间距之间具有如下关系：

进一步地，对比式（7）与式（2）和（4）之和可以推断：界面位错运动产生的塑性应变量与共格应变E在惯习面上相互抵消，即塑性应变 (ΓD+ΓL)与共格应变E之和具有如下形式：

此外，相变位错和LID位错Burgers矢量垂直于惯习面的位错分量bz对共格应变E的松弛不产生作用，相反，该位错分量阵列引起惯习面两侧母相和马氏体相晶体分别发生以位错线方向为轴的小角度刚性倾转. 根据Hirth和Lothe位错阵列弹性应变理论[9]，相变位错Burgers矢量分量引起的晶体刚性旋转矩阵在惯习面坐标系中可表示为：

对比式（8～10）可知，式（8）中的剪切应变εzx和εzy被界面位错 Burgers矢量垂直于惯习面分量引起的晶体旋转RD和RL所松弛.

综上，得到拓扑模型中马氏体相变形状应变Γ在惯习面坐标系下具有如下矩阵形式：

由式(11)可以看出，当母相和马氏体相之间的晶格错配被相变位错和LID位错阵列完全松弛时，宏观形状应变Γ具有不变平面应变的特征，它包含一个平行于惯习面的剪切形变和一个垂直于惯习面的轴向应变，其中应变分量εxz和εyz表征剪切形变，轴向应变εzz描述马氏体相变引起的合金体积变化. 换句话说，拓扑模型求解得到的马氏体惯习面在相变过程中没有发生畸变和旋转，即“不变平面”特性，满足划痕实验结果，与经典唯象理论中的不变平面假设一致. 一般地，唯象理论利用有限变形理论定量表征马氏体相变过程中的晶体形变，缺乏对惯习面微观结构包括界面位错特征及其近邻应力应变场的考虑和分析，因而唯象理论中的“不变平面”实际只具有几何意义. 另一方面，拓扑模型根据相界面的实验观察结果，直接分析讨论马氏体惯习面微观结构特征，并基于相变位错运动过程解释马氏体相变中的结构转变行为，进而阐明马氏体相变形状应变为实际界面位错滑移运动引起的晶体塑性变形以及其自身静弹性应变场共同作用的结果. 因此，相比于唯象理论，拓扑模型在对马氏体相变形状应变的描述上更具物理意义及普适性.

3 结论

本文在拓扑模型框架下分析讨论了合金马氏体相变引起的形状应变，并推导得到形状应变的矩阵分析表达式，它具有“不变平面应变”特征，与表面划痕实验的观测结果一致，据此验证了拓扑模型理论方法的有效性和可靠性. 本文方法可应用于表征陶瓷材料如二氧化锆相变增韧过程中马氏体相变所伴随的形状和体积变化以及NiTi形状记忆合金回复形变和回复力的定量计算中.

此外，基于马氏体相变过程以及其晶体学特征的多样性及复杂性，我们下一步工作将对形状应变产生的微观机理进行探索，拟借助分子动力学模拟手段在原子尺度下揭示马氏体的相变本质，进而剖析其宏观体积的变化规律.