一类亚纯双单叶函数类的系数估计
2019-01-19
五邑大学学报(自然科学版) 2018年4期
(滁州职业技术学院 基础部,安徽 滁州,239000)
1 引言及预备知识
令H表示在内具有下述形式的解析函数类

S表示H中的单叶函数族.

每个具有形式(1)的亚纯单叶函数f∈∑都存在逆函数f,定义为

这里

如果函数f和f-1都在U*单叶,则称函数f∈∑在U*内亚纯双单叶函数. 现记σ表示单位圆U*所有具有(1)式的亚纯双单叶函数. 近来,许多作者[1-5]研究了亚纯双单叶函数类.
定义 1令. 如果f(z)满足

其中λ≥0,g(w)=f-1(w),φ(z)=1+B1z+B2z2+…(B1>0),则称f(z)∈∑(λ,φ).
为了得出我们的结论,需要如下的定理.
引理 1[6]设内的正实部函数,则

引理 2[7-8]设内的正实部函数,则存在复数x,y,且x|≤ 1 ,|y|≤ 1 使得
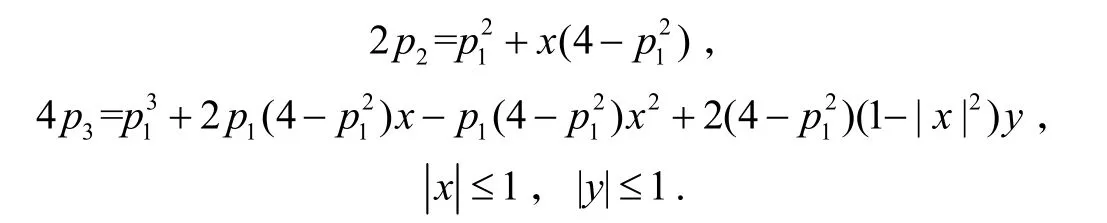
2 主要结果及证明
定理假设f(z)∈∑(λ,φ) ,则有
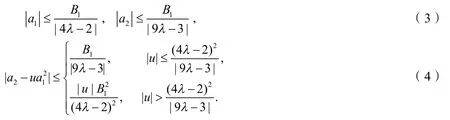
证明因为f(z)∈∑(λ,φ) ,则存在u(z),v(w)(u(0)=v(0)),满足
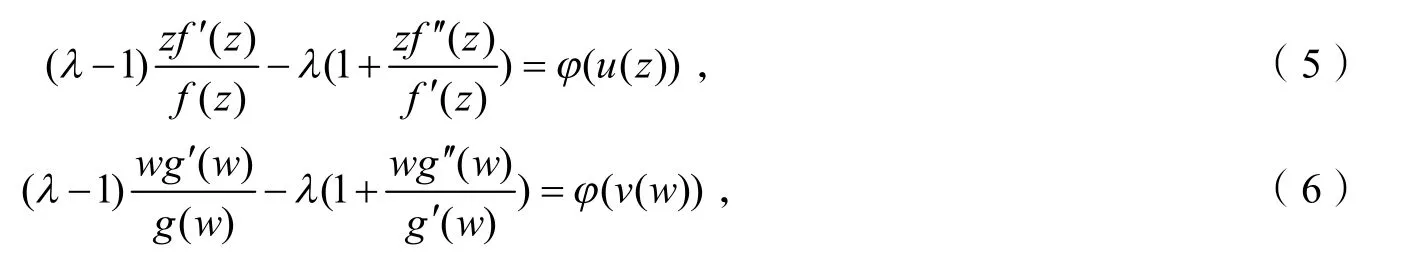
其中

由式(7)、(8)得

所以有

由式(11)、(12)、(13)和(14),得p1=q1= 0 ,及

所以有p2=-q2,p3=-q3.
由引理1得

由式(15)、(16)得

由引理2存在复数x,y(|x|≤1,|y|≤1),使得p2=2x,p3=2(1-|x|2)y,则式(19)变为
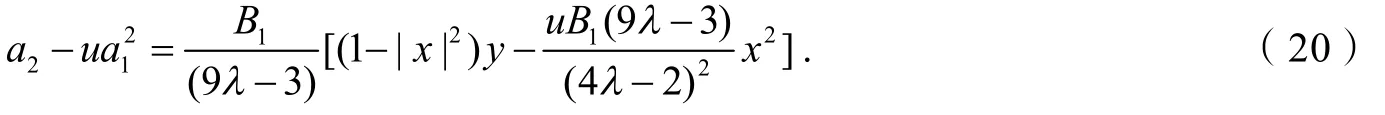

所以


3 推论
推论1假设f(z)∈∑(0 ,φ),则有
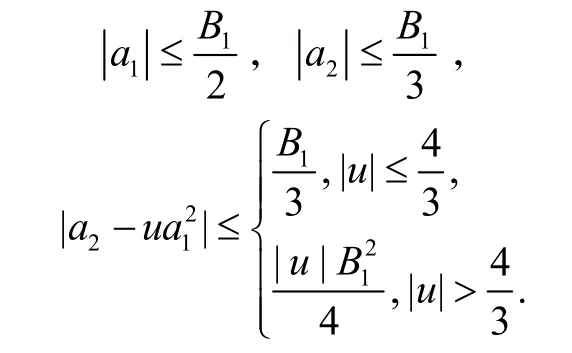
推论2假设f(z)∈∑(1 ,φ),则有