An Elementary Fractal Thermal Conduction Theory Model for Nanometer Energetic Materials
2019-01-19WANGYiSONGXiaolanHUANGHaoLIFengsheng
WANG Yi, SONG Xiao-lan, HUANG Hao, LI Feng-sheng
(1.School of Materials Science and Engineering, North University of China, Taiyuan 030051, China; 2.School of Environment and Safety Engineering, North University of China, Taiyuan 030051, China; 3.China North Industries Group Corporation Limited, Beijing 100821, China; 4.School of Chemical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)
Abstract: Based on fractal theory and heat conduction theory, the correlation among sensitivity, heat conduction, and fractal dimension of energetic materials were analyzed. Meanwhile, the fractal heat conduction models of micro and nano energetic materials were established. To verify the correctness of the model, the size fractal dimension and surface fractal dimension of two kinds of nitroamine explosives with different particle size were calculated, and the thermal conductivity was calculated by the model. The results show that the tangential effective thermal conductivity (kt) and radial effective thermal conductivity (kr) of nano RDX were higher by 0.204 and 0.059W/mk than kt and kr of raw RDX, respectively. The kt and kr of nano HMX were higher by 0.079 and 0.426W/mK than kt and kr of raw HMX, respectively. This meant that nano energetic materials were of higher effective thermal conductivity than micron energetic materials, which quite benefited to dissipating of the heat and decreasing of temperature of hot spots. Thus, nano energetic materials exhibited lower sensitivities. It is also concluded that the sensitivity of energetic materials can be assessed by means of the models.
Keywords: nanometer energetic materials; fractal theory; thermal conduction models; RDX; HMX
Introduction
Particle size of energetic materials, size distribution, and morphology are important factors affecting sensitivity. The influence of particle size on sensitivity of energetic materials has been reported[1-4]. When external stimulations (such as mechanical energy, electric energy, laser energy, and more) act on energetic particles, the stimulating energies change into heat energy within the particles. By conduction, the heat energy is transferred to adjacent energetic particles of various sizes and size distributions. Heat energy is also transferred to the surroundings. If the heat generation rate is faster than the heat dissipation rate, heat accumulates. Hot spots leading to an explosion (or combustion, or deflagration) may generate[5]. The essence of explosion (or combustion) of energetic materials can be attributed to the thermal conductivity of energetic particles, as well as their different particle sizes, size distribution, and morphology.
Generally, the particle size distribution and morphology of energetic materials prepared by same method have the self similarity of the scale free range, which can be characterized by fractal theory[6]. The thermal conduction of fractal energetic particles relates to chemical properties, size distribution, thickness ratio, complexity of particle shapes, heterogeneity of particle size, particle surface roughness, and specific surface area, and more[7-10]. Consequently, the size and surface fractal characteristics of energetic particles influence the heat conduction and sensitivity. In this paper, it is first proposed that the qualitative and quantitative fractal thermal conduction models of for energetic materials. They link the thermal conduction and the sensitivity of energetic materials with the particle size fractal dimension (Dg) and surface fractal dimension (Ds). Experimental data is used to verify the model.
1 Physical meaning of size fractal dimension
In Euclidean geometry, the dimension of space is the number of independent coordinates or the number of independent directions needed to determine the position of any point in the space. A point is zero dimensional, a line is one-dimensional, a plane is two-dimensional, a body is three-dimensional[11-12]. However, the geometry of the objective world is a complex system of irregularities and discontinuities. The dimensions of Euclidean geometry cannot describe complexity and irregularity of an object in the space.
Nevertheless, the dimension is continuous and can be an integer in fractal geometry. Fractal theory is an abstract description of irregularities and discontinuities of objects in the space. Fractal dimension is a quantitative parameter describing the complexity of an irregular complex system. It measures ability to fill the space of a fractal system. Fractal dimension describes the disorder of a fractal system by measurement theory and symmetry theory. Fractal theory provides a scientific concept and methodology for characterizing the irregularity and complexity in nature[13-14].
Generally, there are four characteristics of fractal geometry. First, fractal geometry has fine structure. That is, it contains the whole in any small scale (i.e., the self similarity in the scale-free interval)[12]. Second, fractal geometry is irregular and cannot be fully and accurately described by Euclidean geometry. Third, fractal geometry has similar or statistical self similar features. Finally, fractal dimension is usually larger than its topological dimension. In most cases, the fractal geometry is generated by a very simple recursive method[15-17].
Engineering practice shows that the particle size distribution prepared by the same grinding machine presents G-S distribution or the approximate R-R distribution. The two kinds of distributions are fractal distribution[18-20]. In this paper, the relationship of the frequency (YN) to the size (r) of energetic particles prepared by the same method is:
YN(r)=1-N-1n0(r/rmax)-D
(1)
In the formula,YNis the ratio of Nr(the number of particles with the size less thanr) toN(total particle number).rmaxis the largest particle size. Equation (1) can be reduced to a power law relation:
YN(r)∝-r-D
(2)
Equation (3) is the differential form of Eq. (2):
dYN(r)∝r-1-Ddr
(3)
The particles number from r tor+dr(dN) can be written as:
dN=NdYN(r)
(4)
Then, the particles mass fromrtor+dr(dW) can be written as:
dW=ρKVr3NdYN(r)
(5)
In the formula,ρis the particle density,Kvis the shape factor. In addition, dWcan be written as:
dW=WdYW(r)
(6)
In the formula,Wis the total particle mass.Yw(r) is the ratio of the mass of particles less thanrtoW, combining Eq. (5) with Eq. (6):
dYW(r)=ρN(KV/W)r3dYN(r)
(7)
Substituting Eq. (3) into Eq. (7):
dYW(r)∝r2-Ddr
(8)
The integration of differential Eq. (8) gives:
YW(r)∝r3-D
(9)
Using the proportional relation of the particle volume to particle mass, equation (9) may be written as:
YV(r)∝r3-D
(10)
In this study, the cumulative distribution curves of energetic material belonging to a G-S or R-R distribution, is shown in the simplified form as:
YV(r)∝rb
(11)
If the graph of the cumulative distribution curve of energetic materials in the double logarithmic coordinates (lnYv(r)-lnr) graph is a straight line, the slope of the line isb. Then the particle size fractal dimensionDgof the energetic material is:
Dg=3-b
(12)
Particle size fractal dimensionDgis a parameter characterizing the complexity and heterogeneity of energetic material. With the cumulative distribution curve of the energetic sample, theDgvalue can be determined. The cumulative distribution function can be expressed as:
Y(r)=kr3-D
(13)
Assume two cumulative distribution curves (Y1andY2) with differentDgvalues (see Fig. 1(a))[21]. TheY2is shifted to the left and is coincident withY1at a cumulative percentage of 100% (Fig.1(b)). The distribution ofY1is wider thanY2. The cumulative distribution functions ofY1andY2are:
Y1(r)=k1r3-D1
(14)
Y2(r)=k2r3-D2
(15)
Writing these equations in logarithmic form:
lnY1(r)=(3-D1)lnr+lnk1
(16)
lnY2(r)=(3-D2)lnr+lnk2
(17)
The double logarithmic graphs (lnY-lnr) are shown in Fig.1(c). The slope ofY2is greater than that ofY1. That is, 3-Dg2>3-Dg1. SoDg1>Dg2.
It is found that theDgvalue is closely related to the width of particle size distribution. The physical meaning of particle size fractal dimension has three points. First, the theoretical value ofDgis in the range of 0 to 3. Substantial statistical results show that theDgvalue falls between 1 and 3. The limit point,Dg=0, means that all particles are the same size. Then the particles are not fractal. AsDgapproaches 0, the particle sizes become more uniform in size. Second, the larger the value ofDg, the wider the particle size distribution. Finally, when the size distribution range is the same, the larger the value ofDg, the larger the proportion of the smaller particles and the more complex the energetic particles.
2 Calculations of size fractal dimension
2.1 Size fractal dimension of micron and nano RDX
The particle size distribution of the energetic materials was analyzed with a Master Sizer laser analyzer, made in Malvin, England. The size cumulative distribution, the size frequency distribution, and relative data of energetic materials are obtained. The least squares method was used to fit the log data (lnY, lnr) from the size cumulative distribution data (Y,R). If there is a straight line, then the slope isb. The particle size fractal dimension (Dg) is 3-b.
TheDgvalues of raw RDX and nano RDX calculated according to the results of particle size analysis shown in Fig.2. From the Figure 2(a), the average particle size (d50) of raw RDX is 17.45μm. TheDgvalue is calculated as 2.033 by linear fitting of double log data (lnYv, lnr) of the size cumulative distribution of raw RDX. TheDgvalue of nano RDX from the size cumulative distribution is 0.431,d50is 0.18μm. The smaller the set of cumulative distribution data, the smaller the linear correlation coefficient (R).
2.2 Size fractal dimension of micron and nano HMX
TheDgvalues of raw HMX and nano HMX are calculated with the size cumulative distribution data (Fig.3). Thed50value of raw HMX (Fig.3(a)) with a wide size distribution is 147.33μm. Linear fitting of the HMX double log data (lnYv, lnr) of the size cumulative distribution curve (Fig.3(b)), leads toDg=1.965, slightly smaller than RDX. For nano HMXDg=0.817 andd50=0.21μm, larger than nano RDX.
3 Fractal thermal conduction models for energetic particles
3.1 Qualitative fractal thermal conduction model
Thermal conductivity of energetic particles is assumed to be related to the specific surface area (Sm) and the particle size fractal dimension (Dg). When theDgvalue is large, the proportion of the small particles is large. Consequently the total specific surface of sample of energetic material is larger than a sample with fewer fine particles because smaller particles have larger specific surface area than larger particles. Heat will more quickly dissipate to the surroundings as the number of smaller particles in the size distribution increases. Faster dissipation of the heat energy discourages the appearance of hot spots. The qualitative fractal thermal conduction model establishes the role of particle size fractal dimension (Dg) on the effective thermal conductivity (keff) of energetic materials.
The qualitative model has three computational steps. First, the probability of the particles frommtom+dm(ymdm) can be expressed by the relationship of the particle mass (m), the particle size (r) and the frequency (YN):
(18)
Second, according to the kinetic theory of dense gas and energy conservation equation, the average heat flux in theYdirection (Qy) of the energetic particles can be deduced by:
(19)
Third, by combining the formula (18), (19) and Fourier theoremkeffof energetic materials is:
keff=-Qy/(dT/dy)
(20)
In this model, assuming the spherical particles with smooth surface and different sizes, the mass of any particle is:
(21)
Due to the size-frequency relation, theymdmcan also be written as:
(22)
Consequently,Qycan be calculated by the formula (23):
(23)
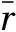
Thus, thekeffof energetic materials can be calculated by the formula (24):
(24)
Here,βis a vital parameter characterizing the influence of the fractal characteristics on the heat conduction of energetic materials. It is closed related with such parameters asη,DgandDs. In the model,βis expressed by the formula (25):
(25)
The parameterηis the structure parameter of energetic particles, which represents the proportion of the maximum particle to the total particles number. It can be expressed by the formula (26):
η=n0/N
(26)
Obviously, that 0<η≤1. Whenηequals to 1, it means that the size of any particles is homogenous. Whileηtends to 0, the energetic particles become to a fractal system with extremely complex size distribution.
In summary, the effective thermal conductivity varies with the parameters ofDg,η,v,ρandCpas shown in Fig.4[22].
The routine sensitivity tests of explosives involve the impaction, the friction and the thermal decomposition. The solid volume percentage (v) of energetic materials can be demonstrated as follows. When the conditions such as the mass of charge, the charge density and the loading force, etc, are the same in a test, the initialvvalue is a fixed value, and the Δvvalue should be also a fixed value after mechanical stimulation. In the thermal decomposition test, thevvalue of the energetic materials remained unchanged.
3.2 Quantitative fractal thermal conduction model
The above qualitative fractal heat conduction for energetic materials provides a method to estimate the thermal conduction by size fractal dimension. Herein, a quantitative fractal thermal conduction model is also proposed in which the effective thermal conductivity of energetic materials can be calculated with the fractal dimension. Therefore, the heat accumulation or heat dissipation, even the sensitivity of energetic materials can be determined by this model.
The following assumptions are in the quantitative fractal thermal conduction model. The energetic particles are fully dried, and the air is filled with the gap among the particles. Without consideration of the thermal convection and thermal radiation, the thermal conduction is only considered. Here, it is assumed a unit with the thickness ofb, the length of l, and with a cavity with the height ofh(shown in Fig.5[23]).Xrepents axial, andYradial.keis the thermal conductivity of explosives,kcis the thermal conductivity of cavity. The thermal resistance of the fractal energetic particles in tangential and radial directions is shown in Fig.6[23]
Assuming that the heat flow is parallel to theXaxis, the vertical thickness of the unit is l. The thermal resistance of each part of the unit is as formula (27):
(27)
Then, the total thermal resistance of the unit of the fractal energetic materials is as formula (28):
(28)
In the formula,ktis the tangential effective thermal conductivity. It can be replaced by formula (29):
(29)
Therefore,ktof the energetic materials can be written in formula (30):
(30)
When the heat flow is parallel to theYaxis, the thermal resistance of each part of the unit is as formula (31):
(31)
The total thermal resistance of the unit of the fractal energetic materials is as formula (32):
(32)
In the formula,kris the radial effective thermal conductivity. The total thermal resistance can be written as formula (33):
(33)
Accordingly, thekrof energetic materials can be shown as formula (34):
(34)
Based on the former assumptions, the ratio of cavity (Φ) is shown as formula (35):
Φ=Ac/A
(35)
In the formula,Acpresents the area of cavity;Apresents the area of the unit. They can be written as formula (36):
Ac=hl-2bhA=hl+2bl
(36)
By replacing formula (36) into formulae (30) and (34), formulae (37) and (38) are obtained respectively:
(37)
(38)
Additionally, the relationship betweenΦandDsis as formula (39). In the formula,Cis a constant:
Φ=CADs-1
(39)
Φcan be also calculated by formula (40):
Φ=1-(ρave/ρth)
(40)
In the formula,ρaveis the apparent density of energetic particles, andρthis the theoretical density of energetic particles. Commonly, theΦof bulk powder is statistically from 0.48 to 0.55. Here, assumingΦequals 0.51,A=4μm×4μm,Ac=3μm×3μm. ThenCequals to 2.22 by replacing these data into formula (39). Due toDg=Ds+1,Φcan be written to formula (41):
Φ=2.22×16Dg-2
(41)
The formulae (42) and (43) are obtained by replacing formula (41) into formulae (37) and (38) respectively:
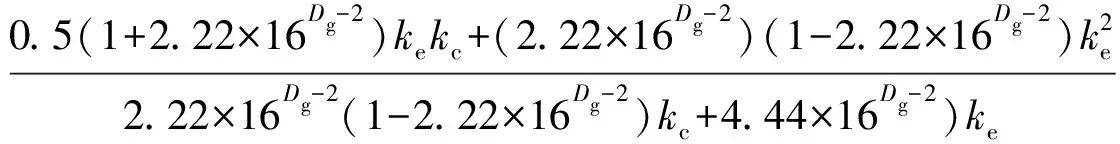
(42)
(43)
In the calculation,kcof air equals to 0.0256,keof explosives can obtained by some handbook. In this paper, the values ofktandkrof explosives were calculated with their size fractal dimensions and listed in Table 1. For comparison, the results are shown in Fig.7.

Table 1 Thermal conductivity calculation results of the four samples
Three conclusions can be drawn from the above results. Firstly, for the same explosive, with increase of the fractal dimension, the tangential and radial effective thermal conductivity decrease, and the fractal dimensions of nano explosives are obviously lower than those of micro explosives. The results show that the particle size distribution uniformity of nano explosives with low fractal dimension is good, which is favorable to the heat conduction and heat dissipation. Ultimately, it leads to the decrease of the sensitivity of the nano explosives. Secondly, compared with the same explosive, the tangential and radial effective thermal conductivity of nano samples is higher than that of micron samples. It indicates that nano explosives with nanosize effect, and larger specific surface, higher activity have the better heat transfer among the particles which result in rapid heat dissipation and little hot spots to initiate explosion. Thirdly, compared with the different explosives, the tangential and radial effective thermal conductivity of nano RDX are lower than that of nano HMX, respectively. The tangential and radial effective thermal conductivity of micro RDX are lower than that of micro HMX, respectively. It means that the thermal conduction of nano and micro RDX are lower than that of nano and micro HMX, respectively, which result in the thermal decomposition in advance, the higher mechanical sensitivity. The results of sensitivity tests are in good agreement with the above ratiocination, namely, the safety of HMX is higher than that of RDX. These results also verify the correctness of the model.
4 Conclusions
(1)The thermal conduction models for fractal energetic materials are proposed based on some assumptions, and are applicable to the bulk and fully dry energetic materials.
(2)The models fit the experimental data well for nano energetic materials, by means of which, we can investigate the thermal conduction and sensitivity of energetic materials in air.
