极坐标系下的面积元素推导
2019-01-18仇海全
潘 花 仇海全
(安徽科技学院数学系, 安徽 凤阳 233100)
在高等数学理论中,极坐标可用于计算二重积分[1]。在各类高等数学教材中,通常根据二重积分的定义[1],即特殊“和式”的极限,通过分割积分区域、近似替换、求和、取极限等步骤,得出极坐标系下面积元素的表达形式。这种表达方式过于抽象,学生不易很快掌握。在此给出一种推导方法,更直观地阐述极坐标系下面积元素表示的基本概念,帮助学生理解和掌握。
1 常用的极坐标系下面积元素的推导方法
二重积分的定义式为[1]:
在大多高等数学教材中,介绍极坐标系下面积元素的表示时,首先介绍积分区域D的分割[1]。如图1所示,将区域D任意分割成n个小区域,从中任取一小区域,将其面积记为Δσi。
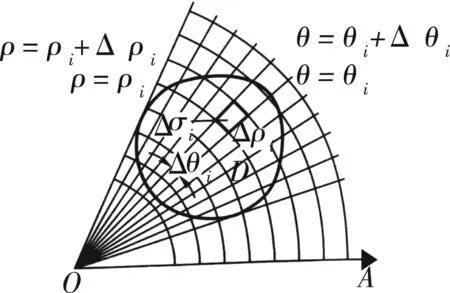
图1 常见积分区域分割
近似替换小区域的面积:

令
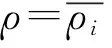
对所有小区域的面积求和,得到整个积分区域面积的近似表达式;最后,对得到的和式取极限,则有

最终得到极坐标系下二重积分的表示形式[1]:

其中,ρdρdθ即极坐标系中的面积元素。
在杨慧卿编著的教材中[2],采用的分割方法与上述方法相同,分割图形如图2所示。在分割得到的小区域中,任意选取小区域Δσ,将该小曲边四边形的面积用长方形的面积近似表示为Δσ≈rdrdθ[2],由此得到极坐标系下的面积元素。
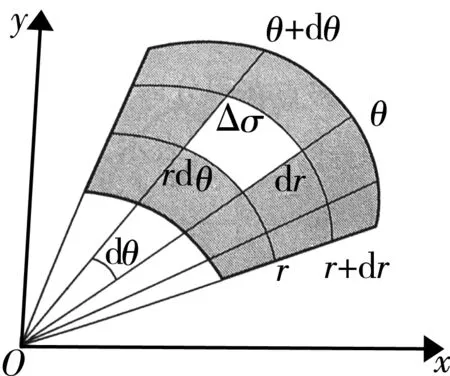
图2 分割积分区域得到四边形区域Δσ
前述推导方法中,在讲解极坐标系下分割积分区域时,都未进一步解释采用该方法的原因。数学基础较差的学生,经常会将其与直角坐标系下所采用的两族平行直线分割积分区域的方式相混淆,从而对2种坐标系下面积元素的表示形式认识不清。
颜刚等人简要介绍了直角坐标系下和极坐标系下积分区域的分割方法[3],但未对采用这种分割方法的原因进行说明。
因此,有必要对直角坐标系下分割积分区域的方式进行具体阐述,将2种坐标系下面积元素表示形式区分开来,帮助学生加深理解。
2 积分区域分割方法的实质
2.1 直角坐标系下所用分割方法的实质
根据二重积分的定义可知,积分区域的分割方式是任意的。在直角坐标系中,为得到面积元素的表示形式,采用了特殊的分割方法 —— 用两族平行于坐标轴的直线分割积分区域(见图3)。通常,平行于y轴的直线可表示为:x=常数;平行于x轴的直线可表示为:y=常数。在直角坐标系下,用两族平行于坐标轴的直线分割积分区域,实质上是用坐标分量为常数的线来分割积分区域。这样分割得到的小区域,除了含边界线的小区域以外,其他小区域都是长方形区域。根据定积分的元素法[4],设其中任一小长方形的长为dx,宽为dy。根据长方形的面积计算公式,即可得到直角坐标系下的面积元素:dσ=dxdy。

图3 用两族平行于坐标轴的直线分割积分区域D
2.2 极坐标系下所采用的分割方法
若在极坐标系中采用与直角坐标系中相同的分割方法,分割得到的小区域在极坐标系下难以计算面积。在直角坐标系下,分割积分区域的方法实质是用坐标分量为常数的直线来分割积分区域D。因此,在极坐标系下,也采用坐标分量为常数的线来分割积分区域D。
在极坐标系中:坐标分量θ为常数,表示以极点O为端点的一族射线;坐标分量ρ为常数,表示以极点O为圆心的一族同心圆。用坐标分量ρ、θ为常数的线分割积分区域D,所得图形如图4所示。在分割积分区域D后所得到的小区域中,除了含边界线的小区域以外,其他小区域都是由2条射线和2个圆弧所围成的闭区域,该小区域的面积可以由2个扇形面积之差来求解。
3 极坐标系下面积元素的推导过程
假设从极点O出发且穿过闭区域D内部的射线与D的边界曲线相交不多于2点[1],用坐标分量ρ、θ为常数的线来分割积分区域D,任取一小块闭区域。如,由射线θ与射线θ+dθ,以及圆弧ρ与圆弧ρ+dρ围成小块闭区域,其面积记为Δσ(见图5)。
图4 用坐标分量为常数的线分割积分区域D

图5 小块闭区域面积Δσ
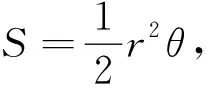
整理后得:
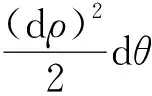
由此可见,二重积分的面积元素dσ与坐标系有关。 因此,不能因为直角坐标系下的面积元素dσ=dxdy,而错误地认为极坐标系下的面积元素为dσ=dρdθ。 面积元素dσ在直角坐标系下的表示形式与在极坐标系下的表示形式有所不同,不能简单地理解为dxdy=ρdρdθ。
根据直角坐标与极坐标的关系,以及全微分的运算法则,可得:
dx=d(ρcosθ)=cosθdρ-ρsinθdθ
dy=d(ρsinθ)=sinθdρ+ρcosθdθ
从而得到:
dxdy=(cosθdρ-ρsinθdθ)·(sinθdρ+ρcosθdθ)
=sinθcosθ(dρ)2+(cos2θ-sin2θ)ρdρdθ-
ρ2sinθcosθ(dθ)2
4 结 语
从直角坐标系下积分区域分割方法的本质特征出发,给出极坐标系下面积元素的一种推导方法。该方法的推导过程更加直观形象,应用于高等数学教学当中,更利于学生快速理解和熟练掌握。通过提出问题、解决问题的数学方法,引导学生积极思考,变被动学习为主动学习,培养学生分析问题的能力,有助于教学效果的提高。
