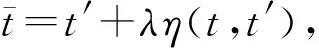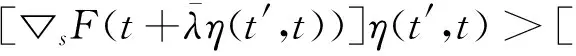n维模糊映射的s-预不变凸性及其优化
2019-01-18白玉娟张丽丽
白玉娟, 张 琛, 张丽丽
(陇东学院 数学与统计学院, 甘肃 庆阳 745000)
自从美国加州大学控制论专家Zadeh教授1965年提出模糊集的概念以来,模糊数学作为一门新的数学学科得到了迅速的发展.经典凸分析理论与数学规划等应用模型的研究是息息相关的.然而,正如许多系统中含有参数的不确定性,在优化理论中往往在目标函数、约束条件、目标函数与约束条件中同时带有参数的不确定性,从而使模糊优化问题已有很多的讨论,并促使了模糊凸分析理论的研究.关于模糊映射的凸性、拟凸性及B-凸性,一些文献已有讨论.1994年,Noor[1]提出预不变凸模糊数值函数的概念,并讨论了模糊数值函数的预不变凸性;2016年,Gong等[2]在定义n维模糊数空间偏序关系的基础上,对n维模糊映射的凸性进行了系统研究,但对n维模糊映射广义凸性的本质研究还需进一步深入.本文利用n维凸模糊数值函数的一些研究,首先提出n维模糊数值函数的s-不变凸、严格s-不变凸、s-预不变凸和半严格s-预不变凸的概念,其次利用n维模糊数值函数依支撑函数的可微性与梯度讨论以上广义凸性的关系,最后建立模糊优化问题(FMP)的最优化条件.
1 预备知识
定义1.1[3]设u∈F(Rn),若u满足以下性质:
1)u是一个正规模糊集,即存在x0∈Rn使得u(x0)=1;
2)u是一个凸模糊集,即对∀x,y∈Rn,λ∈[0,1],u(λx+(1-λ)y)≥min{u(x),u(y)};
3)u是上半连续函数,即[u]r={x∈Rn:u(x)≥r}是闭集,其中r∈(0,1];
4)u的支集suppu的闭包
是紧集,则称u为n维模糊数构成的n维模糊数空间记为En.
当r=1时,称[u]1={x∈Rn:u(x)=1}为模糊数u的核.
定理1.1[4](n维模糊数表示定理) 设u∈En,则:
1) 对任意r∈(0,1],[u]r均为Rn上的非空紧凸集;
2) 若0≤r1≤r2≤1,有[u]r2⊂[u]r1;
3) 若正数列rn非降收敛于r∈(0,1],有
反之,若对任意的r∈(0,1],均存在Ar⊂Rn,满足上述条件1)~3),则存在唯一的模糊数u∈En,使得对任意的r∈(0,1],均有[u]r=Ar且
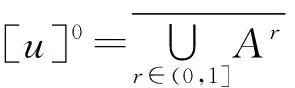
模糊数的加法和数乘运算定义如下:设u,v∈En,k,k1,k2∈R,则

k(u+v)=ku+kv,
k1(k2u)=(k1k2)u,
(k1+k2)u=k1u+k2u,k1k2≥0,
[u+v]r=[u]r+[v]r=
{x+y:x∈[u]r,y∈[v]r},
[ku]r=k[u]r={kx:x∈[u]r}.
定义1.2[5]对模糊数u∈En,称
为u的支撑函数,其中I=[0,1],x∈Sn-1是Rn上的单位球面,即
Sn-1={x∈Rn:‖x‖=1},

定理1.2设u∈En,r∈[0,1],x∈Sn-1,则
[u]r={y∈Rn:〈y,x〉≤u*(r,x),
x∈Sn-1,r∈[0,1]}.
定理1.3设u∈En,则:
1)u*(r,x+y)≤u*(r,x)+u*(r,y);
2)u*(r,x)在I×Sn-1上一致有界,且
3) 对任意的x∈Sn-1,u*(r,x)关于r非增左连续且在r=0处右连续;
4) 对任意的r∈[0,1],u*(r,x)关于x一致Lipschitz连续,且

5) 对任意的r∈[0,1],u,v∈En,
6) (u+v)*(r,x)=u*(r,x)+v*(r,x);
7) (ku)*(r,x)=ku*(r,x),k≥0;
8) -u*(r,-x)≤u*(r,x);
9) (-u)*(r,x)=u*(r,-x).

则称F在t0点处可微,称模糊向量(u1,u2,…,um)为F在t0处的梯度,记作▽F(t0),即
▽F(t0)=(u1,u2,…,um).
注记1.1模糊映射F:M→En在t0点处的梯度▽F(t0)存在的充要条件是F(t)⊖gF(t0)存在且有
uj=


定义1.4[6]设u,v,ω∈En,若对任意的r∈[0,1],有
⊖gH[v]β),
其中⊖gH为非空紧凸集[u]β和[v]β的广义H-差,则称ω为模糊数u和v的广义差,记为u⊖gv=ω.
若对任意的t,t′∈M,∀λ∈[0,1],满足t′+λη(t,t′)∈M,则称M(⊂Rn)是关于η:Rn×Rn→Rn的不变凸集.
若对任意的t,t′∈M,∀λ∈[0,1],满足η(t,t′)+η(t′,t)=0,则称η:Rn×Rn→Rn为非对称映射.特别地,η(t,t′)=t-t′时,M退化为一般凸集.
条件K[7]设M(⊂Rn)是关于η:Rn×Rn→Rn的非空不变凸集,称η满足条件K,是指η对任意的t,t′∈M,λ∈[0,1],都满足以下条件:
(i)η(t′,t′+λη(t,t′))=-λη(t,t′);
(ii)η(t,t′+λη(t,t′))=(1-λ)η(t,t′).
2 n维模糊映射的s-预不变凸性及其优化
定义2.1设u,v∈En,如果对任意的r∈[0,1],x∈Sn-1,u*(r,x)≤v*(r,x),则称v依支撑函数优于u,记为u≼sv.如果u≼sv且存在r0∈[0,1],使得u*(r0,x) 对r∈[0,1]和x∈Sn-1一致成立,则称F在t0点处依支撑函数可微,称模糊向量(u1,u2,…,um)为模糊映射F在t0点处依支撑函数的梯度,记作▽sF(t0),即▽sF(t0)=(u1,u2,…,um). 注2.1模糊映射F:M→En在t0点处依支撑函数可微的梯度▽sF(t0)存在的充要条件是存在uj∈En(j=1,2,…,m),使得 定义2.3设M⊂Rn关于η:Rn×Rn→Rn是不变凸集,F:M→En为M上的n维模糊映射,则: 1) 如果对∀t,t′∈intM有 F(t)*(r,x)-F(t′)*(r,x)≥ [▽sF(t′)]η(t,t′) 对r∈[0,1]和x∈Sn-1一致成立,则称F在不变凸集M上关于η是依支撑函数不变凸模糊映射(简称为s-不变凸); 2) 如果对∀t,t′∈intM,t≠t′有 F(t)*(r,x)-F(t′)*(r,x)>[▽sF(t′)]η(t,t′) 对r∈[0,1]和x∈Sn-1一致成立,则称F在不变凸集M上关于η是依支撑函数严格不变凸模糊映射(简称为严格s-不变凸); 3) 如果对∀t,t′∈intM及∀λ∈[0,1],有 F(t′+λη(t,t′))*(r,x)≤ λF(t)*(r,x)+(1-λ)F(t′)*(r,x) 对r∈[0,1]和x∈Sn-1一致成立,则称F在不变凸集M上关于η是依支撑函数预不变凸模糊映射(简称为s-预不变凸); 4) 如果对∀t,t′∈intM,F(t)*(r,x)≠F(t′)*(r,x)及∀λ∈(0,1),有 F(t′+λη(t,t′))*(r,x)< λF(t)*(r,x)+(1-λ)F(t′)*(r,x) 对r∈[0,1]和x∈Sn-1一致成立,则称F在不变凸集M上关于η是依支撑函数半严格预不变凸模糊映射(简称为半严格s-预不变凸). 定理2.1设F:M→En在不变凸集M上处处依支撑函数可微,且▽sF(t)=(u1,u2,…,um).如果F在M上关于η是s-不变凸的,且η满足条件K,则F在M上关于相同η是s-预不变凸的. 证明当λ=0时,定义2.3中的不等式显然成立; 当λ=1时,由F(t)*(r,x)关于η的s-不变凸性和条件K,有 F(t)*(r,x)-F(t′+η(t,t′))*(r,x)≥ [▽sF(t′+η(t,t′))]η(t,t′+η(t,t′))=0, 即 F(t′+η(t,t′))*(r,x)≤F(t)*(r,x) 满足定义2.3中的不等式. 由于F(t)*(r,x)关于η的s-不变凸性,得到: 将上面2式分别乘以λ和(1-λ),然后相加得到 λF(t)*(r,x)+(1-λ)F(t′)*(r,x)- λF(t)*(r,x)+(1-λ)F(t′)*(r,x), 即证明当λ∈(0,1)时,定义中的不等式成立.综上,F(t)*(r,x)在M上关于相同η是s-预不变凸的. 定理2.2设F:M→En在不变凸集M上处处依支撑函数可微,▽sF(t)=(u1,u2,…,um),▽sF(t′)=(v1,v2,…,vm),且η满足条件K,F满足F(t+η(t′,t))*(r,x)=F(t′)*(r,x),∀t,t′∈intM,则F在M上关于η是半严格s-预不变凸的充分必要条件是 F(t)*(r,x)≠F(t′)*(r,x), ∀t,t′∈intM, 有 [▽sF(t)-▽sF(t′)]η(t,t′)>0, 即 对r∈[0,1]和x∈Sn-1一致成立. 证明假设F在M上关于η是半严格s-预不变凸的,则 F(t)*(r,x)≠F(t′)*(r,x), ∀t,t′∈intM, 于是有 F(t′)*(r,x)>F(t)*(r,x)+ [▽sF(t)]η(t′,t),F(t)*(r,x)> F(t′)*(r,x)+[▽sF(t′)]η(t,t′), 易得 [▽sF(t)-▽sF(t′)]η(t,t′)>0. 反过来,假设 F(t)*(r,x)≠F(t′)*(r,x), ∀t,t′∈intM, 有 [▽sF(t)]η(t′,t)-[▽sF(t′)]η(t,t′)<0. (1) 只需证 F(t′)*(r,x)>F(t)*(r,x)+ [▽sF(t)]η(t′,t). 反证法.设 F(t)*(r,x)≠F(t′)*(r,x), ∃t,t′∈intM, 使得 F(t′)*(r,x)≤F(t)*(r,x)+ [▽sF(t)]η(t′,t), (2) 由已知条件 F(t+η(t′,t))*(r,x)=F(t′)*(r,x), 有 F(t+η(t′,t))*(r,x)=F(t′)*(r,x)≤ F(t)*(r,x)+[▽sF(t)]η(t′,t). (3) 利用中值定理得到 F(t+η(t′,t))*(r,x)-F(t)*(r,x)= (4) 由(3)和(4)式有 [▽sF(t)]η(t′,t). (5) 下面分2种情况导出矛盾. (i) 如果 由(1)式得 并利用条件K,可推出 [▽sF(t)]η(t′,t)< 而这与(5)式矛盾. (ii) 如果 先证 若其不然,即 (6) 记 则由(6)式知φ(α)为常值函数,于是有 据上式和(4)式得 F(t)*(r,x)=F(t+η(t′,t))*(r,x). 同时注意到定理的假设条件 F(t′)*(r,x)=F(t+η(t′,t))*(r,x), 则 F(t)*(r,x)=F(t′)*(r,x), 这与已知F(t)*(r,x)≠F(t′)*(r,x)矛盾.因此 (7) 由(1)和(7)式得到: [▽sF(t+αη(t′,t))]η(t,t+αη(t′,t))+ [▽sF(t)]η(t+αη(t′,t),t)<0. 由条件K和上面2个不等式,可以推出: 由上面2个不等式并再次根据条件K,可以推出 由(4)式及上式得 F(t+η(t′,t))*(r,x)-F(t)*(r,x))> [▽sF(t)]η(t′,t). 由已知条件 F(t+η(t′,t))*(r,x)=F(t′)*(r,x), 有 F(t′)*(r,x)>F(t)*(r,x)+ [▽sF(t)]η(t′,t), 这与(2)式矛盾. 引理2.1设M⊂Rn关于η:Rn×Rn→Rn是不变凸集,且η满足条件K,n维模糊映射F:M→En在M上关于η是s-预不变凸的,任意固定t,t′∈intM,则 0<α<β≤1. 证明类似文献[8]中引理5.3.1的证明. 定理2.3设M⊂Rn关于η:Rn×Rn→Rn是开不变凸集,且η满足条件K,F:M→En在不变凸集M上处处依支撑函数可微,则F在M上关于η是严格s-预不变凸的充分必要条件是F在M上关于相同η是严格s-不变凸的,即∀t,t′∈intM,t≠t′,有 F(t)*(r,x)-F(t′)*(r,x)> [▽sF(t′)]η(t,t′)>0. 证明假设F在M上关于η是严格s-预不变凸的,据定义∀t,t′∈intM,t≠t′,有 F(t′+λη(t,t′))*(r,x)< λF(t)*(r,x)+(1-λ)F(t′)*(r,x). 由此 F(t)*(r,x)-F(t′)*(r,x), ∀λ∈(0,1). 据此和引理2.1知 [▽sF(t′)]η(t,t′)= F(t)*(r,x)-F(t′)*(r,x), 因此有 F(t)*(r,x)-F(t′)*(r,x)> [▽sF(t′)]η(t,t′). 反过来,假设∀t,t′∈intM,t≠t′,λ∈(0,1),由F关于η是严格s-不变凸的,据定义有: F(t)*(r,x)-F(t′+λη(t,t′))*(r,x)> [▽sF(t′+λη(t,t′))]η(t,t′+λη(t,t′)), F(t′)*(r,x)-F(t′+λη(t,t′))*(r,x)> [▽sF(t′+λη(t,t′))]η(t′,t′+λη(t,t′)). 以上2个不等式的两端分别乘以λ和(1-λ),相加得到 λF(t)*(r,x)+(1-λ)F(t′)*(r,x)- F(t′+λη(t,t′))*(r,x)> [▽sF(t′+λη(t,t′))][λη(t,t′+λη(t,t′))+ (1-λ)η(t′,t′+λη(t,t′))]. 利用条件K,有 λη(t,t′+λη(t,t′))+ (1-λ)η(t′,t′+λη(t,t′))=0, 所以有 F(t′+λη(t,t′))*(r,x)< λF(t)*(r,x)+(1-λ)F(t′)*(r,x), 即知F关于η是严格s-预不变凸的. 设模糊映射F(t),G1(t),G2(t),…,Gl(t)在不变凸集M上依支撑函数可微,下面讨论模糊优化问题(FMP): MinimizeF(t), 设t0∈intM,如果不存在t∈intM,使得F(t)sF(t0),则称t0为模糊优化问题的优化解,F(t0)为目标函数F的优化值. 定理2.4设F(t),G1(t),G2(t),…,Gl(t)是不变凸集M上依支撑函数可微的s-不变凸模糊映射,如果存在 a=(a1,a2,…,al)T∈Rl, 使得: 1) ▽sF(t0)+aT((▽sG1(t0))T,(▽sG2(t0))T,…,(▽sGl(t0))T)T=(0,0,…,0); 4)ai≥0(i=1,2,…,l), 则t0是模糊优化问题(FMP)的优化解. 证明设▽sF(t0)=(u1,u2,…,um),▽sGi(t0)=(ui1,ui2,…,uim)(i=1,2,…,l),且F(t),G1(t),G2(t),…,Gl(t)是s-不变凸的,对任意的t=(t1,t2,…,tm)T∈intM,有 F(t)*(r,x)-F(t0)*(r,x)≥ [▽sF(t0)]η(t,t0)= 对r∈[0,1]和x∈Sn-1一致成立.由于 则根据依支撑函数可微的定义,有 (G1(t)*(r,x)-G1(t0)*(r,x)-o(d(t,t0)), G2(t)*(r,x)-G2(t0)*(r,x)-o(d(t,t0)),…, Gl(t)*(r,x)-Gl(t0)*(r,x)-o(d(t,t0))), 所以 F(t)*(r,x)-F(t0)*(r,x)≥ -aT(G1(t)*(r,x)-G1(t0)*(r,x)-o(d(t,t0)), G2(t)*(r,x)-G2(t0)*(r,x)-o(d(t,t0)),…, Gl(t)*(r,x)-Gl(t0)*(r,x)-o(d(t,t0)))T= -aT(G1(t)*(r,x)+o(d(t,t0)),G2(t)*(r,x)+ o(d(t,t0)),…,Gl(t)*(r,x)+o(d(t,t0)))T= aT(-G1(t)*(r,x),-G2(t)*(r,x),…, -Gl(t)*(r,x))T≥0, 于是t0是模糊优化问题(FMP)的优化解. 致谢陇东学院青年科技创新项目(XYZK1812)对本文给予了资助,谨致谢意.