结构元线性生成的模糊值函数的可导性

舒天军, 莫智文

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

基于扩张原理, 模糊值函数微分是对区间值函数微分的自然推广.但扩展原理中λ遍历区间[0,1],因此模糊值函数的微分在实际应用中的计算变得困难.为了便于模糊值函数微分计算,诸多学者对模糊值函数的可导性进行了探究[1-16].郭嗣琮[17]提出用结构元表示模糊数,简化了模糊数的解析表达式.本文在文献[18-19]介绍的结构元线性生成的模糊数、模糊值函数的基础上,根据文献[20]给出的模糊距离定义一种新的结构元线性生成的模糊值函数的极限,并用这种极限新定义结构元线性生成的模糊值函数的导数,然后结合这种导数的定义研究结构元线性生成的模糊值函数的导数性质.同时，应用结构元线性生成的模糊值函数的导数讨论结构元线性生成的模糊值函数的凸性.

1 预备知识

定义1.1[17]E是实数域R上的模糊集,隶属函数记为E(x),x∈R.如果E(x)满足下述性质：

1)E(0)=1,E(1+0)=E(-1-0)=0;

2) 在区间[-1,0)和(0,1]上,E(x)分别是单调增右连续函数和单调降左连续函数;

3) 在区间(-∞,-1)或(1,+∞)上,E(x)=0,则称模糊集E为R上的模糊结构元.

显然,模糊结构元E是R上的正则凸模糊集,是有界闭模糊集.

定义1.2[18]A是有限模糊数,若存在1个模糊结构元E和有限实数a∈R,r∈R+,使得=a+rE(其中r→0),则称是由模糊结构元E线性生成的模糊数.由E线性生成的模糊数的全体记作

(E)={|=a+rE,∀a∈R,r∈R+},

定义1.3[19]设X、Y是2个实数集,(Y)是Y上的模糊数的全体,是X到(Y)上的映射,即对于任意的x∈X,存在唯一的模糊数(Y)与之对应,记则称为X上的模糊值函数.如果E是N(Y)上1个正则模糊结构元,则称是X上的1个由E线性生成的模糊值函数,其中h(x)、ω(x)在X上有界,且ω(x)>0.由E线性生成的有界模糊函数的全体记作

(Ef)=

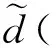
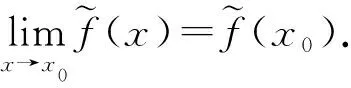
对于任意给的实数ε>0,分别存在δ1与δ2.当x0-x<δ1时,有

当x-x0<δ2时,有

取δ={δ1,δ2},当|x-x0|<δ时,有

则有

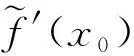
所以对于任给的实数ε>0,存在正数δ,使得0<|x-x0|<δ时,有

成立.于是当x-x0<δ时,有

当x0-x<δ时,有

所以由模糊值函数极限保号性可知,存在正数δ,对一切x1∈(a,a-δ)有

当0<|x-x0|<δ2时,有

令δ=min{δ1,δ2},则当0<|x-x0|<δ时,有

2) 类似于证明1).

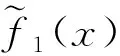
则有

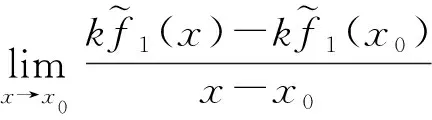
证明作辅助模糊值函数

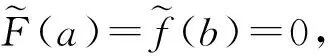
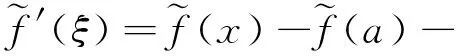
即证明

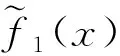
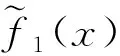
同理可得

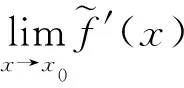
不等式两边取极限可得

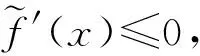
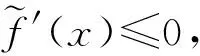
x2=λx1+(1-λ)x3.

从而有

即

成立.

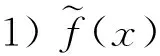
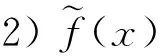
3) 对于I上任意2点x1、x2,有

其中ξ∈(x1,x2).移项后有

当x2

3)→1) 对于I上任意的2点x1、x2,取x3=λx1+(1-λ)x2(其中0<λ<1),有x1-x3=(1-λ)·(x1-x2)与x2-x3=λ(x2-x1).由

可以推出

化简2不等式可得