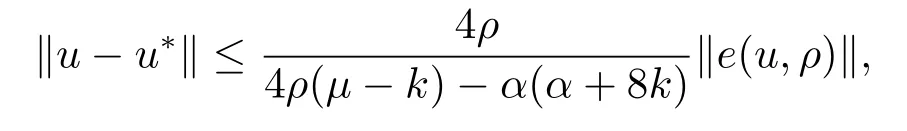EXISTENCE OF SOLUTIONS AND ERROR BOUNDS FOR A GENERALIZED INVERSE MIXED QUASI-VARIATATIONAL INEQUALITY
2019-01-18ZHAOYaliZHANGQianWANGFengjiaoWANGXinghe
ZHAO Ya-li,ZHANG Qian,WANG Feng-jiao,WANG Xing-he
(1.College of Physics and Mathematics,Bohai University,Jinzhou 121013,China)
(2.Department of Economics,University of Missouri-Columbia,Columbia 65211,USA)
Abstract:In this paper,we introduce and study a new class of generalized inverse mixed quasi-variatational inequalities(GIMQVI)in Hilbert spaces.By making use of the properties of generalized f-projection operator,we obtain the existence and uniqueness results for GIMQVI.Moreover,we also establish the error bounds for GIMQVI according to the residual function,which extend and improve some results in the recent literature.
Keywords: generalized inversemixed quasi-variatationalinequality; generalized fprojection operator;error bound;residual function
1 Introduction
It has been realized over the years that variational inequalities and their generalizations provide convenient frameworks for the study and applications of many important issues of nonlinear analysis,partial differential equations,optimization,equilibria,control theory, finance,economics,transportation and the engineering sciences.With the development of variational inequality theory with its applications,several classes of inverse(mixed)(quasi-)variatational inequalities were introduced and studied.In this area,the first work owned to He et al.[1,2]in 2006.They studied a class of inverse variational inequalities and also found their applications in practical world,such as normative flow control problems,which require the network equilibrium state to be in a linearly constrained set,and bipartite market equilibrium problems.Since then,some authors paid more attentions on the inverse variational inequalities and their generalizations.For instance,Yang[3],He and Liu[4],Scrimali[5]studied inverse variational inequalities with their applications.Hu and Fang[6]also studied the well-posedness of inverse variational inequalities.Aussel et al.[7]studied the gap functions and error bounds for inverse quasi-variatational inequality problems.Very recently,Li et al.[8,9]employed generalizedf-projection operator to study algorithm,existence,gap functions and error bounds for inverse mixed(quasi-)variatational inequalities.The concept of the generalizedf-projection operator was introduced by Wu and Huang[10],which is proved to be a good tool to study inverse mixed quasi-variatational inequalities.
Motivated and inspired by the work mentioned above,in this paper,we introduce and study a new class of generalized inverse mixed quasi-variatational inequalities(GIMQVI)in Hilbert spaces.We firstly make use of the properties of generalizedf-projection operator in Hilbert spaces[9,10]to obtain the existence and uniqueness results for GIMQVI.Then we study error bounds for GIMQVI according to the residual function.The results presented here extend and improve the correspond results Theorem 4.1 and Theorems 5.1 and 5.4 in[9].
2 Preliminaries
Throughout the paper,letHbe a real Hilbert space with inner productand norm,letK:H→2Hbe a set-valued mapping such that for eachu∈H,K(u)is a nonempty closed convex subset ofH.LetM,N:H×H→H,A,B,C,D,h:H→Hbe nonlinear single-valued mappings,f:H→R∪{+∞}be proper,convex and lower semicontinuous onK(u)for eachu∈H.We consider the generalized inverse mixed quasi-variatational inequality(GIMQVI)as follows:find au∈H,such thathu∈K(u)and
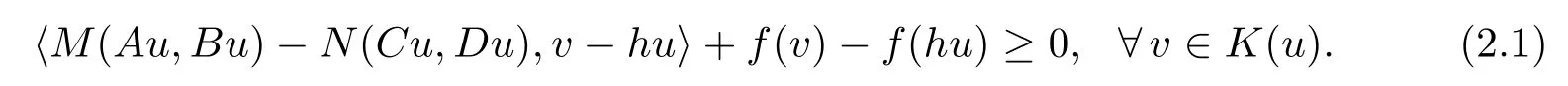
Let us first see some special cases of GIMQVI(2.1).
(1)IfM(u,v)=N(u,v)=ufor allu,v∈H,then GIMQVI(2.1)is reduced to the following inverse mixed quasi-variational inequality:find au∈H,such thathu∈K(u)and
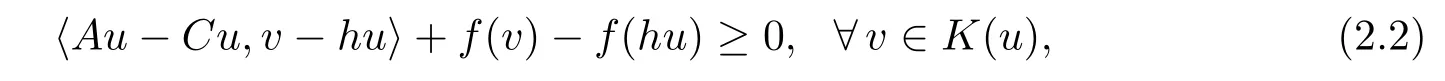
which is to be a new one.
(2)IfBu=Cu=Du=N(u,v)=0,M(u,v)=ufor allu,v∈H,then GIMQVI(2.1)is reduced to the inverse mixed quasi-variational inequality(IMQVI):find au∈Hsuch thathu∈K(u)and
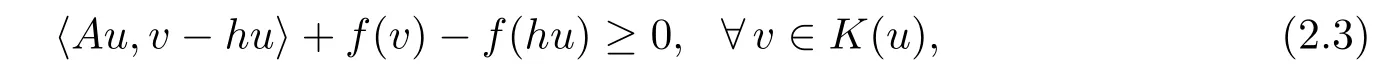
which was introduced and studied by Li and Zou[9].
(3)IfBu=Cu=Du=N(u,v)=0,Au=M(u,v)=u,K(u)=for allu,v∈H,whereis a nonempty closed convex subset ofH,then GIMQVI(2.1)is equivalent to the inverse mixed variational inequality(IMVI)studied by Li,Li and Huang[8]:find au∈Hsuch thatand
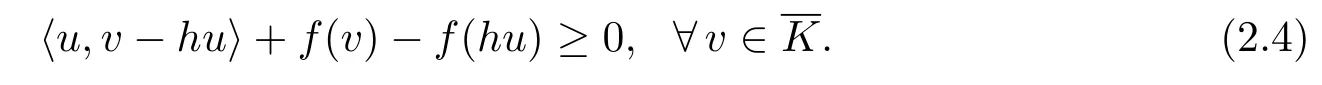
(4)IfH=Rn,f(u)=Bu=Cu=Du=N(u,v)=0,Au=M(u,v)=u,K(u)=for allu,v∈Rn,whereis a nonempty closed convex subset,then GIMQVI(2.1)is reduced to the inverse variational inequality(IVI),first proposed by He and Liu[1]:find au∈Rnsuch thatand
(5)IfH=Rn,f(u)=Bu=Cu=Du=N(u,v)=0,M(u,v)=ufor allu,v∈Rn,then GIMQVI(2.1)reduces to the inverse quasi-variational inequality(IQVI)introduced and studied by Aussel et al.[7]:find au∈Rnsuch thathu∈K(u)and

Moreover,ifAis the identify mapping onRn,then IQVI(2.6)reduces to the following inverse quasi-variational inequality:find au∈Rnsuch thathu∈K(u)and
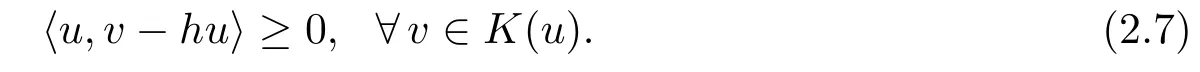
(6)IfH=Rn,f(u)=Bu=Cu=Du=N(u,v)=0,M(u,v)=hu=ufor allu,v∈Rn,then GIMQVI(2.1)becomes the classic quasi-variational inequality(QVI):find au∈K(u)such that

QVI was introduced and investigated at first by Bensoussan and Lions[11,12].They introduced these problems in connection with impulse optimal control problems.
In a word,GIMQVI(2.1)is more general,which concludes many new and known inverse mixed(quasi-)variational inequalities,inverse(quasi-)variational inequalities,mixed(quasi-)variational inequalities and(quasi-)variational inequalities as its special cases.
In order to obtain our main results,we need the following definitions and lemmas.Now,we first recall the concept and properties of the generalizedf-projection operator,which play an important role in obtaining our main results.
LetG:H×K→R∪{+∞}be a functional defined as follows:
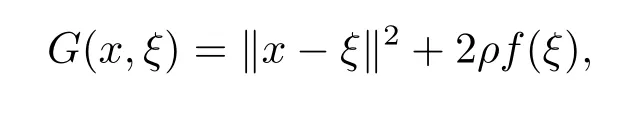
whereξ∈K,x∈H,ρis a positive number andf:K→R∪{+∞}is a proper,convex,and lower semicontinuous function.
Definition 2.1[10]LetHbe a real Hilbert space,andKbe a nonempty closed and convex subset ofH.We call thatis a generalizedf-projection operator if

From the work of Wu and Huang[10]and Fan et al.[13],we know that the generalizedf-projection operator has the following properties.
Lemma 2.2[10,13]LetHbe a real Hilbert space,andKbe a nonempty closed and convex subset ofH.Then the following statements hold
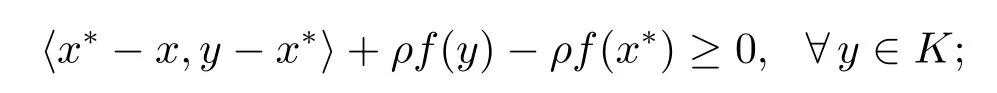
In addition,letK:H→2Hbe a set-valued mapping such that for eachx∈H,K(x)is a closed convex set inH.Similarly,we can define the generalizedf-projection of anyz∈Hon the setK(x),that is,
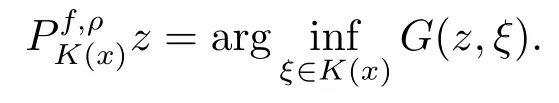
In 2016,Li and Zou applied the basic inequality in Lemma 2.2 to prove the properties(for details,see Theorems 3.1 and 3.3 in[9])of the operatorin Hilbert spaces.
Definition 2.3[10,13]LetHbe a real Hilbert space,andN:H×H→H,A,B,g:H→Hbe four single-valued mappings.
(i)gis said to beα-Lipschitz continuous onH,if there exists a constantα>0 such that

(ii)Nis said to beβ-g-strongly mixed monotone with respect toAandBif there exists a constantβ>0 such that
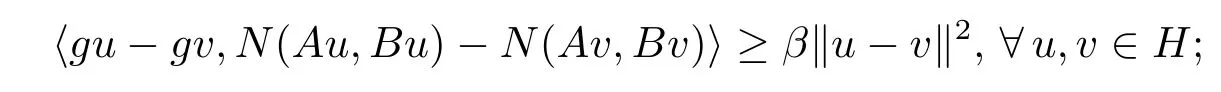
(iii)Nis said to beγ-strongly mixed monotone with respect toAandBif there exists a constantγ>0 such that
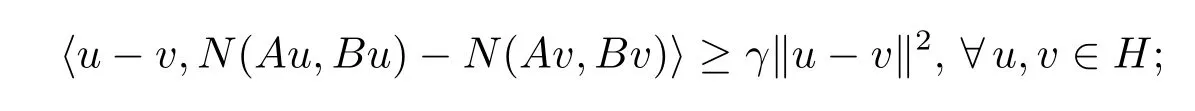
(iv)Nis said to beδ-Lipschitz continuous with respect toAandBif there exists a constantδ>0 such that
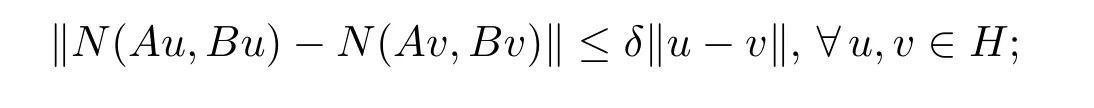
(v)Nis said to beυ-g-relaxed Lipschitz with respect toAandBif there exists a constantυ>0 such that
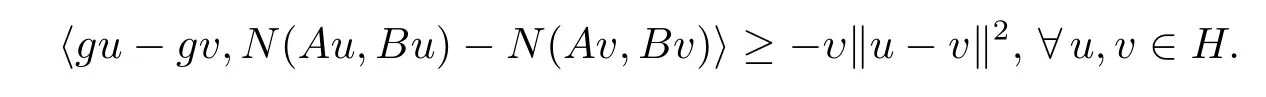
Remark 2.4Note that ifg≡I,identify mapping onH,theng-strong mixed monotonicity ofNwith respect toAandBreduces to the strong mixed monotonicity ofNwith respect toAandB.Moreover,ifN(Au,Bu)=Aufor allu∈H,theng-strong mixed monotonicity ofNwith respect toAandBreduces to the ordinaryg-strong monotonicity ofAand strong mixed monotonicity ofNwith respect toAandBreduces to the general strong monotonicity ofA.
3 The Existence and Uniqueness Results of GIMQVI
In this section,we give the existence and uniqueness results of GIMQVI(2.1)by the properties of generalizedf-projection operator under certain conditions.
From the properties of generalizedf-projection operator thatu∈His a solution of GIMQVI(2.1)if and only ifusatisfies

whereρ>0 is a constant.
Theorem 3.1LetHbe a real Hilbert space,andK:H→2Hbe a set-valued mapping such that for eachu∈H,K(u)⊂His a closed convex set andf:H→R∪{+∞}be proper,convex and lower semicontinuous onK(u).LetM,N:H×H→H,A,B,C,D,h:H→Hbe nonlinear single-valued mappings.If the following conditions hold
(i)hisα-Lipschitz continuous;
(ii)Misβ-Lipschitz continuous with respect toAandBandNisγ-Lipschitz continuous with respect toCandD;
(iii)Misλ-strongly mixed monotone with respect toAandB;
(iv)Misµ-h-strongly mixed monotone with respect toAandB;
(v)there existsk>0 such that

ProofLetF:H→Hbe defined as follows
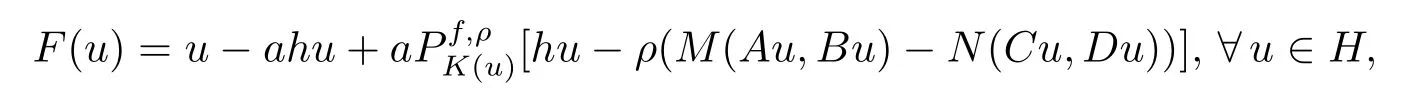
wherea>0 is a constant.For anyu,v∈H,we have
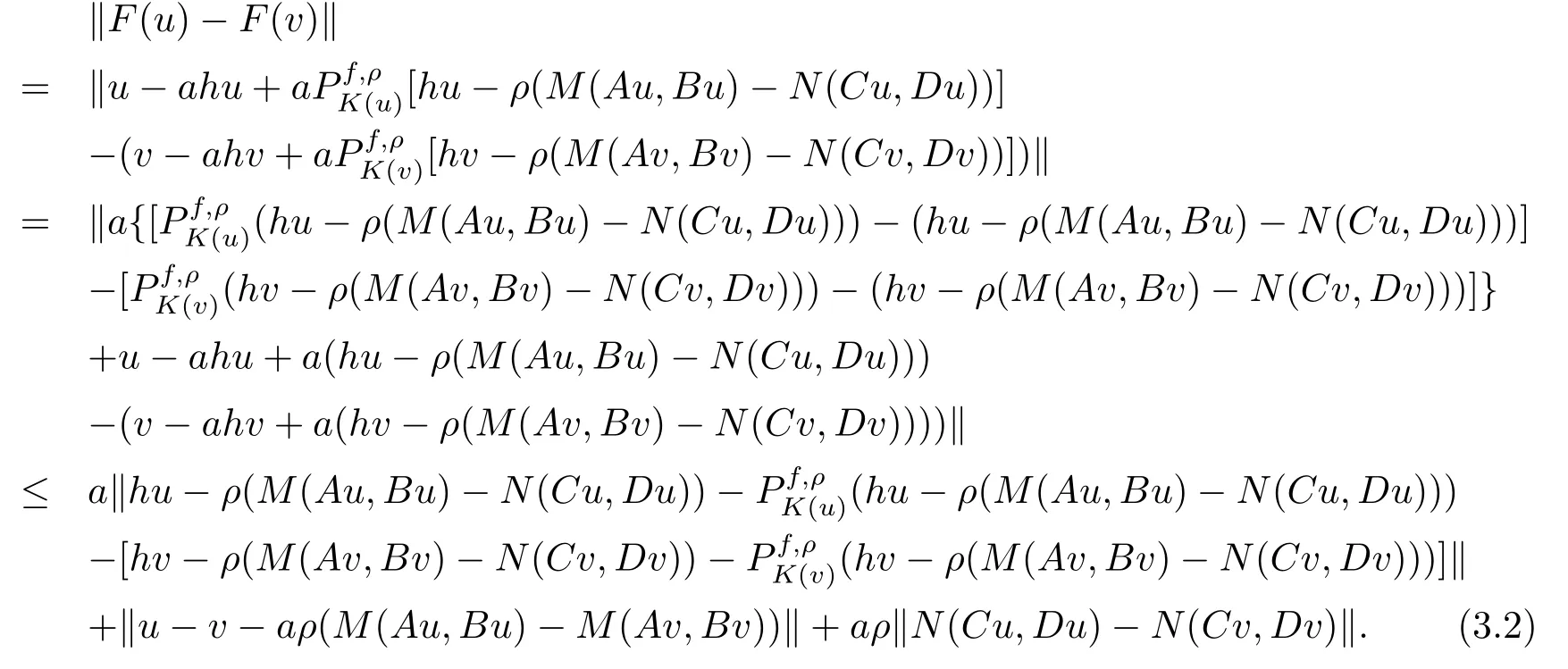
It follows from condition(v)and Theorem 3.3 of[9]that

By conditions(i),(ii),(iv),we get
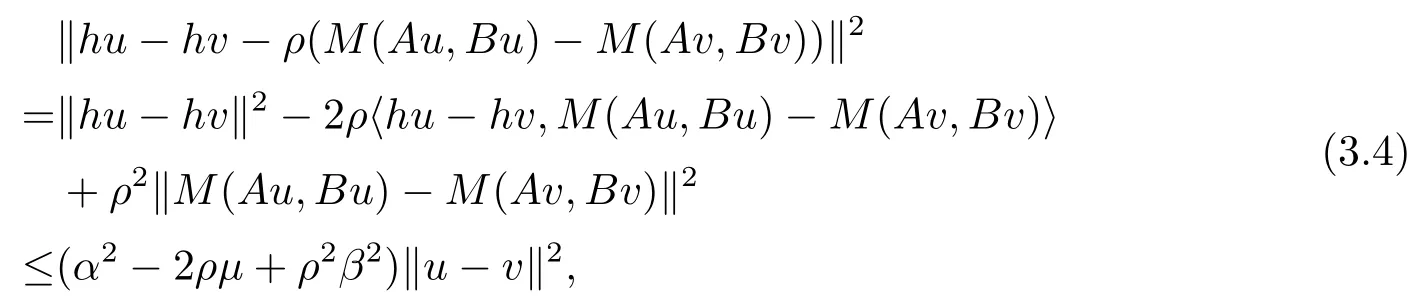
and by conditions(ii)and(iii),we have
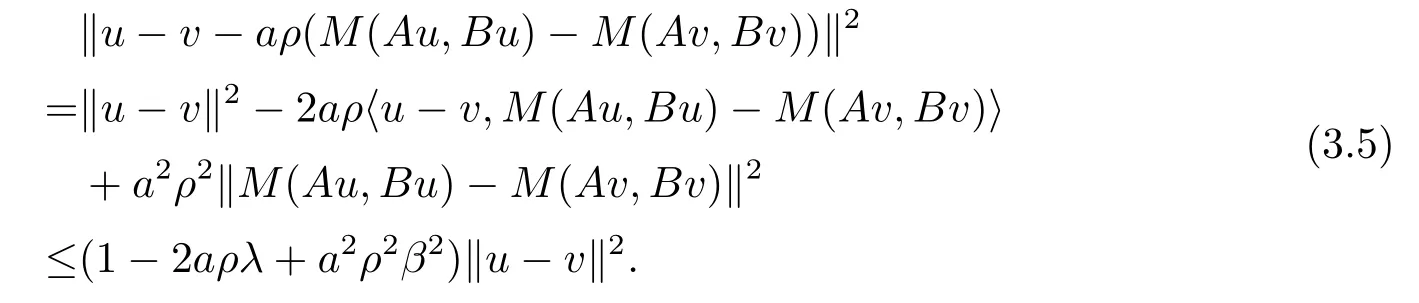
It follows from(3.2)–(3.5)and condition(iv),we have
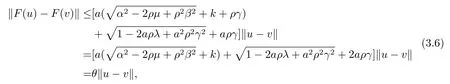
where.It follows from condition(vi)thatθ<1,thereforeFis a contracting mapping in Hilbert spaceH.So,Fhas a uniquefixed pointu∗∈H,that isF(u∗)=u∗,implying thatu∗∈K(u∗)and

thusu∗is a unique solution of GIMQVI(2.1).This completes the proof.
Corollary 3.2LetH,K,fbe same as in Theorem 3.1.h,A:H→Hbe Lipschitz continuous with Lipschitz constantsαandβ,respectively.Assume that
(i)Aisλ-strongly monotone andAisµ-h-strongly monotone onH;
(ii)there existsk>0 such that
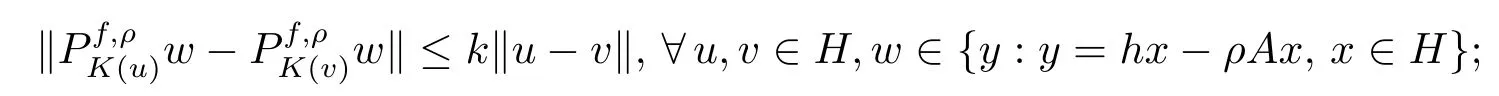
Then IMQVI(2.3)has a unique solution inH.
Remark 3.3Theorem 3.1 extends Theorem 4.1 of[9].
4 Error Bounds for GIMQVI
It is well known that error bounds are closely related to the rate of convergence of algorithms,which play important roles in the study of variational inequality and optimization problems.They allow us to estimate the distance from a feasible element to the solution set even without having computed a single solution of the related variational inequality and optimization problems.In this section,we give two main error bound results for GIMQVI(2.1)by different methods.
By(3.1),let
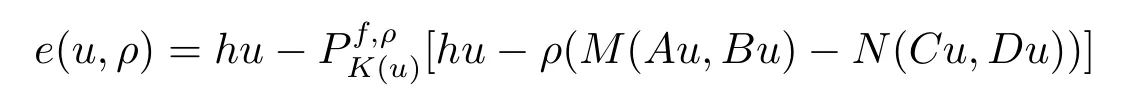
denote the residual function.Observe that GIMQVI(2.1)has a solutionūif and only ifūis a zero point ofe(u,ρ).Now we give the error bounds according to the residual functione(u,ρ).
Theorem 4.1LetH,K,M,N,A,B,C,D,hbe same as in Theorem 3.1 and satisfy conditions(i)–(iv)in Theorem 3.1.If the following conditions hold
(a)Nisυ-h-relaxed Lipschitz with respect toAandB;
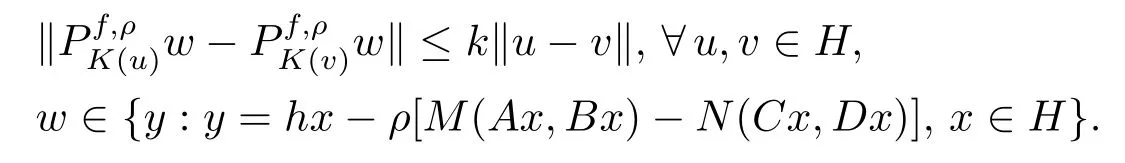
Ifu∗is the solution of GIMQVI(2.1),then for anyu∈Hand,we have
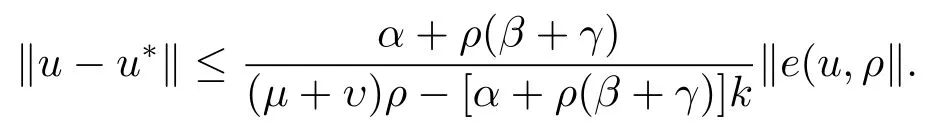
ProofLet.Sinceu∗is the solution of GIMQVI(2.1),then,for allρ>0,we have
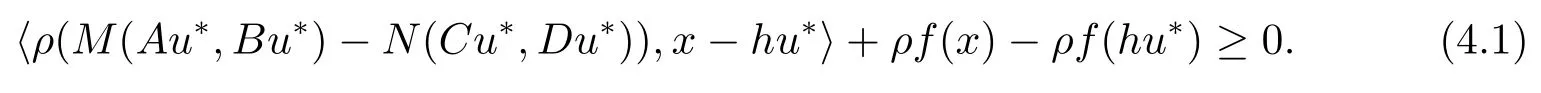
From the definition ofxandhu∗∈K(u∗),we have
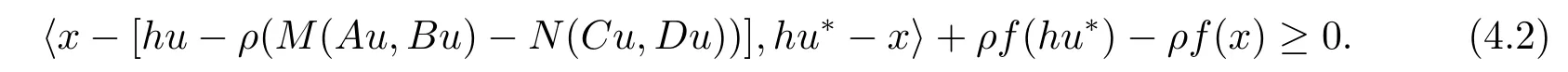
It follows from(4.1)and(4.2)that
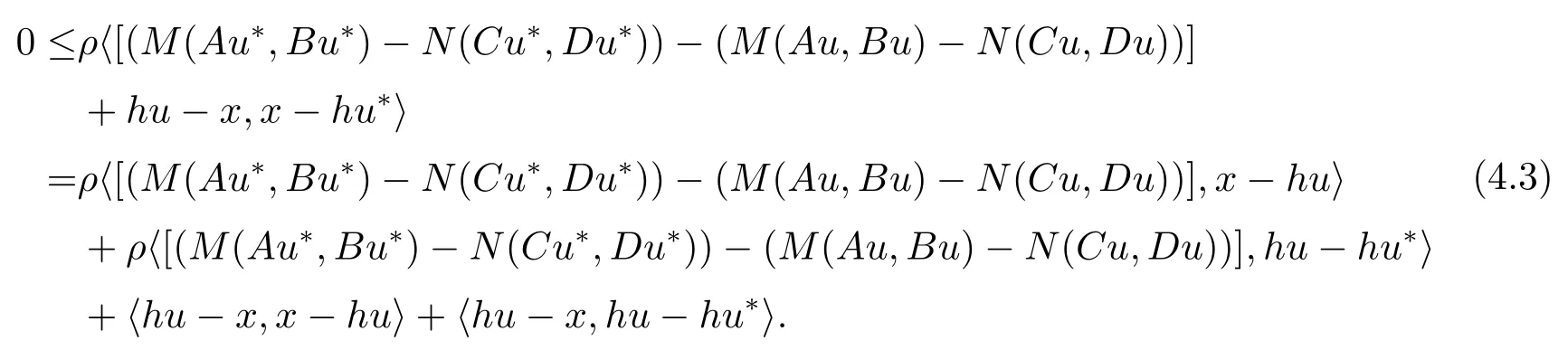
By condition(iv)in Theorem 3.1 and condition(a),we get
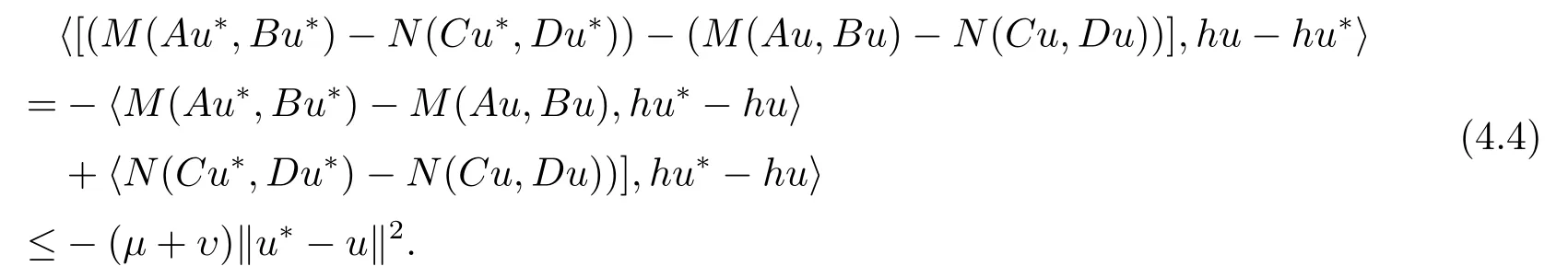
By conditions(i)and(ii)in Theorem 3.1,(4.3)and(4.4),for any,we obtain that
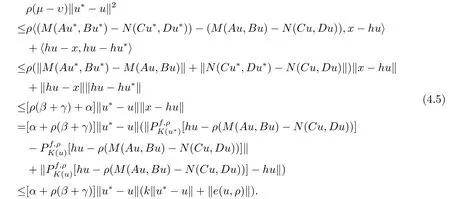

which is completes the proof.
IfM(Au,Bu)=Au,N=0 for allu∈H,from Theorem 4.1,we obtain the following result.
Corollary 4.2LetH,K,f,hbe same as in Theorem 4.1.Assume that
(a1)Aisβ-Lipschitz continuous andAisµ-h-strongly monotone;
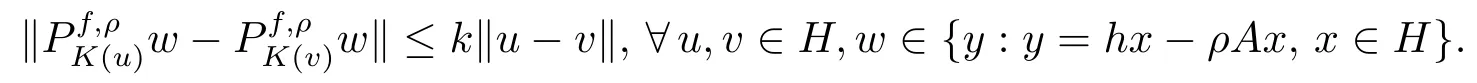
Ifu∗is the solution of IMQVI(2.3),then for anyu∈Hand,we have
IfH=Rn,M(Au,Bu)=Au,N=0 andf(u)=0 for allu∈Rn,then Theorem 4.1 reduces to the following.
Corollary 4.3Leth,A:Rn→Rnbe Lipschitz continuous with Lipschitz constantsαandβ,respectively.LetK:Rn→2Rnbe set-valued mapping such that for eachu∈Rn,K(u)⊂Rnis a nonempty closed convex set.Assume that
(a2)Aisµ-h-strongly monotone;
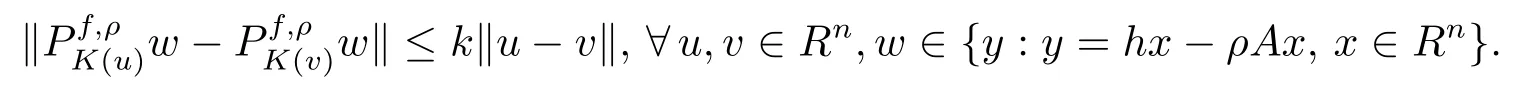
Ifu∗is the solution of(2.6),then for anyu∈Rnand,we have

wheree(u,ρ)=hu−PK(u)[hu−ρAu],PK(·)wis the general projection ofwonto the nonempty closed convex subsetK(·)ofRn.
Remark 4.4Theorem 4.1 extends Theorems 5.1 and 5.2 in[9].Applying this property of,we prove another error bound result for GIMQVI(2.1).
For anyu∈H,by Theorme 3.3 of[9],we know thatis a firmly expansive onH.
Theorem 4.5LetH,K,M,N,A,B,C,D,hbe same as in Theorem 3.1 and satisfy conditions(i)–(iv)in Theorem 3.1 and condition(a)in Theorem 4.1.If the following condition holds
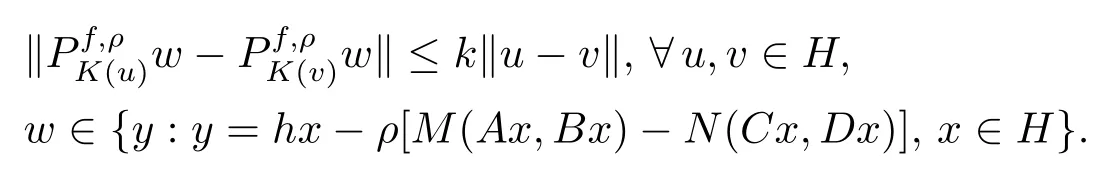
Ifu∗is the solution of GIMQVI(2.1),then for anyu∈Hand,we have
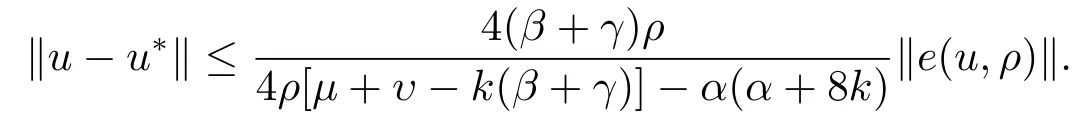
ProofLet
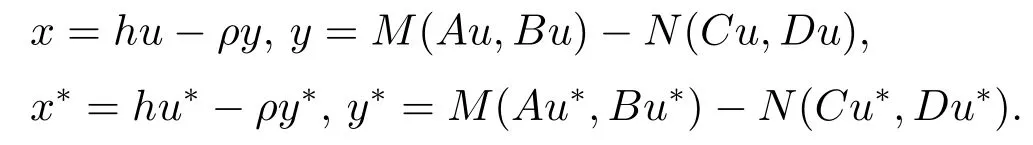
From the definition ofe(u,ρ),we have

By conditions(i),(ii),(iv)in Theorem 3.1 and condition(a)in Theorem 4.1,it follows from(4.6)and Theorem 3.1 of[9]that

On the other hand,by condition(ii)in Theorem 3.1 again,we have


This completes the proof.
IfM(Au,Bu)=Au,N=0 for allu∈H,from Theorem 4.5,we have the following corollary.
Corollary 4.6LetH,K,f,hbe the same as in Corollary 4.2 and satisfy condition(a1)in Corollary 4.2.Assume that


IfH=Rn,M(Au,Bu)=Au,N=0 andf(u)=0 for allu∈Rn,his an identity mapping onRn,then Theorem 4.5 reduces to the following result.
Corollary 4.7LetH,K,Abe the same as in Corollary 4.3.Assume that
(a3)hisµ-strongly monotone onRn;
(b5)there exists 0 Ifu∗is the solution of(IQVI)(2.6),then for anyu∈Rnand any,we have wheree(u,ρ)=hu−PK(u)(hu−ρu),PK(·)wis the general projection ofwonto the nonempty closed convex subsetK(·)ofRn. Remark 4.8Theorem 4.2 extends Theorems 5.3 and 5.4 in[9].