基于两种SPEI序列的淮河流域干湿特征变化

冯 怡，薛联青，张 敏，苗智英，任 磊，张子沐

(1．河海大学水文水资源学院，江苏南京 210098;2．江苏省洪泽湖管理委员会办公室，江苏淮安 223100;3．河海大学农业工程学院，江苏南京 210098)

受气候变化和人类活动的影响，全球水分循环给地区的干湿状况带来了不可忽视的变化，继而对地区的社会经济发展产生了重大影响，因此，区域性的气候干湿状况受到广泛关注。干旱指数是监测、预警、评估干旱的关键参数，可标记干湿发生时间和强度，反映干湿发生机理[1]。目前标准化降水指数(standardized precipitation index，SPI)是国内外用于干湿状况监测最常用的指标之一[2]。假定所有地点旱涝发生概率相等，SPI以降水为基础进行区域的干湿变化评价，但无法标识旱涝频发地区，且未考虑以蒸发为主的水分支出。在全球变暖的背景下，气温升高对水量平衡的影响不容忽视。Vicente-Serrano等[3]提出的标准化降水蒸散指数(standardized precipitation evapotranspiration index，SPEI) 考虑了蒸散发的水分支出作用，符合自然界的水量平衡关系;对比帕默尔干旱指数(Palmer drought severity index，PDSI)，SPEI计算简便，可评估不同时间尺度的干湿程度。凭借概率计算的特点和空间可比性等优点，SPEI目前已成为干湿特征分析新的理想指标。近年来，国内外已有众多学者采用SPEI对区域干湿状况进行计算和分析。Zhu等[4]采用不同时间尺度的SPI和SPEI进行了水文干旱监测的对比分析;Vicente-Serrano等[5]基于SPEI分析了大气环流指数对欧洲干旱状况的影响程度;陈子燊等[6]计算了多时间尺度的SPEI，采用REOF、Mann-Kendall趋势检验和小波分析等方法分析了广东1962—2007年的干湿时空变化特征;刘珂等[7]利用两种潜在蒸散发算法的SPEI对全国的干湿变化特征进行了分析。目前基于SPEI的干湿变化研究主要从流域的时空变化分析展开，而在整体干湿变化的基础上，不同气象要素对流域干湿变化影响的研究相对较少。

为研究不同气象要素对流域干湿变化的影响程度，深入探究流域的时空干湿变化特征，本文采用基于多种气象要素的FAO56 Penman-Monteith法(P-M法)[8]和仅考虑温度的Hargreaves-Samani法(Har法)[9]两种潜在蒸散发的计算方法，基于12个月尺度的SPEI对洪泽湖以上淮河流域进行年尺度的干湿变化研究，定量分析两种SPEI序列对不同气象要素的敏感性，以期为SPEI在江淮地区及全国干湿变化研究中的应用提供参考。

1 研究区域概况

淮河流域降水时空分布不均，有些年份夏秋连旱，洪涝和旱灾频发，是典型的“孕灾”区域。选取洪泽湖以上的淮河中上游为研究区域，该区域水系呈典型的扇状分布，汇水面积达15．8万 km2[10-11]。作为整个淮河流域的主要产流区，淮河中上游也是洪泽湖入湖水量的主要来源[10]。该区域介于长江流域和黄河流域之间，是北亚热带向暖温带过渡区，属大陆性季风气候。降水受夏季风影响，主要出现在汛期(5—9月)，年降水量多为600～1400 mm。选取淮河中上游20个气象站点1960—2016年的降水P、平均温度T、最高温度Tmax、最低温度Tmin、日照时数Sd、平均风速W和相对湿度Rh等日尺度数据，基于两种潜在蒸散发计算方法的SPEI序列进行流域干湿时空变化分析和敏感性分析。相关数据来源于中国气象数据共享网(http：//data．cma．cn/)。 图1是包含了20个气象站点的洪泽湖以上淮河中上游流域图。

图1 洪泽湖以上淮河中上游流域及气象站点分布

2 研究方法

2.1 SPEI计算方法

SPEI是对降水量与潜在蒸散发的差值序列累积概率值进行正态标准化后的一种指数。本文采用P-M法和Har法分别计算月潜在蒸散发，然后计算逐月降水与蒸散发的差值，建立不同时间尺度的累积序列，采用Log-logistic分布对数据序列进行拟合及标准化转换，得到不同时间尺度的SPEI。以12个月时间尺度的SPEI表征研究区域的气象干湿状况，采用算术平均法求得流域平均SPEI。根据中国气象局制定的SPEI干湿等级划分标准(表1)对流域干湿等级进行划分。

表1 SPEI的干湿等级划分及概率

2.2 潜在蒸散发计算方法

Hargreaves和Samani在1985年推导出基于温差的作物潜在蒸散发计算公式(Hargreaves-Samani公式，式(1))，基于该公式的Har法在缺少气象资料的地区广泛应用，并被证明是一个有效的估算方法，估算时需要温度(平均、最高、最低)和地理位置数据。

式中：Eh为基于Har法的潜在蒸散发;T为平均温度，℃;Tmin为最低温度，℃;Tmax为最高温度，℃;Ra为大气顶太阳辐射，MJ/(m2·d);λ是水汽化潜热，MJ/kg。

Penman法是依据能量平衡和紊流扩散原理推导出的计算参考作物蒸散发的方法，具有坚实的理论基础。经历了漫长的发展历程，在Penman法的基础上，包含了风函数的P-M法成为目前使用最多的潜在蒸散发计算方法，其计算公式为

式中：Epm为基于P-M法的潜在蒸散发;Δ为温度饱和水汽压关系曲线T处斜率，kPa/℃;es为饱和水汽压，kPa;ea为实际水汽压，kPa;u2为2 m高处风速，m/s;Rn为净辐射，MJ/(m2·d);G为土壤热通量，MJ/(m2·d);γ为湿度计常数，kPa/℃;各参数具体公式参见文献[12]。基于Har法和P-M法计算所得的干旱指数记为SPEIh、SPEIpm。

2.3 去趋势方法

为了定量研究两种潜在蒸散发计算方法所得SPEI序列对不同气象要素的敏感性，采用单一气象要素不变、其他气象要素去趋势的去趋势方法[13-14]，结合两种潜在蒸散发计算方法得到新的潜在蒸散发序列，对不同的SPEI序列进行分析研究。所有气象要素去趋势情况简称为去趋势，实测数据未去趋势情况简称为未去趋势，只保留一种气象要素趋势的情况则为部分去趋势。所有的SPEI和气象要素序列均采用非参数Mann-Kendall检验法的Sen’s斜率进行趋势计算[15]。简单去趋势方法用于消除站点原始气象要素的线性趋势，可直接应用于空气温度参数，但对于其他有范围限制的气象要素例如相对湿度(0＜Rh＜1)、风速和日照时数(W＞0，Sd＞0)，先采用简单去趋势方法，然后结合参数的区间限制条件进行相关处理以避免不合理的结果。温度的去趋势公式为

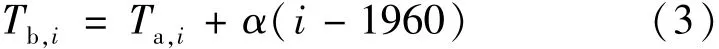
式中：Tb，i为温度 T 在年份 i的去趋势值;Ta，i为相同年份的最初温度;α为所选站点的温度趋势值;i代表年份(1960—2016年)。

对于其余气象要素，受本身的范围区间影响，需要对去趋势方法进行改进，改进公式为

式中：Fb，i为年尺度下气象要素的去趋势值;Fa，i为年尺度下气象要素的实际值;Fb，i′为日尺度下气象要素的去趋势值;Fa，i′为日尺度下气象要素的实际值;α为实际气象要素曲线的变化斜率。

3 结果与讨论

3.1 两种SPEI与潜在蒸散发序列的时间对比

图2是1960—2016年淮河流域两种SPEI序列和潜在蒸散发序列对比图。从图2(a)可知，流域的平均温度距平为显著上升趋势，流域呈增温现象。两种SPEI序列差异较小，线形基本吻合，流域整体呈现变湿趋势，SPEI值主要在-2～2之间波动，根据表1的干湿等级，流域干湿等级主要在中等干旱和中等湿润之间相互转换。两种SPEI序列与温度距平的线形走势相反，温度距平越大，SPEI越小，温度距平越小，SPEI越大，二者呈负相关关系。SPEIpm的整体斜率为 0．0085，SPEIh的整体斜率为0．0049，略低于前者，研究区呈现变湿趋势，温度距平曲线的斜率为0．02，明显大于SPEI曲线的斜率，说明流域温度变化较干湿变化更明显。SPEI除受温度影响外，还受降水等其他气象因素的影响，因此研究区的干湿变化程度小于温度的变化程度。

图2 1960—2016年淮河流域干湿变化和蒸散发变化

不同于SPEI序列的高吻合度，潜在蒸散发整体呈下降趋势(图2(b))，与温度距平的上升趋势形成强烈对比，潜在蒸散发距平随温度距平的变化而变化，二者为显著负相关关系。Epm的斜率为-1．72， Eh的斜率为 -0．78，前者的下降速率约为后者的2倍，从图2(b)可以看出，Epm距平随温度距平变化较Eh更强烈，说明Epm对温度的升高更敏感。潜在蒸散发距平越大，两种潜在蒸散发距平的差值越大，例如1966年和2004年。对照图2(a)可知，潜在蒸散发距平越大，SPEI值反而越小，流域呈现干旱状态;反之，潜在蒸散发距平越小，SPEI值越大，流域呈现湿润状态。

3.2 两种SPEI序列的空间分布特征

采用非参数Mann-Kendall检验法对两种SPEI序列曲线进行斜率计算，分析流域的干湿空间变化情况。图3为1960—2016年SPEI序列曲线的斜率空间分布，对比图3(a)和(b)，流域西北地区(河南境内)的SPEIpm曲线斜率大于0，说明该地区呈现变湿趋势;而SPEIh曲线的斜率分布显示，流域西北大部分地区和洪泽湖周边区域均有变湿趋势，河南西华站周边地区的SPEIh曲线斜率小于0，与SPEIpm的分布结果不同。图3(c)(d)为去趋势后的SPEI斜率分布，对比图3(a)(b)，去趋势后的SPEI曲线斜率明显减小，说明气象要素去趋势对SPEI的斜率有显著影响，但流域干湿变化区域不变，说明去趋势过程不改变SPEI在流域各地区的变化趋势，仅影响SPEI值的趋势变化幅度。对比图3(a)和(c)，SPEIpm去趋势后，曲线斜率大于0的区域增加，增大的范围主要分布于流域的东部和南部地区，SPEIh的变化趋势的分布地区基本不变。去趋势后的SPEIpm曲线斜率变化幅度较SPEIh更大，其变化范围从-0．0029 ～0．0242 变为 -0．0108 ～0．0067，说明去趋势过程对SPEIpm影响更大。整个研究区域的SPEI曲线斜率变化相对较小，斜率绝对值不大于0．05，说明流域未来的干湿情况不会发生显著变化，干湿状况相对稳定。

图3 SPEI序列曲线的斜率空间分布

3.3 SPEI对不同气象因素的敏感性

图4 为去趋势、未去趋势及部分去趋势等多种情况的两种SPEI序列频数分布(图中Rh为只保留相对湿度趋势的情况，Sd为只保留日照时数趋势的情况，T为只保留温度趋势的情况，W为只保留风速趋势的情况)，降水去趋势后对SPEI没有影响，因此不加以讨论。Har法只涉及温度，因此SPEIh只有未去趋势、去趋势和只保留温度趋势3种结果的对比。

从图4(a)可以看出，未去趋势情况下，两种SPEI序列的概率密度函数曲线大致相同，二者在SPEI为-1～1的频数相差较大，SPEIpm的洪旱正常等级的概率大于SPEIh。而去趋势后的结果与未去趋势不同，SPEIh比SPEIpm在-1～1的频数更多(图4(b))，说明SPEIh结果显示的流域正常及轻度洪旱等级的频率高于SPEIpm。因此，去趋势前SPEIpm显示的洪旱正常概率高于SPEIh，去趋势后结果相反。从图4(c)概率密度函数曲线的吻合度可以看出，仅SPEIh去趋势情况的洪旱正常频数大于另3种情况，其余3种情况的概率密度函数曲线基本重合，但频数分布直方图相差较大，SPEIpm去趋势后，其处于0．5～1的频数大于另外两种情况，说明此种情况下的轻度干旱有所增加。只保留日照时数趋势和去趋势的对比结果显示(图4(c))，后者的正常洪旱概率略高于前者。由图4(c)可知，只保留相对湿度趋势的SPEIpm在-1～1的频数明显低于去趋势的SPEIpm，只保留风速趋势的SPEIpm在-1～1的频数分布更多，流域将出现更多正常和轻度洪旱现象。

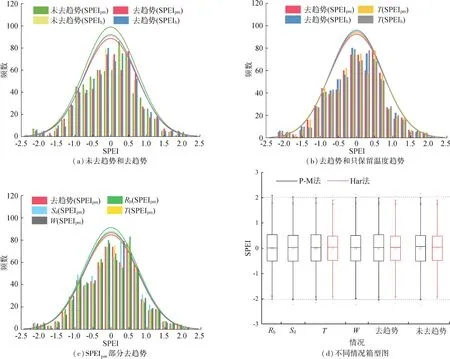
图4 两种SPEI序列对多种气象要素的敏感性分析

从图4(d)的对比可知，多种情况下SPEI值的上下边界值、中位数变化不明显。未去趋势情况下，两种序列SPEI的上下界相近，SPEIpm的中位数和平均值略高于SPEIh。与去趋势情况对比，未去趋势SPEIpm的中位数和平均值有小幅度的提高，说明去趋势后SPEI值整体偏大，但偏大幅度不明显。整体来看，多种情况的上下边界范围在-2～2，平均值和中位数保持在零左右，说明流域的平均旱涝水平在中等干旱和中等洪涝之间，没有极端的旱涝事件发生，整体干湿状况保持稳定。

表2是以上多种情况概率密度函数的μ值和σ值。可以看出，P-M法下，只保留温度趋势情况下SPEIpm的μ值减小了0．145%，流域的干旱趋势增强，另3种去趋势情况下，μ值分别增加了0．000 7%、0．138%和0．121%，说明概率密度函数向右侧偏移，流域有变湿趋势，其中后两种情况的趋势变化更明显。Har法下，只保留温度趋势情况下流域的干旱趋势增加，但 SPEIh的 μ值只减小0．034%，对流域干湿变化影响不明显。除只保留相对湿度趋势的情况外，其余多种情况的σ值较去趋势情况均有所增加，流域的正常及轻度旱涝等级概率增加。

表2 多种情况下SPEIpm和SPEIh的变化对比 %

结合图4(a)(b)(c)可知，温度、日照时数和风速为流域旱涝变化的主要因素。温度升高增加干旱概率，减小淮河流域轻度旱涝及以上等级的概率。相对湿度、日照时数和风速的变化趋势是造成流域向湿润发展的气象因素，日照时数和风速的趋势可增加正常及轻度洪旱等级的概率，减小更高等级的洪旱事件出现的概率，而相对湿度的趋势则会增加流域轻度以上的洪旱概率，不利于地区的发展。综上可得，对淮河流域干湿变化影响程度从大到小的因素分别是温度、日照时数、风速、相对湿度。

4 结 论

a.两种SPEI序列均显示淮河中上游存在变湿趋势;SPEI和温度距平呈负相关关系，潜在蒸散发与温度呈正相关关系。潜在蒸散发距平值越大，SPEI值越小，流域为变干趋势;反之，潜在蒸散发距平值越小，SPEI值越大，流域为变湿趋势。流域西北呈变湿趋势、东部洪泽湖地区的干湿变化趋势是两种SPEI序列曲线斜率分布图的差异所在;去趋势过程不改变SPEI的趋势变化分布，但影响流域的干湿变化强度。整个流域的SPEI曲线斜率变化较小，说明流域未来的干湿情况不发生显著改变。

b.淮河中上游流域干湿变化影响因素由强到弱顺序依次为温度、日照时数、风速和相对湿度。4种气象要素的趋势变化可影响流域干湿等级的概率分布情况;温度的升高增加流域的干旱趋势，日照时数、相对湿度和风速是造成流域湿润的气象因素。