基于松鼠腿部特性的跳跃机理研究与仿生设计*

王永健，冯宝林，殷 磊

(1.中国科学技术大学，安徽 合肥 230026； 2.中国科学院合肥物质科学研究院，安徽 合肥 230031)

0 引 言

在机器人的运动过程中，当障碍物的尺寸显著大于机器人的自身尺寸时，目前地面移动机器人的诸多运动形式会由于地形障碍而失效。而跳跃机器人得益于其自身的运动特点，能够轻松越过数倍于自身尺寸的障碍物，具有超强的越障能力，是解决上述问题的有效方法，在星际探测、军事侦察及灾难搜索等领域具有广阔的应用前景[1-2]，同时由于其运动灵活，移动速度快等特点，跳跃机器人正逐渐成为机器人领域新的研究热点。

国内外的学者对于跳跃机器人已经做了大量的研究。1984年MIT的研究人员设计出了一种单腿跳跃机器人[3]，该机器人类似一个带弹簧的倒立摆，此后的单腿跳跃机器人大多采用与此类似的结构。瑞士洛桑联邦理工大学开发的蚱蜢仿生跳跃机器人采用并联弹性驱动设计，该机器人的垂直跳跃高达1.3 m，每4 s可完成一次跳跃[4]；加州大学伯克利分校的 Haldane D等人利用平面八杆机构模仿夜猴腿部的变机械增益机构，研制出平均每隔0.58 s就可以进行一次高达 1 m跳跃的Salto 机器人[5-6]。哈尔滨工业大学的王猛设计了仿青蛙跳跃机器人，其后肢采用五杆机构作为腿部主体，大腿位置的机构中并联直线弹簧，该机构与青蛙跳跃有相似的力学规律[7]。西北工业大学的葛文杰等人设计了一种基于齿轮—六杆变胞机构的仿袋鼠跳跃机器人，该机器人的腿部并联有直线弹簧。通过改变齿轮-六杆变胞机构的拓扑结构，该机器人具有储能、能量锁定与释放、改变储能大小的功能，因此具有跳跃轨迹的可控性[8]。

笔者以我国常见的灰松鼠[9]为研究对象，对其生物结构和运动机理进行分析并建立其跳跃运动模型，在此基础上进行运动学和动力学分析。最后模仿灰松鼠的腿部结构，仿生设计出一种柔性跳跃机构，并对其进行仿真分析。

1 松鼠跳跃机理及实验观测

选择健康活跃的成年灰松鼠进行生物特性实验，解剖并分析其后腿的结构特征和生理特征，包括骨骼结构、肌肉肌腱的分布、关节驱动等。通过高速摄像系统拍摄并记录灰松鼠起跳过程中各关节转角的变化情况，对其起跳阶段的腿部运动学特性进行分析，解析其运动学特性和肌肉骨骼等的关联，为仿生机构设计提供生物学支撑。

1.1 腿部结构和运动机理

和大多数跳跃动物类似，松鼠主要依靠其后腿快速蹬地提供跳跃的主要动力，从而获得所需的起跳速度。松鼠后腿主要包括大腿，小腿和柔性脚等部分，其中，大腿包括大腿骨和附着其上的股肌，小腿包括胫腓骨和与其近似平行的双关节腓肠肌，柔性脚包括跗骨和多节趾骨。各段骨骼之间通过关节连接，肌肉通过肌腱拉动骨骼绕关节转动。松鼠后腿的结构如图1所示。

灰松鼠的跳跃能量主要由股肌收缩提供，股肌及其弹性肌腱组织共同构成了串联弹性驱动器，牵引胫腓骨绕膝关节旋转。灰松鼠腿部的髋关节、膝关节、踝关节及趾关节各有一个转动自由度，在起跳过程中，灰松鼠的双关节腓肠肌在跳跃过程中只做等长收缩，不能克服阻力做机械功，可视为弹性连杆。 考虑松鼠的跳跃运动基本上是在竖直平面内完成，且在起跳阶段，两只后腿同步协同运动，趾尖始终与地面接触，且脚趾绕趾尖转动，所以将松鼠的跳跃模型简化为单足平面运动，根据松鼠腿部各部分的结构和运动特征，抽象并建立松鼠跳跃的生物运动模型，如图2所示。

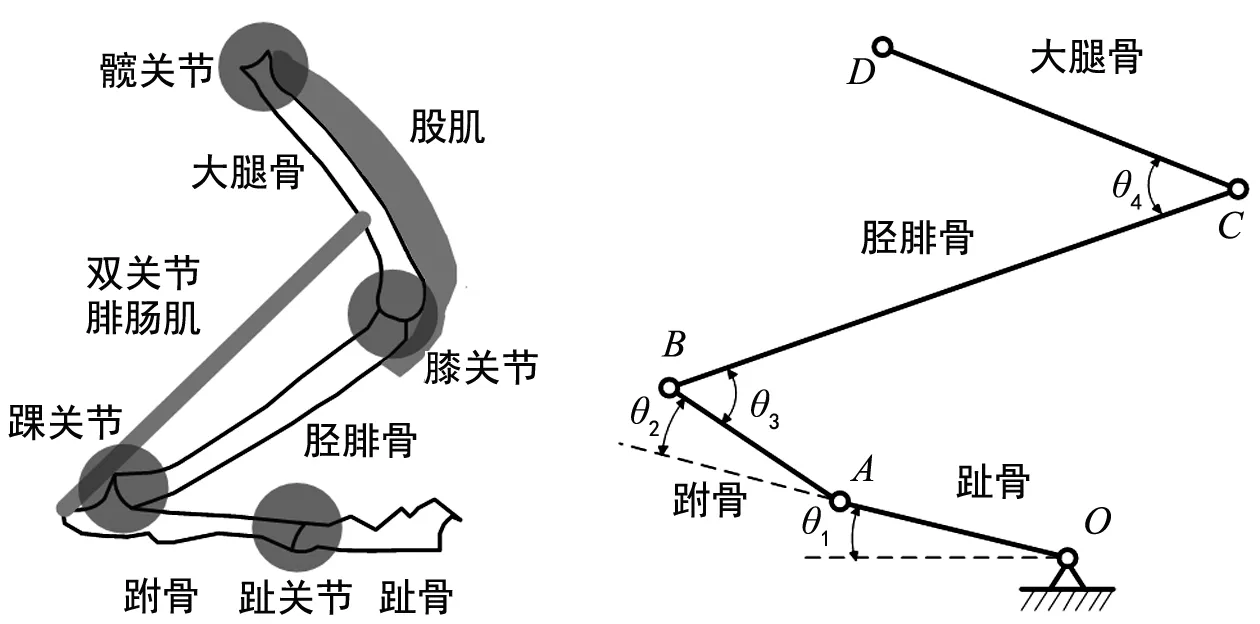
图1 松鼠后腿的生物结构模型 图2 松鼠后腿的生物运动简化模型

1.2 关节转角测量和生物参数提取

搭建松鼠跳跃运动特征提取平台，包括标尺、光源、高速相机和图像分析计算机等。利用高速相机以200帧/秒的频率对松鼠起跳阶段腿部运动进行拍摄，得到时间间隔5 ms的松鼠起跳阶段腿部运动图片，如图3所示。

图3 松鼠起跳阶段腿部运动图片(部分)

测量图片中各关节转角，得到关节角度的离散值，通过多项式曲线拟合得到各关节角度的变化曲线，如图4所示。可以看出，在跳跃起始的0～30 ms时间内，膝关节角度几乎不变，脚趾与地面的夹角也保持为零，即脚趾与地面保持贴合，踝关节和趾关节的角度变化范围均在60°左右，此阶段肢体位移变化较小，主要为肌肉储存能量和调整起跳姿态做准备；30～80 ms时间内，股肌迅速收缩，双关节腓肠肌内存储的能量也迅速释放，各关节迅速协调展开，使整个身体在较短时间内获得最大的起跳速度。

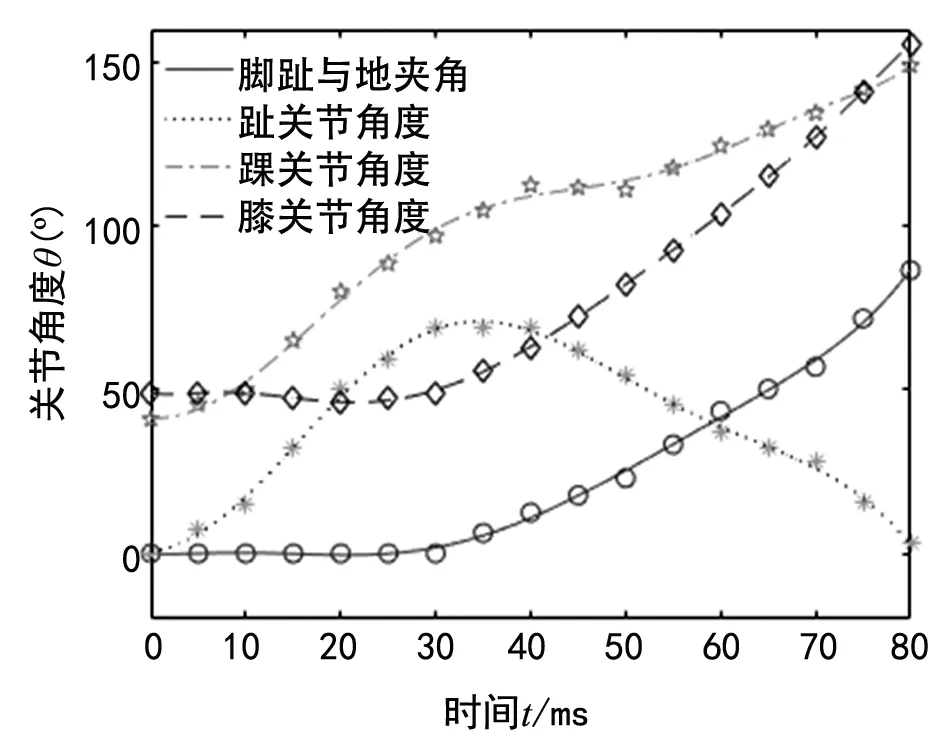
图4 关节角度的变化曲线

为进一步对松鼠跳跃模型进行运动学和动力学分析，定量地研究松鼠腿部运动的各项物理参数，通过生物解剖提取松鼠腿部的结构参数，包括各肢体的长度和质量，如表1所示。

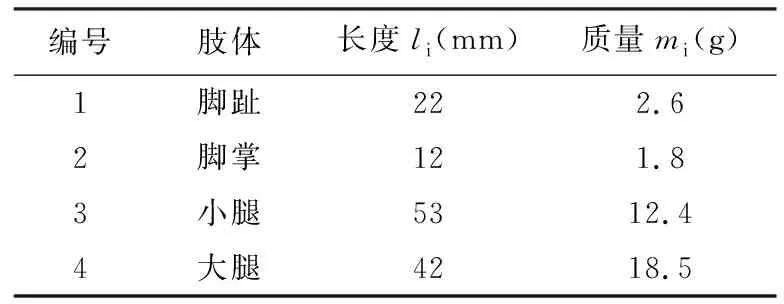
表1 松鼠后腿的结构参数

2 跳跃机构建模与分析仿真

对松鼠后腿的机构运动模型进行运动学和动力学分析，获得其位移、速度、关节驱动力矩等物理参数的变化情况，并与实际生物跳跃模型进行对比，检验模型的正确性。

2.1 运动学建模与分析

根据松鼠跳跃视频可知，松鼠的跳跃轨迹在竖直平面内，因此，松鼠后腿的各个关节均可简化为自由度为1的转动副。仿松鼠跳跃腿部机构运动模型如图5所示，其中，刚性连杆1～4分别为趾骨1、跗骨2、胫腓骨3及大腿骨4。连杆1绕固定点O转动，连杆1和连杆2之间绕趾关节A转动，连杆2和连杆3之间绕踝关节B转动，连杆3和连杆4之间绕膝关节C转动，D点为髋关节。

D-H矩阵法是分析机器人运动常用的一种方法，通过在机器人的每个构件上建立一个固定坐标系，用齐次变换矩阵来描述相邻两个构件之间的位置关系，再通过各变换矩阵依次相乘得到机器人的总变换矩阵，从而推导出末端执行机构相对于基坐标系的位姿，进而建立机器人的运动学方程。基于松鼠腿部的机构运动模型，建立跳跃机构的D-H矩阵参考系，如图5所示。

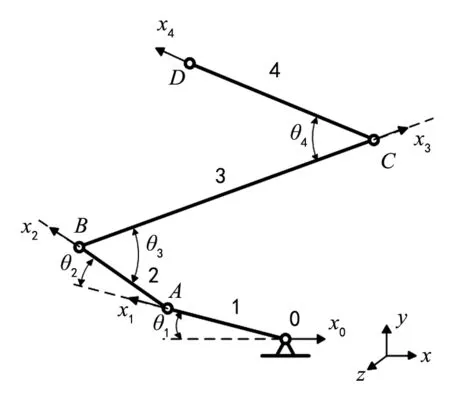
图5 松鼠跳跃腿部机构运动模型

由图5中各杆件之间的相对坐标系位置关系可求得，仿松鼠跳跃机构相邻杆件的坐标变换矩阵为：

(1)

(2)

(3)

(4)

跳跃机构的总变换矩阵为：

(5)

其中：(px,py)表示髋关节的位置坐标，

px=-l4cos(θ1+θ2-θ3+θ4)+l3cos(θ1+θ2-θ3) -l2cos(θ1+θ2)-l1cos(θ1)

py=l4sin(θ1+θ2-θ3+θ4)-l3sin(θ1+θ2-

θ3)+l2sin(θ1+θ2)+l1sin(θ1)

(6)

将表1中的生物结构参数和图4中起跳阶段关节转角数据代入求得的机构运动学表达式，通过MATLAB编程软件得到松鼠起跳阶段腿部各肢体的运动轨迹和髋关节的位移变化曲线，如图6和图7所示。与松鼠跳跃录像中的腿部轨迹对比，二者基本相符，证明了运动学分析的正确性。

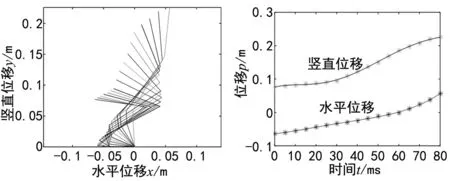
图6 腿部运动轨迹 图7 髋关节位移曲线

跳跃机器人的性能与其起跳速度及跳跃高度密切相关，因此分析跳跃机构的微分运动是进行运动学分析不可或缺的一项。研究机器人的微分运动最常用的方法是“雅可比矩阵法”，雅可比矩阵表示机构部件随时间变化的几何关系，它可以将各个关节的微分运动或者速度转化为末端执行机构的微分运动或速度，即

[D]=[J][Dθ]

(7)

其中：[D]为所求机构或标记点的微分运动矩阵；[J]为雅可比矩阵；[Dθ]为关节的微分运动矩阵。

对于仿松鼠跳跃机构，我们以髋关节处为研究对象，通过雅可比矩阵求解髋关节相对于趾尖的速度，即：

(8)

其中：雅可比矩阵[J]可以由坐标变换矩阵求得[10]，对图4 中通过多项式拟合得到的关节角度曲线方程微分，可以得到关节的微分运动矩阵[Dθ]。通过数值运算得到起跳阶段髋关节的速度变化曲线，如图8所示。

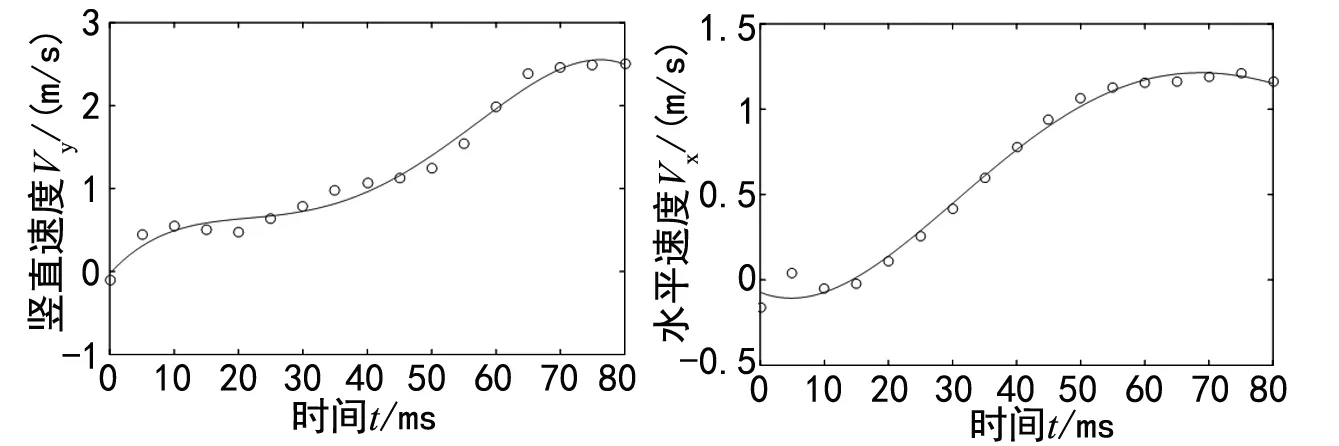
图8 起跳阶段髋关节速度曲线

从图8可以看出，整个起跳过程可分为三个阶段：在起跳初期(0～20 ms)，髋关节速度变化并不明显，此阶段主要为肌肉蓄能及调整跳跃姿态做准备；在起跳中期(20～65 ms),在股肌迅速收缩的驱动下，各关节迅速展开，髋关节速度快速增加，获得足够大的起跳速度；在起跳末期(65～80 ms)，由于股肌和双关节腓肠肌内储存的能量逐渐释放，柔性脚趾与地面的接触面积减小，地面对腿部的反作用力迅速减小，身体不再加速运动，而是以稳定的起跳速度离开地面，同时调整起跳姿态。

2.2 动力学分析与仿真

采用拉格朗日函数法建立仿松鼠跳跃机构的动力学方程，并进行动力学分析与仿真。对于多自由度机器人的动力学方程求解，首先计算连杆和关节的动能和势能来定义拉格朗日函数，然后对各关节变量求导得到关节的驱动力矩。一般多轴机器人最终的动力学方程可归纳[10]为：

(9)

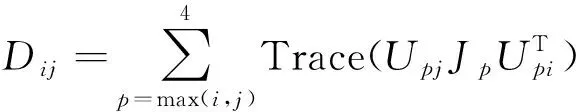
通过编程计算可以得到起跳阶段松鼠后腿各关节的驱动力矩的离散值，经曲线拟合得到驱动力矩的变化曲线，如图9所示。

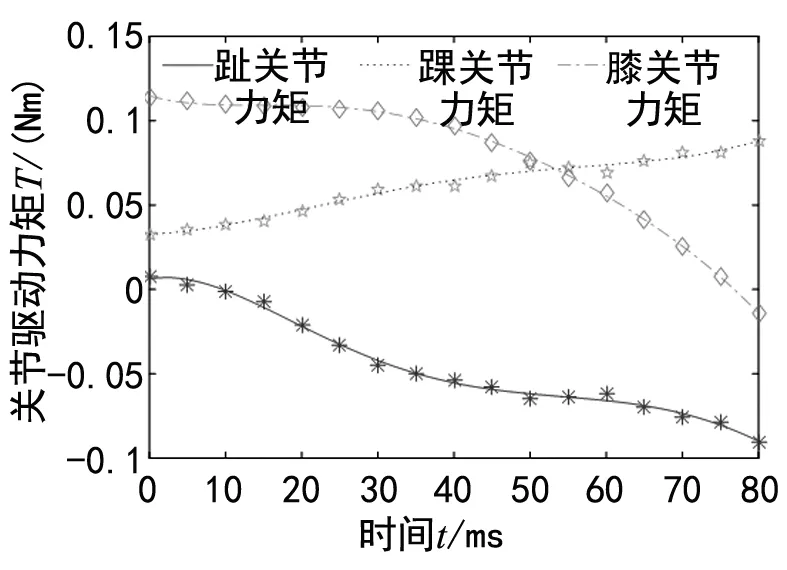
图9 跳跃运动模型关节驱动力矩

从图中可以看出，在起跳的初期阶段，膝关节的驱动力矩约为踝关节和趾关节的2～3倍，表明股肌收缩带动胫腓骨绕膝关节转动，为跳跃运动提供了大部分动力；随着股肌中能量的释放，膝关节驱动力矩逐渐减小，此时松鼠主要依靠踝关节和趾关节的转动带动柔性长脚蹬离地面，达到所需的起跳速度。

根据松鼠腿部的骨骼模型，建立如图10的机构模型，根据松鼠腿部各部分的生物参数设置刚性杆件的属性，将以上动力学数值分析结果施加在模型的转动铰链上，在Adams软件中进行仿真分析。由分析结果可以看出，机构的运动情况与松鼠的跳跃视频基本符合，验证了以上运动学和动力学分析的正确性，为后续控制系统的设计提供参考依据。

图10 虚拟样机仿真结果

3 仿生跳跃机构设计与仿真

基于松鼠腿部的生理结构体征，从仿生设计的角度出发，用刚性连杆模拟松鼠腿部的骨骼结构，各段连杆通过转动铰链连接；用拉簧模拟双关节腓肠肌，以实现其储能和弹性连杆的作用；松鼠的柔性长脚在起跳过程中主要起缓冲及延长离地时间的作用，帮助松鼠以最大速度起跳，可以采用在趾关节处设置扭簧来近似模拟松鼠的柔性长脚，以延长跳跃机构的起跳时间，防止其提前起跳。驱动器设置在膝关节处，通过小腿相对大腿绕膝关节转动实现机构跳跃。仿生设计的跳跃机构如图11所示。

图11 仿松鼠跳跃机器人模型

将三维模型导入虚拟样机仿真软件Adams中，各关节均设置为单自由度转动铰链，定义跳跃机构与底板刚性接触，设置拉簧的弹性系数k1=5 N/mm，扭簧的弹性系数k2=1.5 N·mm/(°)，在膝关节处施加扭矩τ=300 N·mm，得到仿真结果如图12所示。

图12 仿松鼠跳跃机构虚拟样机仿真

对仿真结果进行分析，得到髋关节处的速度曲线，如图13所示，与图8中松鼠跳跃的速度分析结果进行对比，两者的变化趋势基本相同，验证了所设计模型的可行性及仿生设计的合理性。

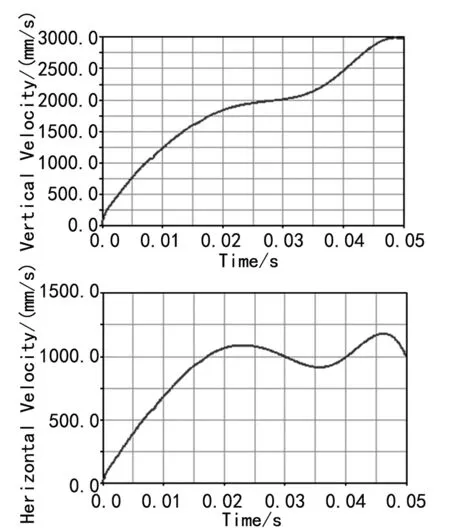
图13 仿松鼠跳跃机构运动速度曲线

图14显示的是仿松鼠跳跃机构离地后的运动轨迹，从图中可以看出，跳跃机构离地后的运动轨迹近似为抛物线，最大跳跃高度约40 cm，证明了该跳跃机构设计的可行性。

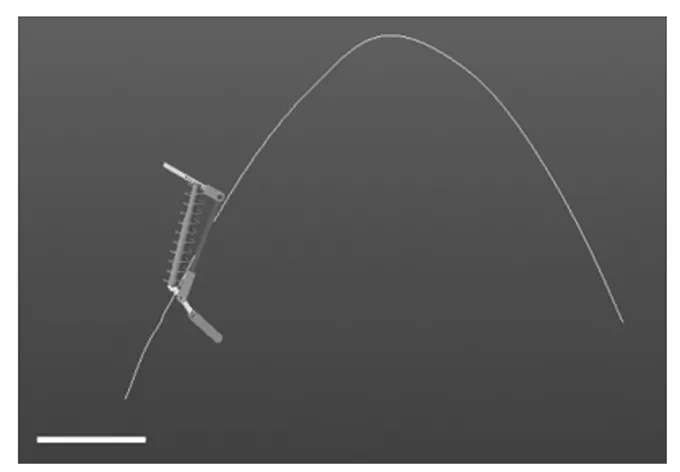
图14 仿松鼠机器人跳跃运动轨迹

4 结 论

通过对松鼠后腿的生理结构和运动机理进行分析，以松鼠腿部骨骼为基础建立生物运动模型。通过运动学分析，得到起跳阶段腿部运动轨迹和髋关节速度曲线；对模型进行动力学分析，得到各关节的驱动力矩，并在虚拟样机中进行仿真，为控制系统的设计提供依据。考虑松鼠后腿弹性肌肉和柔性脚在起跳过程中的作用，仿生设计一种柔性跳跃机构，通过虚拟样机仿真分析，证明该机构能有效模拟松鼠的跳跃特性，为进一步研究松鼠腿部变机械增益机构，提高跳跃运动效率奠定基础。