平面任意曲线积分仪原理设计及理论推导*

李 杰, 贾 露

(四川西南航空职业学院，四川 成都 610400)

0 引 言

为了满足技术发展的需求，数学运算机构得到广泛的应用，如：仿图器、变换器、加法机构、乘法机构等。笔者所研究的积分仪机构也不例外，目的是解决平面内曲线的积分问题。本积分仪器[5]巧妙的将连杆、圆盘、滚子、滚轮四者合起来。当已知一条曲线在坐标系里面的运动轨迹时(并不能确定轨迹方程)，要想确定该曲线的积分数值，则可利用本仪器，通过圆盘转动和连杆移动的相互之间的耦合，计算出结果。该机构具有结构简单，测量精准度高，使用方便等特点。

1 积分仪器的结构分析

如图1所示,整个机构由连杆、滑块、导杆、圆盘、滚子和滚轮等组成[1-3]。

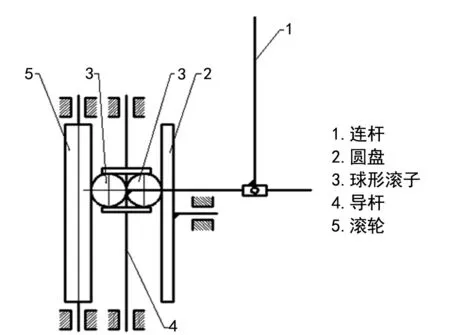
图1 积分仪器结构图

要求圆盘、滚子和滚轮之间运动传递无滑动。根据平面机构自由度计算公式，很容易计算出该机构的自由度F=2。要得到准确的输出，则需连杆尖端沿着曲线的轨迹运动的同时，圆盘做旋转运动，此二者相互耦合。最终，滚轮计算出结果。

2 积分仪器的原理分析

积分仪的简图如图2所示[3]。设：圆盘的角速度为ω2，滚子的中心到圆盘轴线的距离为h，滚轮的半径为R。则圆盘与滚子和滚子与滚轮在接触点位置的速度大小相等。

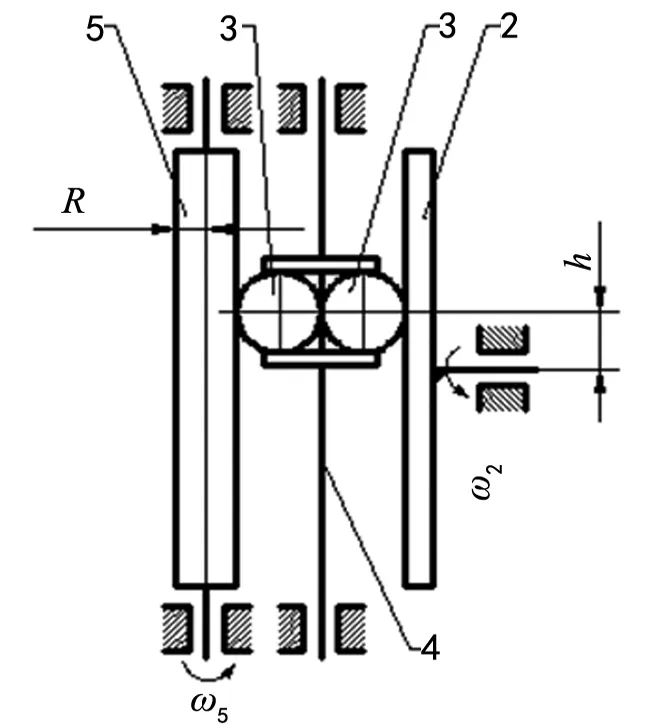
图2 积分仪原理简图

滚轮5的角速度ω5为：

(1)

设：θ5初为滚轮的初始角度；θ5终为滚轮的最终角度；θ2初为圆盘的初始角度；θ2终为圆盘的最终角度。

根据角度与角速度的关系得[6]：

当距离h与转角θ2无关时，利用公式(1)得：

(2)

当距离h与转角θ2有关时，则：h=h(θ2)，根据积分原理和公式(1)得：

(3)

积分仪是利用距离h与转角θ2有关之间的耦合进行计算。如图3[4]，首先对曲线建立坐标系，横坐标表示角度θ2，纵坐标表示垂直方向上的距离h。

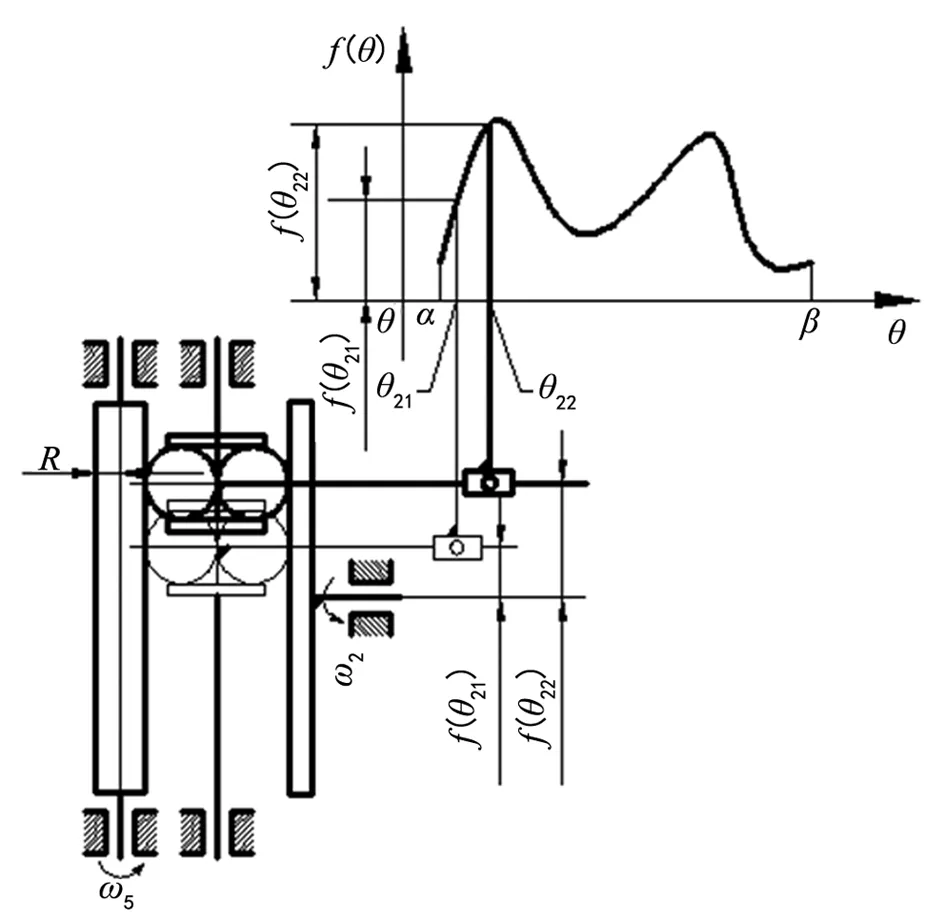
图3 积分仪原理图

设曲线的方程为f(θ2)，则h和θ2的关系式：

h=f(θ2)

(5)

当转角为θ21时，对应的函数值：

h1=f(θ21)

(6)

当转角为θ22时，对应的函数值：

h2=f(θ22)

(7)

根据公式(3)得：

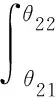
(8)

通过读取滚轮的读数θ5初和θ5终，就可计算出曲线的积分数值。

设：曲线f(θ)的积分为F(θ)，根据公式(8)得：

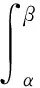
(9)

当轨迹运动到θ轴线得下方时，滚子正好在圆盘轴线得下方，滚子的旋转方向与滚子在圆盘轴线上方相反。

3 应用及结论

(1) 所研究的积分仪原理具有操作简单，实用性强等特点，为后续的研究工作打下基础，为仪器的实际运用做了理论的铺垫。

(2) 仪器求积分的问题，可利用到求解傅里叶级数中a0系数的求解。

已知一个以2π为周期的函数的轨迹(方程未知)。利用本仪器和傅里叶级数a0系数求解方程便可求得系数a0：

后续工作是再同乘法机构和三角函数机构相结合，求解出傅里叶级数中的an和bn两种系数，最终求解出傅里叶级数方程。