开挖卸荷条件下抗拔桩破坏机理及承载力分析
2019-01-18郝喆
郝 喆
(1. 辽宁大学环境学院,辽宁 沈阳 110036; 2.辽宁有色勘察研究院,辽宁 沈阳 110013)
0 引言
建筑基坑底部抗浮主要采用抗拔桩方法。随着近年来高层建筑深基坑和地下空间利用越来越多,在抗拔桩设计和施工方面已积累了丰富经验,并提出了一些有价值的计算模型和理论公式。Meyerhof[1]忽略了桩的自重,并假设在轴向拉力作用下,破坏面产生于桩土交界面处,提出了极限承载力的理论计算公式;Das[2]假设破坏面为切线与竖直方向夹角为φ/2的倒锥圆台,并据此推导出砂土中桩的极限承载力方程;何思明等[3]针对分层地基土,分析了抗拔桩的破裂面位置和形状,提出采用水平条分法计算极限承载力;Shanker等[4]认为抗拔桩的破坏面是复合剪切破坏面,并假设破坏面的边缘通过桩端,破坏面方程由桩土相互作用特性决定;Deshmukh等[5]假设桩的破坏面呈倒圆锥台形状,认为破坏面竖向土压力和破坏区桩土重力之和即为桩的抗拔承载力;黄茂松等[6]采用简化方法研究了不同桩长的扩底抗拔桩在开挖前后的极限承载力;朱碧堂等[7]推导了基于轴向Winkler地基模型的弹性解和基于同一极限摩阻力分布的弹塑性有限差分解;王之军等[8]开展了抗拔桩极限承载力的灰色理论预测分析。
以上研究主要针对桩顶位于地表或是地下很浅位置的抗拔桩,相应的工序是先开挖基坑、后施工抗拔桩。但随着工程进度要求的提高、受地层条件的限制和提高坑底稳定性的要求,抗拔桩基础先于基坑开挖施工逐渐成为发展趋势[9],而随之的上覆土层大面积卸荷,将使抗拔桩力学特性产生重大变化。目前,在开挖卸荷条件下的埋头桩模型试验上取得了一定的成果[10],但还未开展过深入的承载力理论推导。本文以沈阳地区典型砂土地层基坑工程为例,通过颗粒流数值模拟,分析抗拔桩及周边土体的破坏机理,确定破坏面形态;进一步根据极限平衡理论,推导出一般情况和开挖卸荷条件下,抗拔桩极限承载力计算公式,具有一定的理论和应用价值。
1 抗拔桩破坏形式模拟分析
1.1 抗拔桩主要破坏形式
研究表明,抗拔桩的破坏形式主要有3类[11]:与桩长等高的倒圆锥台形、沿桩土界面的圆柱形、复合剪切面(具体形式根据桩和土的特性决定)。如图1所示。
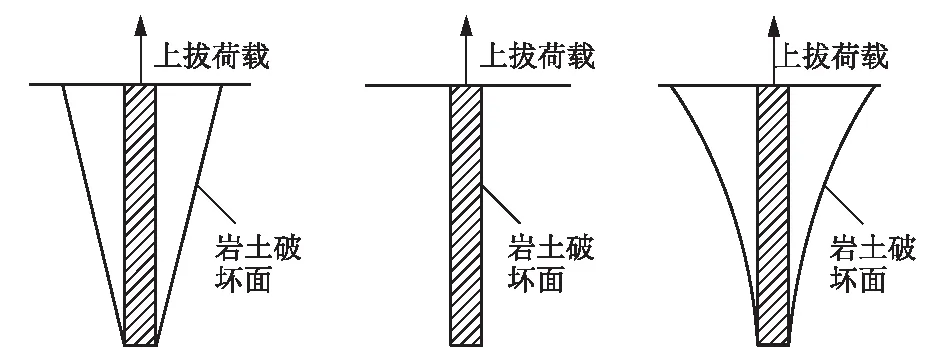
图1 抗拔桩破坏形式示意图
不同类型的地基土和抗拔桩,对应的破坏形态是不同的。本文研究是以某砂土地基中的抗拔桩工程为例,采用颗粒流数值模拟计算,确定现场抗拔桩的破坏面形态,分析抗拔桩破坏机理。
1.2 工程概况
某大型深基坑工程项目,场地位于沈阳市青年大街沈阳市府广场南侧。工程包括超高层塔楼及多层裙房,塔楼为剪力墙结构,总高度350 m;裙房为7层框架结构,高度24.5 m。工程整体设4层地下室,底板标高位于原始地下水位之下。为保证裙房建筑物的抗浮要求,设计坑底抗拔桩。为加快施工进度,施工采用先施工埋头抗拔桩后开挖基坑的工序。设计抗拔桩直径为800 mm、有效桩长为30 m,桩底相对标高为-45 m,单桩抗拔承载力特征值为2000 kN。
岩土工程勘察结果表明,区域地层由第四系杂填土、粘性土、砂类土以及第三系泥砾岩和基底花岗片麻岩组成。其中,主要地层为巨厚流砂层,以各类级配的砂为主,厚度达50~60 m。
场地地下水主要赋存在下部砂层之中,为第四系孔隙潜水,通过大气降水和地下径流实现补给。地下水位埋深在5.3~8.8 m,标高介于39.13~40.92 m,抗浮设计水位标高定为43.0 m。
1.3 计算模型建立
颗粒流方法(PFC)是继有限单元法、FLAC差分法和离散单元法等传统方法之后,新兴的一种适用于岩土介质的数值计算方法。它基于非连续介质力学原理,近年来已在岩石类材料的基本特性、岩石类介质破裂发展等基础性力学分析中得到应用[12]。与其它典型的数值计算方法相比,该方法目前应用还不太广泛,尤其在土体中的应用还比较少。鉴于砂土地层本身的颗粒状结构特性,应用颗粒流模拟具有较好的效果。颗粒流方法中,土体采用刚性圆形颗粒集合体来模拟,颗粒单元之间采用合理的接触参数,通过一定的接触特性相互连接[13]。图2为模拟计算简图。

图2 抗拔桩颗粒流计算简图
1.4 计算结果分析
建立不同桩长的抗拔桩模型,分析上覆荷载卸载前后的工况,计算抗拔桩的位移矢量图如图3所示。图中桩长a>b>c,图中的箭头簇,表示砂土颗粒的总位移矢量。
从图中可见:
(1)在上拔荷载作用下,桩周土体发生较大的向上位移;在扰动土体与原始土体之间,存在显著的线性分界线,构成桩周土的破坏界面。破坏面形态为典型的倒锥台形,分布在砂土土层中。
(2)据(a)、(c)、(e)图,(b)、(d)、(f)图的位移矢量对比可见,随着桩长的增加,破坏角α逐渐变小;据卸荷前后的位移矢量图对比中可见,桩长一致时,卸荷前后桩周土破坏角保持不变。

图3抗拔桩位移矢量图
据上述颗粒流模型计算结果,可得出不同工况条件下抗拔桩桩周土的破坏形态及破坏角,为下面的极限承载力理论分析提供依据。
2 抗拔桩承载力理论分析
2.1 一般情况下的承载力分析
据颗粒流模拟得出的破坏面特征,假定:极限荷载作用下,抗拔桩为倒圆锥台形破坏特征,且破坏面通过桩端边缘相切。设破裂面与地表面的夹角为θ,上拔力为p。据此建立非埋头普通情况下的极限平衡法计算简图如图4。
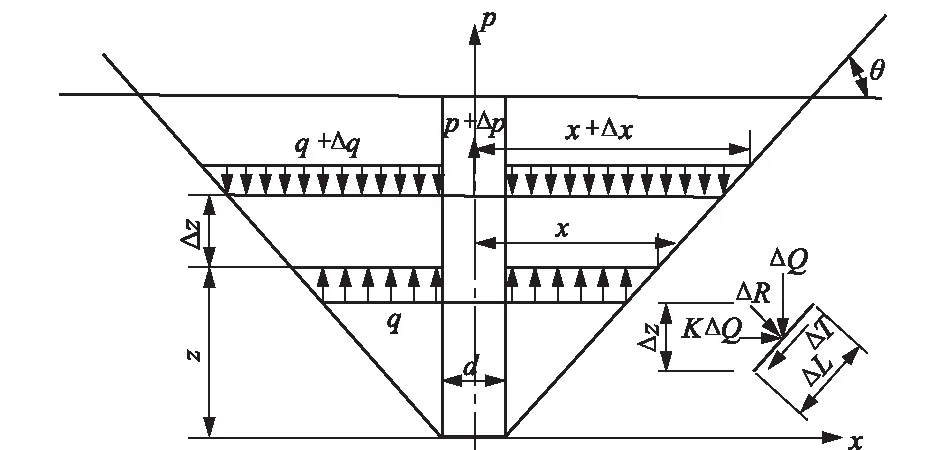
图4 一般抗拔桩承载力计算简图
据此,构造抗拔桩的破裂面方程:
x=d/2+z/tanθ
(1)
在极限平衡状态下,抗拔桩的极限上拔力、破坏面上的极限抗力、破坏面内的桩土重力相平衡。
取破坏面上的单元体进行分析。设法向应力为ΔR,切向阻力为ΔT,长度为ΔL,由Mohr-Coulomb准则得到ΔT=ΔRtanφ,列平衡方程,可以得到:
ΔR=ΔQcosθ+KΔQsinθ
(2)
ΔQ=γ(L-z-Δz/2)ΔL
(3)
式中:γ——土层的平均重度;L——抗拔桩桩长;K——侧压力系数;ΔQ——微分单元重力。
将式(3)代入式(2),得到:
ΔR=γ(L-z-Δz/2)(cosθ+Ksinθ)Δz/sinθ
(4)
则有:
ΔT=γ(L-z-Δz/2)(cosθ+Ksinθ)Δztanφ/sinθ
(5)
根据单元体的静力平衡关系:
P+ΔP-P+qπx2-qπd2/4-
(q+Δq)π(x+Δx)2+(q+Δq)πd2/4-
ΔW-2π(x+Δx/2)ΔTsinθ=0
式中:Δq=-γΔz。
对承载力与桩长求微分:
(6)
去除其中的高阶项得到:
(7)
将(1)式代入(7)中,有:
W/L+πdγL〔cosθ+(1-sinθ)sinθ〕tanφ+
2πzγLcotθ〔cosθ+(1-sinθ)sinθ〕tanφ-
πdγz〔cosθ+(1-sinθ)sinθ〕tanφ-
2πzγz2cotθ〔cosθ+(1-sinθ)sinθ〕tanφ
(8)
式中:q=γ(L-z)。
将式(8)进行积分得到单桩的极限承载力P:
P=W+πdγL2/2·〔cosθ+(1-sinθ)sinθ〕tanφ+
πγL3/3·cotθ〔cosθ+(1-sinθ)sinθ〕tanφ
(9)
将λ=L/d代入上式,得:
P=W+πγL3/(2λ)·〔cosθ+(1-sinθ)sinθ〕tanφ+
πγL3/3·cotθ〔cosθ+(1-sinθ)sinθ〕tanφ
(10)
式中:P——抗拔桩极限承载力;W——桩体自重;d——桩身直径;λ——桩长细比;θ——破裂面与水平面的角度;φ——地层摩擦角。
由式(10)可见,在某种地层,地层摩擦角与桩的破裂面角度不变的情况下,抗拔桩的极限抗拔力与桩长的立方成正比。
2.2 开挖卸荷条件下的承载力分析
参考文献[10]中,开展了开挖卸荷对抗拔桩承载力影响的模型试验,结果表明:桩顶下约20d处达桩侧阻力的临界深度,在临界深度以下的桩侧极限摩阻力变化较小。
在上述模型假定的基础上,可将开挖之前上方土层的自重荷载简化为均布荷载q′,作用在开挖底面上,得埋头抗拔桩的极限平衡法计算简图如图5。
据静力平衡可得:
ΔR=ΔQcosθ+KΔQsinθ
(11)
ΔQ=〔γ(L-z-Δz/2)+q′〕ΔL
(12)
将式(12)代入式(11),得到:
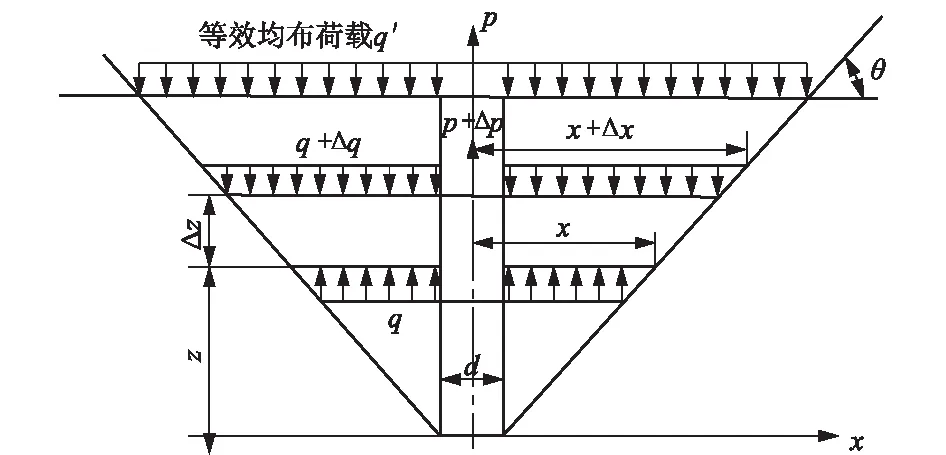
图5 埋头抗拔桩承载力计算简图
(13)
则有:
ΔT=〔γ(L-z-Δz/2)+q′〕(cosθ+Ksinθ)Δztanφ/sinθ
(14)
根据单元体的静力平衡关系:
P+ΔP-P+qπx2-qπd2/4-
(q+Δq)π(x+Δx)2+(q+Δq)πd2/4-
ΔW-2π(x+Δx/2)ΔTsinθ=0
对承载力与桩长求微分:
(15)
去除其中的高阶项得到:
(16)
将(1)式代入(16)式,得:
W/L+πdγL〔cosθ+(1-sinφ)sinθ〕tanφ+
2πzγLcotθ〔cosθ+(1-sinφ)sinθ〕tanφ-
πdγz〔cosθ+(1-sinφ)sinθ〕tanφ-
2πzγz2cotθ〔cosθ+(1-sinφ)sinθ〕tanφ+
πdq′tanφ〔cosθ+(1-sinφ)sinθ〕tanφ+
2πzq′cotθ〔cosθ+(1-sinφ)sinθ〕tanφ
(17)
将(17)式进行积分,得桩基极限抗拔承载力P0:
P0=W+πdγL2/2·〔cosθ+(1-sinφ)sinφ〕tanφ+
πγL3/3·cotθ〔cosθ+(1-sinφ)sinθ〕tanφ+
πdq′Ltanφ〔cosθ+(1-sinφ)sinθ〕tanφ+
πL2q′cotθ〔cosθ+(1-sinφ)sinθ〕tanφ
(18)
较开挖后的承载力损失Ps为:
Ps= πdq′Ltanφ〔cosθ+(1-sinφ)sinθ〕tanφ+
πL2q′cotθ〔cosθ+(1-sinφ)sinθ〕tanφ
(19)
式中:q′——开挖卸荷平均值,若开挖深度为z′,则q′=γz′。
由公式(19)可见:在某种地层,地层摩擦角与桩的破裂面角度不变的情况下,对同一桩长的抗拔桩开挖后抗拔桩的极限抗拔力损失与基坑开挖深度成正比。
则承载力损失比ξ为:
ξ=Ps/P0
(20)
上述公式中,若基坑开挖深度超过20d,开挖深度H按20d计算。
2.3 理论分析结果验证
依据文献[10]中的抗拔桩承载力损失模型试验,对本文的理论分析结果进行验证。
在使用分层落雨法测试过程中,每一层砂高度15 cm,漏斗底部与砂面距离保持50 cm。砂土干密度1.55 g/cm3(相对密实度dr=42%),砂土内摩擦角为38°
模型桩直径d=30 mm,壁厚3 mm,长度1.7 m,桩顶通过量力环连接来确定桩的极限承载力。据桩土界面剪切试验,得出桩身与砂土界面的摩擦角为31°。
模型试验槽采用圆形钢桶制作,槽子深度1.8 m,槽内径1 m,槽壁厚1 cm。通过在抗拔桩外侧设置PVC套管,实现对该范围内土体侧摩阻力的扣除,套管的外径为39 mm、壁厚为1 mm。
进行了全断面开挖深度H为30 cm、坑底以下有效桩长L为60 cm的试验,试验得到桩的承载力损失为42%。
根据公式(19)和(18),计算开挖后的承载力损失和桩基极限抗拔承载力,得到承载力的损失比ξ约为:ξ=Ps/P0=134/268=50%,与试验结果相近,证明本公式具有一定适应性。
3 结论
开展了开挖卸荷条件下的砂土地基中抗拔桩破坏机理及承载力理论分析,弥补了埋头抗拔桩理论研究的不足,可供桩基设计和规范修订参考。
(1)选取颗粒流数值模拟方法来确定现场抗拔桩的破坏形式,计算表明抗拔桩周边土体的破坏特征为倒锥台形,存在线性破坏面和破坏角。
(2)破坏角随着桩长的增加将逐渐变小;桩长一致时,卸荷前后桩周土破坏角保持不变。
(3)基于颗粒流的数值模拟结果,建立倒圆锥台形假定建立理论模型,推导出砂土中一般抗拔桩的承载力计算公式(10)。
(4)建立理论模型,推导出较实用的开挖卸荷条件下砂土中埋头抗拔桩的承载力计算公式(18)及其损失比计算公式(20),并针对前人的模拟试验结果,对理论公式进行了检验,证实了计算结果的可靠性。
