基于PSO-BP神经网络的基坑周边地面沉降预测方法研究

陈 晨， 靳成才， 赵富章， 潘栋彬， 朱 颖

(1.吉林大学建设工程学院，吉林 长春 130026； 2.中国建筑东北设计研究院有限公司，辽宁 沈阳 110006)

0 引言

随着我国城市地下空间建设的快速发展，基坑的开挖面积与深度正在逐渐增加，基坑周边土体会在基坑的开挖过程中发生沉降，地面沉降变形将对基坑周边建筑物、地下构筑物和管线的安全性造成较大影响[1-2]。图1展示了基坑开挖导致地层变形后引起地面不均匀沉降，从而导致相邻构筑物受到损坏的现象。

图1 基坑开挖后周边建筑物的变形行为

基坑周边地面沉降受多种因素共同影响，变形监测数据呈现出非线性的特征[3]，因此采用非线性映射能力强的变形监测模型来进行基坑周边地面沉降分析与预测对保证基坑周边建筑物安全性有重要意义[4-5]。目前已有部分学者运用神经网络对基坑支护结构变形或基坑底部沉降进行预测，但对由基坑开挖而引起的周边地层沉降预测研究基本处于空白阶段，本文选取粒子群算法优化的BP神经网络建立了基坑周边地面沉降预测模型，分别采用地面沉降历史监测数据和主要变形影响因素作为预测模型的输入值，建立了基于时序和基于沉降影响因素的两种神经网络模型，并在基于沉降影响因素的网络模型的基础上加入历史监测数据作为模型输入层进行神经网络模型优化，建立了综合考虑时间效应和空间效应的组合预测模型，并对3种神经网络预测模型的预测结果进行了分析比较。

1 PSO-BP神经网络

1.1 BP神经网络简介

BP(Back Propagation)神经网络是由Rumelhart和McClelland等学者在1986年提出的一种多层前馈网络[6]，其训练方法为图2所示的误差反向传播算法。BP神经网络的优点是结构简单且非线性拟合能力好，已在工程领域得到了广泛应用，但其试算过程复杂，对初始权重敏感，网络往往具有不可重现性[7]。

1.2 PSO-BP神经网络模型设计

粒子群算法(Particle Swarm Optimization，PSO)是学者Kennedy和Eberhart于1995 年根据鸟群在飞行过程中整体不会产生混乱的现象而提出的算法[8]，这种算法具有设置参数少、结构简单、无需

图2 误差反向传播算法流程

梯度信息和鲁棒性良好的特点。本文以粒子群算法中的快速寻优方式代替原有BP神经网络梯度下降训练法[9]从而形成PSO-BP神经网络，具体过程如下：

(1)设置BP神经网络初始结构。

(2)在粒子数为N的可解D维空间中，第i个粒子在寻优历史轨迹找到的适应度值最优位置被称作个体极值Pp，Pp=(Pi1，Pi2，…,PiD)T，i=1，2，…,N；将空间中N个粒子寻到的最优位置集合起来称为全局极值Pg，Pg=(Pg1，Pg2，…,PgD)T，粒子会在搜寻到这两个最优值后对自己的速度和位置通过公式(1)和(2)的方式进行更新[10-11]：

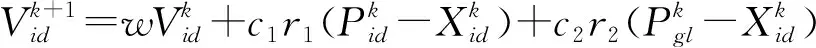
(1)

(2)

式中：d=1,2,…,D，i=1,2,…,N；c1、c2——学习因子，本文取c1=c2=1.494；r1、r2——[0,1]的随机数；k——当前迭代次数；Vid——第i个粒子进行第K次迭代时的第d维速度；w——惯性权重，能够以防止计算过程陷入局部最优为目的调节粒子当前速度，根据收敛效果较好的ClercPSO模型w取0.792[12]。

网络模型的种群粒子数被设置为20，所有粒子维数均为2，算法迭代进化共计50次。

(3)神经网络的预测输出与期望输出的均方误差作为粒子的适应度函数。比较适应度和Pp与Pg直至全局最优的适应度值小于设定值或最大迭代次数时训练结束。

2 基于时序的PSO-BP神经网络模型

2.1 工程概况

项目位于上海市浦东新区，属滨海平原类型地貌，施工区域总面积为2.83 km2。本工程通过GPS监测技术对基坑周边地面沉降进行监测，将122个编号为C1～C122的监测断面布置于施工区域周边，断面间距为80～100 m，每个监测断面布置3个监测点，共布置监测点366个。本文选取施工区域内某基坑作为研究对象，基坑面积2947 m2，周长252 m，设计深度7.10 m。基坑采用内侧设置2Ø700 mm水泥土搅拌桩形成帷幕的方式进行支护，地层主要由人工填土、粉质粘土、粘质粉土、淤泥质粘土组成，地下水稳定水位埋深0.50～1.20 m，局部存在浜填土及明塘。自2016年5月23日起开始对基坑周边的路面进行沉降监测，监测频率约为7 d一次，C62断面和C63断面的累计沉降监测值如图3所示。本文选取具有代表性的C62-2监测点和C63-2监测点监测数据，采用基于PSO-BP的神经网络模型对地面沉降量进行预测。

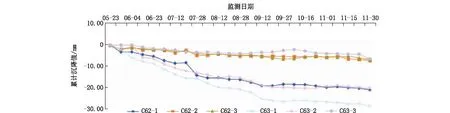
图3 C62、C63监测断面累计沉降曲线

2.2 神经网络模型建立

基于时序的PSO-BP神经网络模型参数的选取原则为在保证模型预测精度的同时使网络的结构尽量简单以免计算速度缓慢[13]。随着时间的推移，基坑开挖后周边地面沉降量逐渐增大，其主要原因是基坑周边土体的应力释放会在开挖过程中产生变化，因此推断连续的时间序列与基坑周边地面随时序所产生的沉降量数据间存在一定的相关性，可依据历史数据之间的内在规律性对沉降量进行预测[14-15]。本文将施工过程中得到的某一时间段内沉降量监测数据记为序列S(1)，S(2)，…，S(n)，这一时间段之后的沉降监测数据序列记为S(n+1),S(n+2), …。在序列S(1)，S(2)，…，S(n)中，选取m次监测数据作为神经网络的输入向量来构造训练样本，并将第m+1个时间点的监测数据S(m+1)作为网络模型输出值，共组建出n-m组训练样本与预测目标值并进行训练，再将S(n-m+1)，S(n-m+2)，…，S(n)序列输入到已经训练好的PSO-BP神经网络模型即可计算出S(n+1)的预测值。

基于时序的PSO-BP神经网络模型在输入层节点数m取10时，能够保证预测精度较高且所需计算量较少。神经网络的初始结构中隐含层个数和节点数对网络性能有较大影响，通过对一个隐含层和两个隐含层不同节点训练时间和计算结果的对比分析，单隐含层的预测精度能满足要求，而且训练时间更短，隐含层节点为11时效果最好，故本文的PSO-BP模型选择如图4所示的10-11-1的网络结构。

图4 基于时序的PSO-BP神经网络结构

2.3 预测结果分析

网络模型选择C62-2与C63-2监测点5月23日-8月28日地面沉降数据进行训练，训练结束并得出神经网络模型后根据上文所述方法对9月5日-11月1日的累计地面沉降量进行预测。运用基于时序的PSO-BP神经网络模型得出的预测误差以及预测值和实际值的对比结果如表1和图5所示。

表1 C62-2与C63-2监测点沉降预测结果

图5 基于时序的PSO-BP预测方法预测值与实测值对比

由图5可知，对于C62-2监测点，预测值相对误差范围为-7.32%～10.57%，平均相对误差为3.72%，残差绝对值均小于0.5 mm。对于C63-2监测点，预测值相对误差范围为-5.33%～8.31%，平均相对误差为4.38%，残差绝对值均值为0.8 mm左右。整体上预测精度较高，相对误差波动较小，因此基于时序的PSO-BO神经网络模型能满足实际基坑工程中对周边地面沉降预测的要求。

3 基于沉降影响因素的PSO-BP神经网络模型

3.1 神经网络模型建立

基坑周边地面沉降变形的影响因素如图6所示，其中每种因素都具有影响程度不确定性强的特点[16-17]，传统方法往往难以基于这些因素对沉降变形进行准确预测，而基于沉降影响因素的PSO-BP神经网络模型以其非线性拟合能力强的特点为预测提供了可行方案。

本文采用开挖过程中某一阶段开挖面以上地层内摩擦角φ、土体粘聚力c、土体重度γ、地层渗透系数k的加权平均值以及基坑实时开挖深度h、监测点与基坑槽边的距离d共计6项影响因素作神经网络输入层，并将这一阶段的沉降量实测值作为神经网络预测目标进行训练，隐含层节点数同上，网络模型选择如图7所示的6-11-1的网络结构。

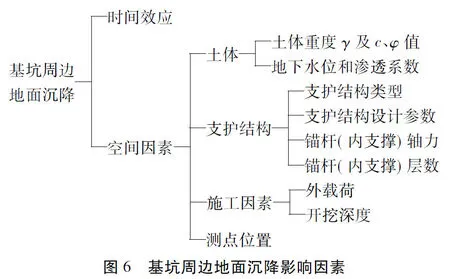
图6基坑周边地面沉降影响因素

图7 基于沉降影响因素的PSO-BP神经网络结构

3.2 预测结果分析

网络模型选择C62-2与C63-2监测点5月23日-8月28日共计12组地面沉降数据进行训练，训练样本中沉降影响因素如表2所示，根据训练结束后得出的基于沉降影响因素的PSO-BP神经网络模型和本文3.1节所述方法对9月5日-11月1日的累计地面沉降量进行预测，整个周期内包括了开挖前、开挖和基坑施工后3种工况。

根据图8的预测结果可知，对于C62-2监测点，基于沉降影响因素的PSO-BP网络模型的预测值相对误差范围为-10.89%～9.91%，平均相对误差为6.87%，对于C63-2监测点，相对误差范围为-14.08%～6.39%，平均相对误差为6.06%。基于沉降影响因素的PSO-BP网络模型的预测值在可以接受的范围之内，对于基坑变形的动态预测来说满足要求，也说明影响变形的参数选取比较合理。但是相较于基于时序的神经网络模型，该模型所得出的各点预测值相对于监测值的波动较大，虽然输入层节点数较少，但模型所需参数类型和数值更多，需获取完整的现场勘察资料才能运用该模型进行预测。

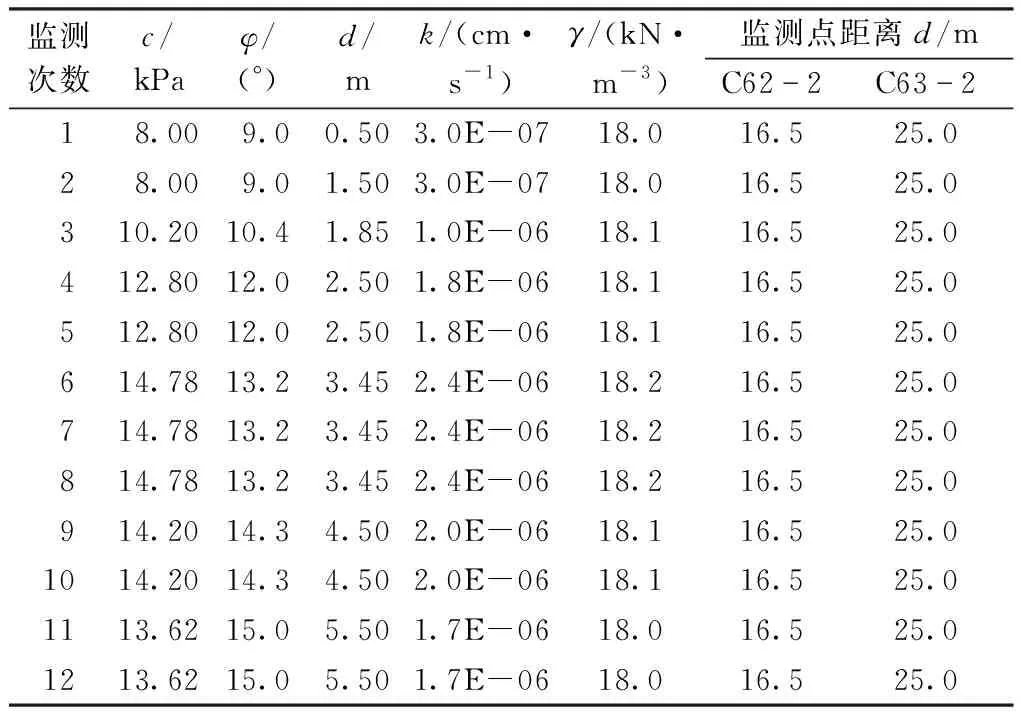
表2 基于沉降影响因素的神经网络训练样本

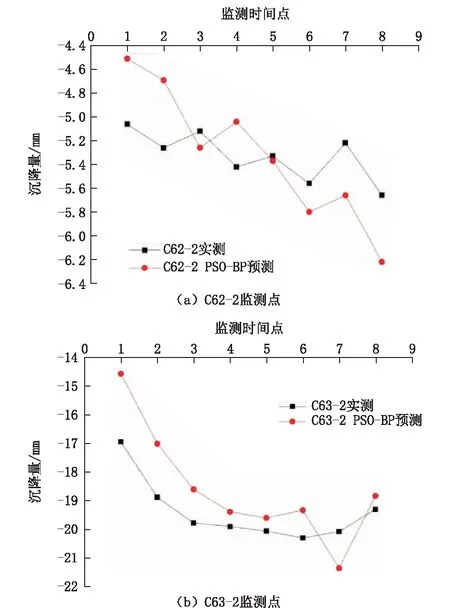
图8 C62-2与C63-2监测点预测值与实测值对比

3.3 神经网络模型优化设计

PSO-BP神经网络模型的优化设计是指在基于沉降影响因素的网络模型的基础上，将历史沉降数据填加到输入层中，形成监测数据、施工工况和周边地层参数等多源数据作为输入值的预测模型。神经网络优化模型的输入参数如图9所示，图中y1、y2、y3代表预测目标前3个监测时间点的地面沉降数据，模型选择9-11-1的网络结构。

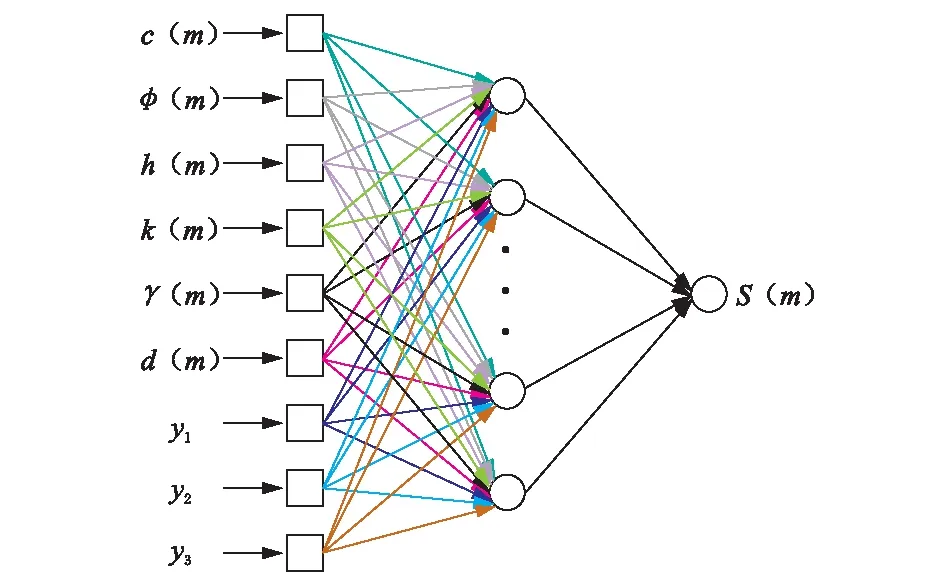
图9 PSO-BP神经网络优化模型结构

由图10预测结果可知，对于C62-2沉降监测点PSO-BP优化模型预测值相对误差范围为-7.43%～6.995%，平均相对误差为3.96%。与基于沉降影响因素的预测模型相较之下，优化模型的平均相对误差降低了2.89%，其预测值与实际值的逼近效果更好，相比于基于时序的预测模型，二者平均相对误差十分接近，但优化模型的相对误差范围更小，说明其预测结果更稳定。

图10 C62-2监测点3种模型预测值与实测值对比

由图11预测结果可知，对于C63-2沉降监测点PSO-BP优化模型预测值相对误差范围为-7.22%～4.80%，平均相对误差为3.98%，其相对误差比基于时序和基于沉降影响因素的预测模型分别降低了0.40%和2.08%，且误差波动更小，说明PSO-BP优化模型的预测结果精度更高且预测结果更加稳定。与PSO-BP优化网络模型相比，虽然采用基于时序和基于沉降影响因素模型能满足工程需要，而且可以简化网络结构，减少训练时间，但是优化后的网络模型以其准确性和实时性对复杂的基坑周边地面沉降控制具有更大的优越性。

图11 C63-2监测点3种模型预测值与实测值对比图

4 结论

(1)本文对基于时间序列以及沉降影响因素的粒子群算法优化BP神经网络模型进行了计算原理、预测步骤和模型结构的详细说明。选取上海前滩某基坑工程周边地面沉降监测数据建立了基于PSO-BP神经网络的预测模型，对基坑开挖后的周围地面沉降进行预测。C62-2与C63-2监测点基于时序的PSO-BP神经网络模型预测值平均相对误差分别为3.72%和4.38%，基于沉降影响因素的PSO-BP神经网络模型预测值平均相对误差分别为6.87%和6.06%。基于时序的神经网络具有更高的精度且二者预测误差均较小，表明PSO-BP神经网络能够很好地对基坑周边地面沉降进行分析与预测。

(2)基于沉降影响因素的PSO-BP神经网络模型预测结果可信度较高，证明模型中“开挖面以上地层内摩擦角、土体粘聚力、土体重度、地层渗透系数、基坑实时开挖深度和监测点与基坑槽边的距离”六项影响因素的选取比较合理，对施工过程中避免基坑周边地面沉降量过大起到指导作用。

(3)为了综合考虑时间效应和空间效应对于预测结果的影响，将历史监测数据加入到基于沉降影响因素的预测模型中进行神经网络优化，并采用优化后的模型进行预测分析。对于C62-2监测点优化模型预测值平均相对误差为3.96%，对于C63-2监测点预测值平均相对误差为3.98%，且相对误差范围相比于基于时序与基于沉降影响因素的PSO-BP网络模型均有减小，说明其预测结果更加稳定，预测值和实际值的逼近效果更好，其预测结果更能满足工程需求。