矿井水灾多逃生路径模型应用研究

苑亚南，朱希安，王占刚

(北京信息科技大学，北京 100101)

矿井突水与瓦斯、煤尘是矿山生产建设过程中三大主要灾害。突水事故造成了经济损失、人员伤亡以及矿井地质结构的破坏[1-2]。由于矿井中巷道分布错综复杂，巷道容量不一，当矿井涌水超过正常的排水能力时，就会发生矿井水灾事故。因此，为了保障矿井作业的安全，提高矿山应急救援效率，增强矿井抗灾救灾能力，这是处理矿井重大事故的关键[3]。

当前，我国研究矿井火灾较多，对矿井水灾的逃生路径研究的较少[3]。矿井水灾发生后，为了解决有效地组织从业人员在最短时间内安全地到达逃生出口，本文建立了一种矿井水灾多路径逃生模型。

1 多路径逃生模型整体设计

矿井突水是常见的突发性强烈的矿井灾害。目前降低水灾事故对从业人员的伤亡率是水灾救援工作的重中之重，逃生路径最优化选择是解决上述问题的有效方法之一。在选择最优路径时，巷道结构信息，矿井下从业人员数目等是不可忽略的重要条件，因为路径最短未必是最优路径的。结合水力学特性分析突水点涌水量对巷道的灌水能力，依据巷道结构特征分析几种筛选有效逃生巷道的指标，在从业人员较多的情况下，选择多路径最优可以有效地避免逃生拥挤。因此，本文设计了一种矿井水灾多路径逃生模型，如图1所示。

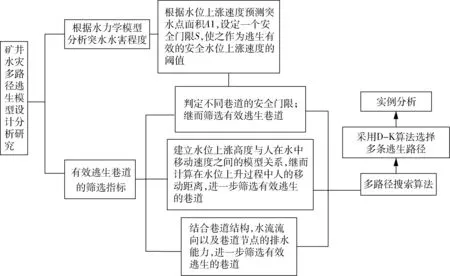
图1 矿井水灾多路径逃生模型Fig.1 Multipath escape model of mine flood

1.1 突水机理与水力学特性分析

在众多突水模式当中，其机理主要分为厚板微观压裂导生、薄板宏观整体破断导水两种。本文以断层裂隙带突水模式为对象研究其突水点水力学特性。断裂直通式突水模式如图2所示。

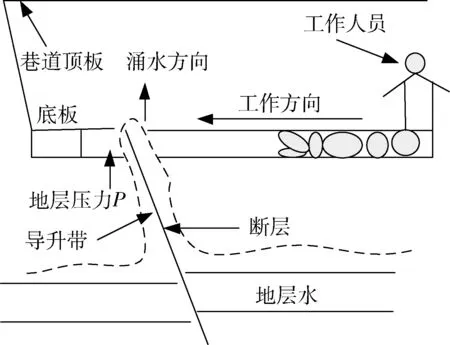
图2 断裂直通式突水模式Fig.2 Mode of water inrush through fracture

当地层水受到地层压力的影响，会沿着断层向上流动直至突破底板造成突水事故。地层压力决定了突水点处水流的速度，同时也反映出涌水量的大小及巷道水位的上升速度。由于巷道地面常常是不平的，而且存在一定的坡度，但是巷道的容积是恒定的，因此巷道水位的上升速度在一定程度上可以反映出突水点水害程度。

为了便于建立模型，简化巷道环境：①假设某节巷道地面规整无坡度；②巷道结构为长方体型；③突水点破裂面积基本不变；④地层水压稳定。因此，可以建立突水点面积数学模型，见式(1)～(3)。

(1)

(2)

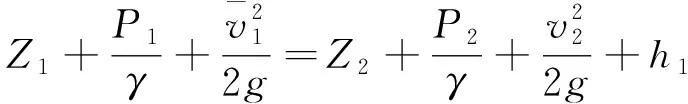
(3)

联立式(1)～(3),得出A1的方程式，见式(4)。

(4)

从式(4)可以看出，A1的大小可以通过巷道水位上升的速度反映出来。因此，水位上升速度越快，则说明突水点面积越大。

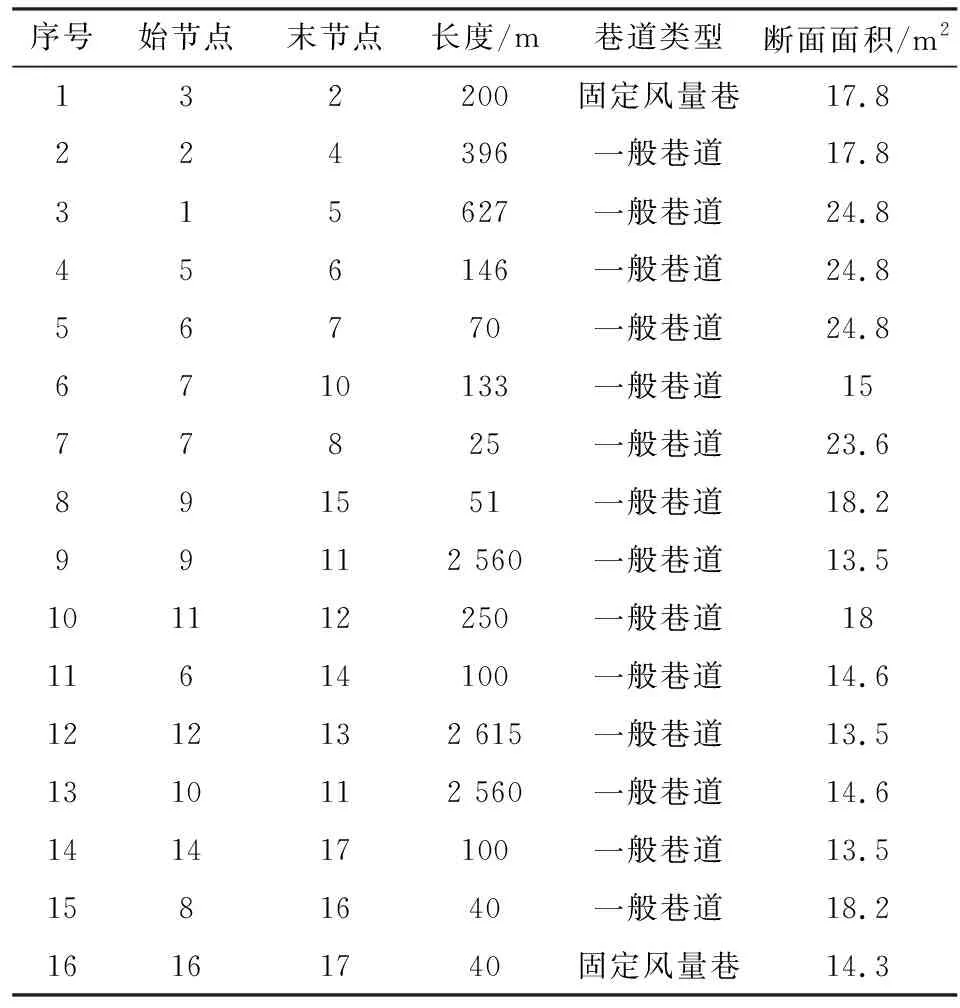
若设安全门限s使得A1

(5)

由式(5)可以看出，水位上升的速度可以作为是否启动排水系统的预警依据。其中s由巷道结构信息特征共同决定：巷道类型、巷道坡度、风向、水位高度、局部障碍物等。

1.2 有效逃生巷道的筛选指标

1.2.1 巷道安全门限s的计算方法

对于某一节巷道通过调查可以得到巷道结构信息(表1)，这些信息可以作为安全门限的影响因子。

表1 巷道安全门限s影响因子Table 1 Roadway safety threshold of S impact factors

根据表1中影响因子可以构造安全门限s(tmin)的计算方式。其中βi,j为因子从i到j的关联系数。将这些影响因子以及因子关联系数构造成一个系统，令正常情况下人从某巷道能够穿过的最短时间tmin作为输入，其输出的结果乘以一个调整因子α作为安全门限值。为了便于理解，构造的计算系统结构如图3所示。

图3 安全门限计算系统框图Fig.3 Block diagram of safety threshold calculation system

从图3中可以看出安全门限s(tmin)是一个关于逃生时间的一个函数，将此与突水点处的突水面积建立联系，就可以预测突水程度对逃生的影响。其中，影响因子通常采用巷道的通行难易系数作为实值，巷道通行难易系数可以查阅文献[4]。

1.2.2 人体水中移动速度模型

已知人在不同水位条件下移动速度不同，因此水位越高人的移动速度v3就会下降。这主要体现在人的体力衰减变化率r上，使得r随着水位高度h的增加而增加。若将r表示为h的函数r(h)，方向与移动速度相反，于是函数v3(h)写作式(6)。

v3(h)=v0-r(h)(h+1)

(6)

式中,v0为初始逃生速度。

假设人体体力衰减变化率正比于水位高度，则有式(7)，因此推导结果见式(8)。

r(h)∝h

(7)

v3(h)=

(8)

式中：r0为人体体力固有衰减系数;λ为调整因子;δ为方差。

从式(6)～(8)可以看出,人的移动速度与水位高度呈二次衰减变化规律。因此，该模型能够估计从业人员从突水点到安全节点的有效逃生时间。

1.2.3 水流流向与巷道节点排水能力

根据井下巷道的分布状况，可以分为水平巷道、垂直巷道及倾斜巷道3种。突水一旦发生，水流首先会向比突水点更低的地方蔓延，称之为下向蔓延。当水将突水点以下的巷道灌满之后，就会开始沿着突水点上开始升涨，称之为上向升涨，直至整个井下全部灌满水为止，这是矿井水流的两种基本运动特征。在下向蔓延过程中，水流运动会自动寻找最低的巷道位置。从巷道突水点到巷道最低点是水流自动寻找的路径。因此该条路径所经过的所有巷道都不应当作为选择逃生的巷道。在上向升涨过程中，在水平巷道灌水过程中，利用人体在水中的移动速度变化规律计算其逃生时间，使之判断该水平巷道是否可以作为逃生巷道的选择指标。

其中下向蔓延路径，利用有向图G(V,E,P)来表示。V为巷道节点的集合；E为节点边的集合；P为节点的空间坐标。因此通过坐标点P在垂直方向上的位置关系，利用V和E将下向蔓延的路径表示出来。

排水能力与巷道节点处的边数量有关，同时计算该节点到逃生出口的最短距离，为诸多边中寻找最佳逃生巷道提供了依据。

2 改进的D-K多路径逃生算法

在矿井突水发生后路径最优规划过程中，Dijkstra算法结合上述的巷道筛选指标可以求得从突水事故点到逃生出口的一条最优路径。事实上，矿井水灾事故造成的不可测危险，加之井下从业人数要求逃生路径不应当只有一条，而是应当需要有备用的逃生路线。因此，多路径逃生可以有效地解决上述问题。K则算法可以求解从突水点到逃生出口的前N条最优逃生路径，结合两种算法优势与筛选后的巷道集合求解出安全系数更高的逃生路径。

2.1 Dijkstra算法

Dijkstra算法是公认的最优路径经典算法之一，通常结合带权值有向图G(V,E,W)来表示。其中，V为网络拓扑所有节点的集合；E为所有边的集合；W为边的权重值。在搜索过程中，首先将所有的节点初始化为未标记点，接着遍历所有节点与之相近的节点中最短距离的标记为永久标记节点，将其他节点作为临时标记节点，最终找到距离最近的所有永久标记节点与目标节点。具体算法描述如下所示[6-7]。

步骤一：以单一给定的源节点为开始起点，遍历其所有邻接点，并计算其权值，选择权值最小的节点作为下一次搜索的起点。

步骤二：检验从所有已遍历点到其直接连接的未标记点的权值，选取最小值为遍历点到邻接点的距离，并累加从源点到邻接点的权值。

步骤三：如果遍历到的节点已经计算过距离，就比较当前新计算的距离与已计算过的距离大小，然后取其中最小值，并更新节点的信息，将现有的邻接点转为已遍历点。

步骤四：重复步骤二和步骤三，直到遍历到目标节点，其得到的距离就是其实节点的最短路径距离。

2.2 K则最短路径算法

求取K则最短路径最经典的算法是Dijkstra的去边算法，它的主旨是先利用Dijkstra算法求出起始点到终结点之间的短路径，然后依次去掉该最短路径上的任一条边，重新计算起始点到终结点之间的最短路径，最后按照权值大小依次排序，就得到了K则最短路径。具体的运算过程如下所述[8]。

步骤一：在赋权图G(V,E,W)中确定起始点和终结点Vi。

步骤二：利用经典的Dijkstra算法求出起始点Vi到终结点Vj之间的最短路径r,并求出该条路径权值D。

步骤三：统计最短路径上节点的个数n,也就是说最短路径上有n-1条边。

步骤四：去掉最短路径上的第一条边，重新利用Dijkstra算法求出起始点Vi到终结点Vj之间的最短路径，并求出对应路径的权值D1。

步骤五：依次去掉剩余的n-2条边，重新得到n-2条最短路径及对应的权值。

步骤六：对上述权值D1-Dn-1进行排序，结合最短路径权值D就得到了n条最短路径。

2.3 改进的D-K算法

D-K路径最优算法是根据Dijkstra算法和K则最短路径算法的基础上提出的一种求解前N条最优逃生路径的新算法[8-9]。通过上文1.2节中的几个指标对巷道边集合E进行了筛选，剔除了危险度较大的巷道，使得剩余的边组合的最优逃生路径安全性更高，进一步改进了D-K搜索算法，这样就增大了从业人员的逃生率。结合带权有向图G(V,E,W),具体的算法描述如下所示。

步骤一：将所有的节点确定下来，并分别标记为Vm1,Vm2,Vm3,…,Vmn,存储在集合G中;同时将边集合E确定下来并标注为Em1,Em2,Em3,…,Emn。

步骤二：结合上文的三种筛选指标对集合E中的边进行剔除，更新集合G和集合E。

步骤三：确定某一节点Vi为源节点，节点Vj为目标点。将所有从Vi到Vj中的节点保存到集合P中。其路径集合D初始化为0。

步骤四：根据Dijkstra算法求出Vi到Vj的最短路径，即第一条最短路径。将其经过的该条路径上的所有路径值保存到集合N0,将所有的边集合到E0。

步骤五：将E0的任一条边去除，更新节点集合为Gi。

步骤六：重复步骤四和步骤五，直到Vi到Vj无路可走。

步骤七：对所有的路径值进行排序，根据从业人员数量，确定前几条最优路径保留下来，算法结束。

3 改进的D-K路径搜索算法在王家岭矿的应用

2010年3月，王家岭矿在基建施工中发生透水事故。当班井下共有作业人员261人，事故发生后有108人相继升井，153人被困井下。经抢救有115人成功获救，37人死亡，1人失踪，直接经济损失900.8万元。在逃生过程中，选择最优的逃生路径可以有效地降低人员伤亡率。因此，根据王家岭矿巷道的基本结构信息，结合文中对巷道逃生性能进行评估筛选，利用改进的D-K路径搜索算法搜索王家岭矿的最优逃生路径。

根据王家岭矿井巷道布置图生成了局部网络图，为了便于试验，将其简化为节点和直线边的网络结构图(图4)。筛选出17个节点进行实验验证，其中将节点8作为突水点，节点4和节点13为目标节点。表2是王家岭矿筛选后的局部巷道结构信息。

图4 王家岭矿筛选后的巷道局部网络图Fig.4 The local network map of the laneway after Wangjialing screening

为了便于分析，将表2中的巷道用网状图加以构造。其中图4中的线段表示路径，并非等比例的，圆圈代表巷道节点。图4中1～3是主平硐，长度是12 400 m；1～2是副平硐，长度是12 250 m；9～7是通过其他未标明节点连通的路径，通过上文1.2节分析可知，其并非可取路径。

如果巷道节点8比节点16的水平位置低，分析出路径8～16在空间分布上是水流下向蔓延时的路径。如果在逃生时选择的最优路径中包含类似情况的一段或多段都会增加逃生风险。在该条路径上，根据上文1.2.3分析得到巷道的危险系数是增加的。在节点8邻近的节点中，节点7、节点9比节点16的排水能力更好一些，节点边数较多，所以逃生时选择节点7、节点9作为首要的选择。再通过计算突水节点相邻的不同巷道的安全门限值进一步筛选。因此，将上述中边去除之后的网络结构数据，利用Matlab仿真平台结合改进的D-K算法进行仿真。仿真结果见表3。

表2 王家岭矿筛选后局部巷道结构信息Table 2 Information on the structure of local laneway after screening in Wangjialing mine

表3 Matlab巷道路径筛选仿真结果Table 3 Simulation results of road path screening in Matlab alley

通过表3中分析可知,从突水点到逃生目标节点13与节点4的最优路径有三条。在考虑井下从业人员较多的情况下，这三条路径能够有效避免人员逃生时发生拥堵，能够提高井下从业人员成功逃生的机率。

4 结 语

通过对突水点的水力学分析，不同巷道安全门限的计算以巷道节点的排水能力将巷道网络组成的节点和边集合进行一次清洗，然后结合Dijkstra算法寻找一条从初始节点到目标节点的最优路径，利用K则路径最短算法选择前N条最优路径，再根据井下从业人员的数量确定最优路径的数目。本文加入了突水点水力学特性，水中逃生速度模型及突水水流流向和巷道节点排水能力进行了分析，这相对于单一化考虑巷道基本结构对逃生路径的影响更加具体，在一定程度上提高了逃生路径的安全性能。但是在巷道安全门限计算上存在一定的复杂性，这是本模型的不足之处，还需进一步改进。