基于变权综合权重的黄金洞尾矿库风险评价

李凤娟，章 光，刘明泽，贺 坤

(武汉理工大学资源与环境工程学院，湖北 武汉 430070)

0 引 言

目前，我国现有尾矿库1.2万余座。尾矿库是一个具有高势能的人造泥石流重大危险源，有严重的安全隐患，时常会发生滑坡、泥石流等重大灾害[1-2]。尾矿库一旦失事，会给周围居民带来生命财产损失，也会造成当地经济、环境严重破坏。根据美国马萨诸塞洲Clark大学灾害评价小组的报告结果，在调查的93种事故灾害隐患中，尾矿库失事高居第18位，远大于航空事故，火灾等60种灾害事故[3]。

近年来，我国学者对尾矿库事故原因及预防做了大量的分析与研究。王英博等[4]采用和声探索算法和BP神经网络建立了尾矿库安全评价模型，有效地刻画了尾矿库事故随机波动特性；郑欣等[5]将集权分析理论与层次分析法结合用于尾矿库安全评价，根据i的不同取值可反应尾矿库的具体安全状态；姜洲等[6]基于尾矿库突变机理和大量工程实践，确定了尾矿库评价指标体系及评价指标体系的等级量值区间，从而找出尾矿库的具体敏感因素；王醒等[7]采用改进的模糊评价模型计算得出某尾矿库的安全评价结果；高振兴等[8]将突变理论与模糊分析结合起来，对尾矿库进行多目标分解，得出尾矿库安全总突变级数，又将其变换得出尾矿库的安全度；陈水生[9]通过对尾矿库料物力学性质试验，尾矿库本构模型及固结理论，以及尾矿库溃坝致灾过程等的研究，提出了尾矿库重点研究方向；李全明等[10]根据实践经验，指出尾矿库安全评价应立足于有限元理论的定量评价法；张力霆等[11]利用坝体位移跟踪测量系统对尾矿库坝体溃决的演进过程进行了观测，总结了整个试验过程中的溃决模式及破坏形式；李强等[12]根据尾矿库几何特征建立了尾矿库的三维数值分析模型，实现了尾矿库基于流固耦合-强度折减的三维稳定性分析，并分析了尾矿坝滑移面的形成过程。

尾矿库失事受到很多因素的影响，但是前人在确定影响尾矿库安全运行的因素权重时，大多数采用常权综合，在实际问题中，具有片面性[13]。本文在确定因素权重时，采用主观性的层次分析法和客观性的熵权法相结合，通过构造均衡函数，引入了变权综合。先分别求出两种方法的因素权重，然后再通过构造均衡函数，引入变权综合，再对得到的因素权重求变权权重;最后引入偏好系数，将两种方法取得的变权权重结合起来，求得综合权重。变权的目的是根据因素状态之间的均衡水平调整各因素在综合决策中的作用，既注重各因素的作用，又注重各因素之间的作用，具有科学性[14-15]。通过引入偏好系数，既可以克服AHP赋值的主观性，又可以保证权重的客观性，使得到的综合权重达到主观与客观的统一。本文在确定了变权综合权重之后与风险评估相结合，建立变权综合权重风险评估模型，并将其模型应用到黄金洞尾矿库的安全评价中。

1 确定综合权重

1.1 层次分析法确定主观权重

层次分析法(AHP)是一种将定量分析与定性分析结合起来，根据不同因素之间的隶属关系和影响进行层次化条理化的处理，建立自上而下的多层次(准则层，目标层，措施层)结构模型[16]。利用决策者的经验判断各衡量目标的重要性，并给予定量，然后再根据数学方法确定每一层次因素的权重值，最后通过综合计算，得出每个因素的相对重要性并进行排序，作为评价和选择的依据。具体计算步骤如下：①建立层次结构模型；②构造判断矩阵；③一致性检验及计算权重；④层次总排序[17]。

1.2 熵权法确定客观权重

熵最早运用在物理学中，表示物质热状态的概率，是表征物质系统状态的函数。后来熵被用在信息论中，表示事物的不确定性，并将熵作为不确定性的度量，因此产生了信息熵，即一个系统越有序，信息熵越低，反之越高。现在很多专家以及学者将信息熵广泛应用于管理科学、生物医学、人工智能、金融学，评价决策等领域[18]。熵权法是一种客观赋值的方法，将其用到评价方面，用熵权表示某个评价指标的相对重要程度，当评价指标差异越大，信息熵越小，提供信息越多，权重越大，在综合评价中的作用越大；反之，当评价指标差异越小，信息熵越大，提供信息越少，权重越小，在综合评价中的作用就越小[19]。因此，在对评价对象的分析过程中，可以根据评价指标的差异度，利用熵权法计算各个指标的熵权，从而确定各指标的权重。具体步骤如下所述[20]。

1) 计算指标规范值yij，见式(1)。

(1)

式中：yij为规范值；xij为指标值。

2) 计算指标熵值ej，见式(2)。

(2)

式中：ej为指标熵值；k=1/lnm;yij为规范值。

3) 计算指标熵权wj，见式(3)。

(3)

1.3 确定变权综合权重

层次分析法是属于主观赋权的方法，在很大程度上受到研究人员经验、能力、知识水平的限制，容易导致评价结果与实际产生偏差，往往具有过度的主观色彩。而用熵权法求得的指标权重的大小是根据各指标的信息差异程度，得到的结果比较客观，尽量避免了评价人的主观因素对评价指标权重的影响。但是这两种方法确定的指标权重值一般是固定不变的，不会随着对象的改变而改变，即通常人们在做决策时会不自觉的遵循“均衡”原则[21]，也就是某个方案由于某个指标权重过大或者过小就会导致整个方案被放弃了，不能反应样本复杂的系统的非线性特征。为了做出更加正确合理的决策，本文引入了一种均衡函数，通过分别对层次分析法和熵权法得到的权重进行自动调整，从而体现决策者对评价对象的偏好，最后得出新的权重。同时为了使得到的数据更能反应实际情况，需要通过一定的运算整合，将层次分析法得到的权重和熵权法得到的权重进一步处理，步骤如下所述。

1) 设得到的指标权重表达式见式(4)。

(4)

式中，wj0为指标初始权重值。

2) 根据文献[21]提供的均衡函数进行计算，见式(5)。

(5)

3) 根据变权公式进行计算，得到变权权重wj，见式(6)。

(6)

式中，a为参数。

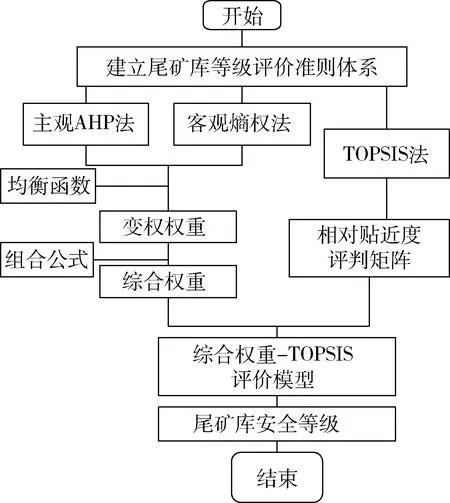
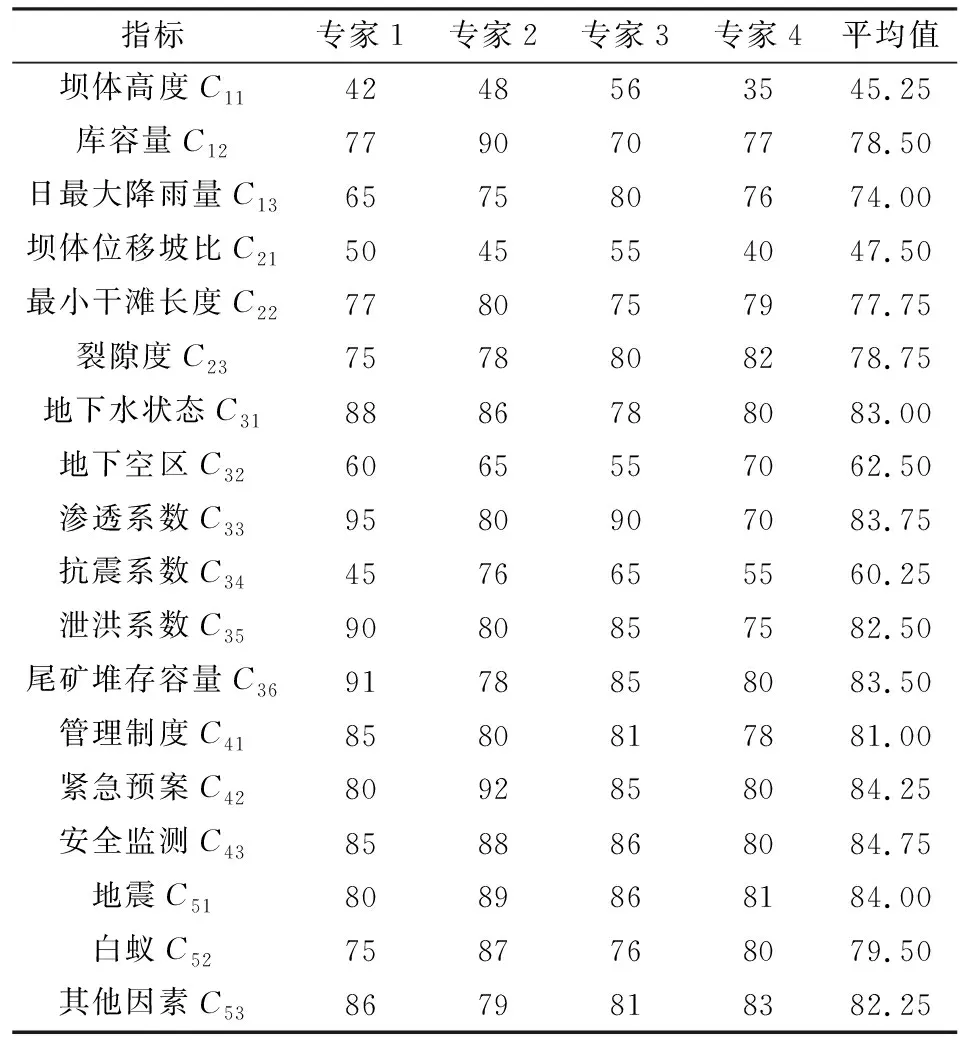
0

4) 将所得指标权重进行再次分配，见式(7)。

wj=εwαj+(1-ε)wβj

(7)

式中：wαj为AHP综合变权权重；wβj为熵权综合变权权重;ε为折中系数，ε越大，表示层次分析法确定的变权权重对综合权重的影响更大；反之，熵权法确定的权重值对综合权重的影响更大。通常情况下ε=0.5，重要性相当。虽然ε的取值依然带有一定的主观性，但是相较于直接用层次分析法或者熵权法得到的权重更加适合实际应用。

1.4 计算评价结果

本文采用综合变权-TOPSIS模型来计算评价结果。TOPSIS(technique for order preference by similarity to ideal solution)为接近理想点法，是一种多目标决策方法。该方法的基本思路是定义评判对象的理想解和负理想解，然后在可行的方案中找出一个方案，使得此方案距离理想解最近，同时又与负理想解距离最远。TOPSIS法引进相对接近度的概念来考虑正负理想解距离。理想解是各个指标达到最优，负理想解是各个指标均为最差[22]。

由TOPSIS法得到各指标的相对贴近度后，与准则层指标权重结合构造判断矩阵，最终得到评判对象，综合评价结果见式(8)。

Q=W×C

(8)

式中：C为贴近度评判矩阵；W为准则层权重。

根据上述变权综合权重和TOPSIS法的计算原理，将其用于尾矿库的安全评价，得到的计算流程见图1。

图1 计算流程图Fig.1 Calculation flow chart

2 实 例

2.1 工程简介

湖南省黄金洞尾矿库位于湖南省平江县黄金洞乡境内，是一个具有400多年开采历史的老矿山，目前生产规模是600 t/d。尾矿库库区山势陡峭，沟谷发育，地形起伏大，主沟发育有数条冲沟，尾部坡降较大，常年流水不断。库区沟谷大多呈“V”字型沟谷，山坡一般在35～50°之间，局部达到65°。该库区属于亚热带湿润季风气候，年降雨天数为150～182天，雨期在4～7月，秋季常干旱。该尾矿库占地面积300亩[注]1亩=666.67 m2。，主要为山地，是一个人为的具有高位能的泥石流形成区，存在安全隐患。

为了保证尾矿库系统的本质安全,要从客观物体因素和主观人为因素方面着手。大多尾矿库发生事故的原因一方面来自自身因素即构造缺陷，环境复杂；另一方面来自外界因素即设计不当，由人类行为造成。本文结合黄金洞尾矿库的实际情况，将导致尾矿库事故的指标进行组合与筛选之后，最终选择洪水漫顶、坝体溃坝、地基沉陷、安全管理和自然因素这5个方面作为目标层指标，选择坝体高度、库容量等18个方面作为措施层指标，建立黄金洞尾矿库安全评价指标体系，见图2。

在尾矿库的安全标准化管理范围内，按照尾矿库的安全标准化法律法规及技术规范，参照《金属非金属矿山安全标准化规范》《金属非金属矿山安全标准化规范尾矿库实施指南》《尾矿库安全技术规程》等文件和相关文献，将尾矿库的安全状态划分为四个等级:安全、较安全、较不安全、不安全，见表1。给相关专家及技术人员发送E-mail或者调查问卷表，专家根据尾矿库的实际情况，以专业知识和多年经验，以各个指标对整体体系的贡献度大小为基础来打分，打分值越高越好。其中,不安全对应区间(0～25分);较不安全对应区间(25～50分);较安全对应区间(50～75分);安全对应区间(75～100分)。最终得到每个指标的专家打分值，见表2。

图2 黄金洞尾矿库安全评价指标体系Fig.2 Gold cave tailings mine safety evaluation index system

表1 指标分级标准Table 1 Index grading standards

表2 专家打分表Table 2 Expert score table

2.2 确定综合权重

本文邀请了4位专家及技术人员对各指标进行打分和比较，运用MATLAB软件分别计算出各个指标在层次分析法和熵权法下的初始权重值。为了达到指标间的“均衡”原则，进一步将层次分析法和熵权法得到的权重值进行变权计算。根据式(6)中a的取值不同，可以将决策者分为悲观派、保守派、乐观派，即a分别取值为0.3、0.5、0.8，并通过计算最终得到不同情况下的的变权权重。最后为了避免层次分析法权重的主观性，以及熵权法权重的客观性，将两种方法得到的变权权重进行加权求平均，得到综合权重值，见表3。

2.3 确定安全等级

将表3得到的权重值分别与TOPSIS结合进行计算，由MATLAB软件计算得出的结果见表4。据表4计算结果可知AHP-TOPSIS模型(0.5560)和熵权-TOPSIS模型(0.5654)得出尾矿库安全状态属于较不安全等级；综合权重-TOPSIS模型得出尾矿库安全状态属于较安全等级。通过调查与核实，此尾矿库实际运行状况是在属于较安全状态。这表明在对尾矿库进行分析时，单纯使用AHP或者熵权法会因为人们主观认识差异或决策因素的片面性导致决策失误，与现实状况不符。综合变权指标权重根据实际情况发生变化，且通过对AHP和熵权法权重进行自动调整与处理，得到科学准确的权重值，为评价阶段打下良好基础。

由综合变权-TOPSIS模型得到的尾矿库安全状态虽然都属于较安全状态，但是a的取值不同，尾矿库得分也不同。当a=0.3时(0.6037)，决策者属于悲观派，做决策时对不利因素考虑较多，办事略悲观；当a=0.5时(0.7287)，决策者属于保守派，做决策时综合考虑不利和有利因素，考虑问题全面；当a=0.8时(0.6235)，决策者属于乐观派，做决策时对有利因素考虑的较多，办事较乐观。从得分情况来看，保守派得分最高，结果也最好，这也验证了在考虑变权时，大多数人将a取0.5。

表3 变权综合权重Table 3 Variable weight comprehensive weight

表4 安全等级Table 4 Security level

3 结 论

1) 通过对黄金洞尾矿库的实际调研，以及阅读相关文献，最终选取洪水漫顶、坝体溃坝、地基沉陷、安全管理、自然因素这五个准则层指标和坝体高度、库容量等18个措施层指标建立黄金洞尾矿库安全评价指标体系，通过分析得到此尾矿库安全状态属于较安全等级，符合实际情况。

2) 在确定指标权重时，本文通过构造均衡函数，引入变权综合。变权的目的是指标权重随着状态值的变化而变化，从而能更好地在决策中发挥作用。通过变权综合确定权重值相对于在决策中的常权不变更加具有科学性。虽然是变权综合，但是变权权重是在常权的基础上进一步求得的，也与常权有关，常权越大，影响越大，这符合生活常识。

3) 为了避免层次分析法确定权重时偏主观性和熵权法确定权重时偏客观性，本文引入了偏好系数，最终得到各指标的变权综合权重值。结合风险评估得出该尾矿库的安全度属于较安全区间。其中在措施层，坝体高度、抗震系数和安全管理三个指标的权重值较大，即对尾矿库安全运行的影响程度也最大。因此在对尾矿库安全监管过程中要适当控制坝体高度，使其保持在安全坝高的范围内；抗震系数虽与尾矿库所处地理位置及地下水文地质有关，但仍可以通过坝体建筑物的材料以及有效的安全管理来提高其抗震强度；在安全管理制度方面更要认真贯彻“安全第一、预防为主、防重于抢、有备无患”的方针。同时也要关注其他指标对尾矿库安全运行的影响，及时对尾矿库的整体与具体运行情况做出调整。

4) 尾矿库的安全评价具有综合性、复杂性、系统性的特点，在评价时需要尽可能地考虑全方面的评价指标，减少主观因素的影响，做到评价结果科学性、客观性。变权综合权重风险评估模型能够有效地得出尾矿库的安全度，计算简单，其评价结果可以作为决策时的理论依据，为尾矿库的安全评价提供了一种新的权重计算模型。