短型热电偶导热误差影响因素数值仿真分析
2019-01-18莫建伟荆卓寅李龙飞
莫建伟,荆卓寅, 李 彤,王 勇,李龙飞
(1.西安航天动力研究所,陕西 西安 710100;2.中国长城计量测试技术研究所,北京 100095)
0 引言
在先进航空航天发动机技术的研究中,经常会遇到高温、高速气流温度测试问题[1]。例如:在液体火箭发动机热试车中,温度参数的准确测量对于衡量发动机的性能是至关重要的。由于热电偶测温方法具有造价低廉、使用方便等特点,目前在工程上广泛采用,然而测温热电偶通常工作在高温、高压、高速流动环境下,热电偶与燃气、周围冷壁存在辐射换热,并且沿偶丝向热电偶壳体存在热传导损失,电偶的指示值是热电偶接点与周围环境换热形成的热平衡温度,并非测点处燃气的真实温度[2-5]。通常高温测量误差包含辐射误差、导热误差以及速度误差等,辐射误差相对于导热误差而言所占份额较大,在研究过程中一般采用忽略导热误差的方法以简化计算[6-10]。然而在火箭发动机的温度测量过程中,由于测温传感器强度等因素的限制,传感器深入流道内的尺寸很短,这样会产生很大的导热误差,而准确评估导热误差的大小对发动机的性能测量以及发动机工作状态的判定具有非常重要的意义。
针对这一情况,本文专门开展了温度传感器导热误差的数值仿真分析,研究在发动机实际气流速度条件下,温度传感器长径比以及支座温度对导热误差的影响,获得发动机实际工况条件下短型热电偶温度传感器导热修正系数,提高测量准确度。
1 数值仿真方法及准确性分析
1.1 数值仿真方法
短型热电偶采用铠装结构,热电偶在流道安装简化模型如图1所示,为了消除辐射误差的影响,流道壁温设定与气流温度一致,流道壁厚2 mm。采用Ansys软件进行数值模拟,选用RNGκ-ε湍流模型,标准壁面函数法,二阶迎风格式、耦合隐式求解,气流通道内的速度和温度壁面条件分别取壁面无滑移、等温边界条件。气流通道分别取压力进口和压力出口,冷却壁处温度设置为测温传感器的冷端温度。流体区域和热电偶壳体固体区域采用热固耦合。

图1 短型热电偶安装简化模型Fig.1 Sketch of short type thermocouple installation model
1.2 数值仿真方法准确性分析
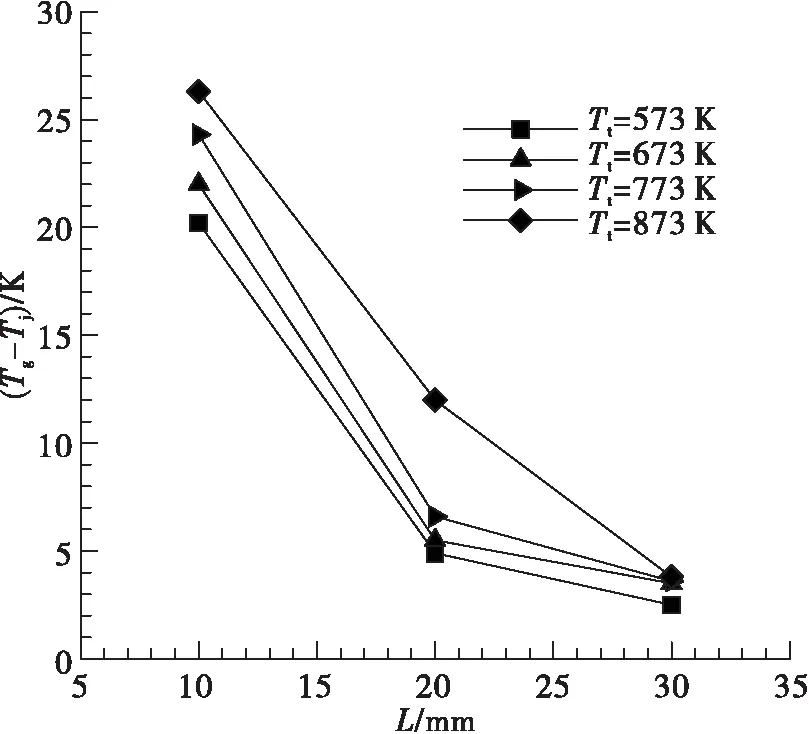
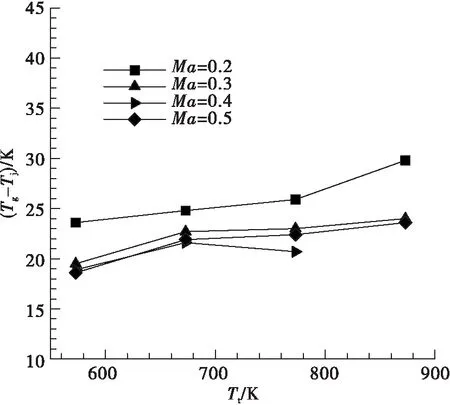
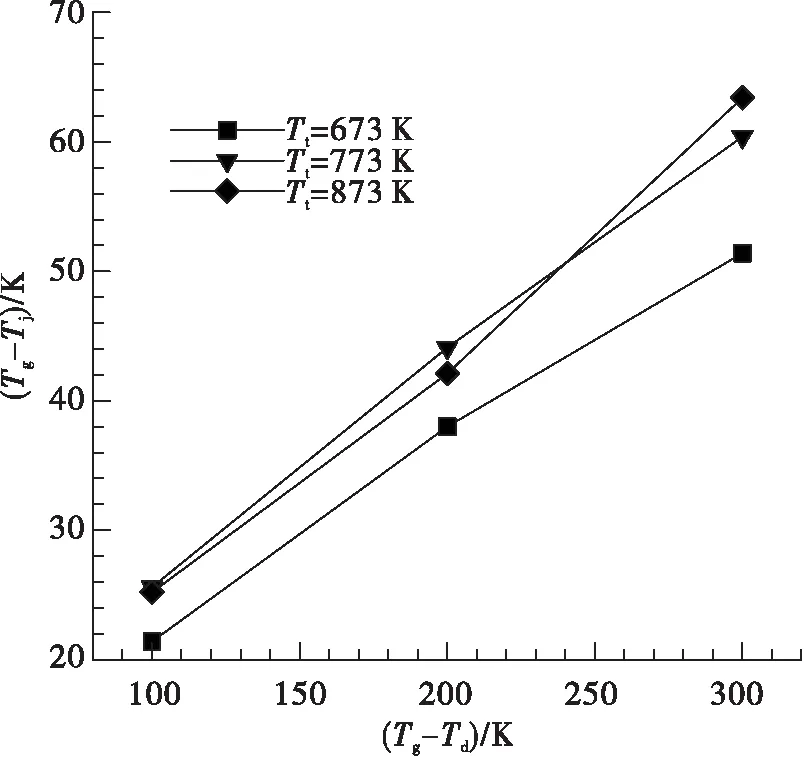
为了验证数值仿真的准确性和可靠性,根据NACA研究报告中提供的气流绕流热电偶丝的导热误差相关试验数据[2,11],在相同工况下采用Ansys软件进行仿真计算,并与文献[2]中的导热误差修正系数对比来验证仿真结果的准确性。图2为文献[2]中的气流绕流热电偶丝示意图,热电偶丝总长为L,L/2处为热电偶接点,基座处温度为Tb,基座处温度小于气流温度Tb 由表1中参数可得气流雷诺数Re=3 690,由文献[2]中努赛尔数的计算方式: 式中:Re为雷诺数;Pr为普朗特数。 可得:Nu=24.8 从而有:h=Nuλ/d=917 W/(m2·K) 文献[2]中给出热电偶丝在此工况下的导热误差修正系数约为H=0.16。 图2 气流绕流热电偶丝Fig.2 Airflow passes around thermocouple wire ρ/(kg·m-3)V/(m·s-1)Tt/Kd/mL/mPr0.417164.78500.0020.020.59 为了校验数值仿真的准确性,建立了气流绕热电偶丝的几何模型,并采用Ansys软件进行相同工况下的导热误差仿真计算[12]。 根据数值计算可得热电偶表面平均换热系数为: 式中:Q为热电偶丝向外部导热量;A为电偶丝表面积;ΔT为流体与热电偶丝的平均温差。这与从文献[2]中得到的换热系数917 W/(m2·K)非常接近。 另外提取仿真结果中热电偶丝接点处的温度可得导热误差修正系数: 这与文献[2]中查到此工况下的导热修正系数0.16非常一致。 上述计算结果表明,无论是热电偶丝表面平均换热系数还是热电偶丝导热误差修正系数,仿真结果与文献[2]中的结果都非常一致,这也验证了数值仿真的准确性。 热电偶导热误差理论估算公式如[13]: 式中:Tg为气流总温;Tj为热电偶温度示值;Td为支座温度;α为热电偶端与流体的对流换热系数;L为传感器插入深度;d为传感器直径。 对于特定的热电偶,λ和d已经确定,在测量中影响导热误差的主要因素有热电偶插入深度、对流换热系数和支座温度,而对流换热系数主要受来流总温和速度影响。下面将通过数值仿真分别研究热电偶插入深度、来流总温、来流马赫数以及基座温度对热电偶导热误差的影响。 来流马赫数为0.3,来流总温分别为573 K,673 K,773 K,873 K,在此条件下分别研究热电偶插入深度30 mm,20 mm和10 mm情况下导热误差的变化。 图3给出了不同来流总温条件下热电偶导热误差随插入深度的变化,可以看出,当热电偶插入深度为30 mm时,热电偶导热误差约为4 K。随着热电偶插入深度的减小到20 mm,导热误差增加到7K左右,但当热电偶插入深度减小到10 mm时,导热误差迅速增大到20~30 K,这主要是由于热电偶插入深度较短时,热电偶导热热阻减小使得导热误差增大[14]。 图4为不同来流马赫数情况下导热误差随总温的变化趋势,可以看到,不同的来流马赫数情况下导热误差都表现出随总温升高而增大的趋势,这是由于总温升高后,热电偶壳体导热率增加使得导热热阻降低,导热误差增大。在同一总温下,导热误差表现出随马赫数增大而减小的趋势,这是由于随着马赫数的增大,气流的特征雷诺数增大,从而使气体与热电偶的对流换热系数增大,由导热误差理论估算公式[13]可知,热电偶导热误差减小。 图3 不同总温下导热误差随插入深度的变化Fig.3 Variation of thermal conductivity error with insertion depth at different total temperatures 图4 不同马赫下导热误差随总温变化关系Fig.4 Variation of thermal conductivity error with total temperature at different Mach 图5为不同总温下热电偶导热误差随Tg-Td的变化关系,其中Tg-Td为气流总温与基底温度的差值,Tg-Td越大表示基底温度越低。从图5中可以看出,在不同的来流总温情况下,热电偶导热误差随Tg-Td增大而增大,相同的Tg-Td情况下,气流总温越低热电偶导热误差越小。 图5 不同总温下热电偶导热误差随基底温度的变化Fig.5 Variation of thermocouple conduction error with substrate temperature at different total temperature 从以上热电偶导热误差的仿真结果中可以看到,不同热电偶插入深度、气流马赫数、气流总温以及基底温度都会对热电偶导热误差产生影响。为了综合分析各因素对导热误差修正系数的影响程度,根据上述计算中不同工况下导热误差的结果,建立导热误差修正系数与热电偶插入深度、气流总温、气流马赫数和基底温度的响应面模型。 假设导热误差修正系数模型为二阶响应面模型,并且不考虑交叉项的影响。影响导热误差修正系数的因素分别为热电偶插入深度L,气流马赫数Ma,气流总温Tt以及总温与基底的温差Tg-Td,则导热误差修正系数响应面模型的数学表达式为: H=β0+β1L+β2Ma+β3Tt+β4(Tg-Td)+ β5L2+β6Ma2+β7Tt2+β8(Tg-Td)2 上式中共有9个未知数,分别为β0…β8,根据上述计算结果拟合可得: β=[0.571 3,-0.036 97,-0.684 5,0.000 197 3,-0.000 382 7,0.000 680 8,0.783 8,-2.913 3×10-8,4.173 7×10-7] 图6为拟合得到的导热误差修正系数与各因素之间的关系,其中实线表示拟合曲线,而虚线为置信区间,可以看到,热电偶插入深度对导热误差影响最大,插入深度较小时,导热误差很大,随着热电偶插入深度增加,导热误差迅速减小并趋于一个很小的值,此情况下可认为导热误差为零,因此在实际测量中应选择合适的热电偶插入深度,减小测量误差。导热误差修正系数随气流马赫数增大而减小,但其变化幅度较小并随马赫数增大而逐渐趋于平缓。导热误差修正系数随气流总温增加呈现近似线性增加,而导热误差随Tg-Td的增大呈现近似线性的减小,气流温度变化对误差的影响主要原因是温度变化造成了热电偶壳体平均热导率的变化,从而使导热热阻发生变化。 为了评估获得的导热误差修正系数响应面模型的准确性,表2是不同工况下响应面模型的计算值和真实值的比较,其中Hrsm是响应面模型的计算值,H为相同工况下的真实值,可以看到,二者之间差别非常小,这说明建立的导热误差响应面模型是准确可信的。 图6 导热误差修正系数与各影响因素之间的关系Fig.6 Relationship between thermal conductivity error correction coefficient and various influencing factors 序号L/mmMaTt/K(Tg-Td)/KHHrsm△/%1100.3574.9101.90.1980.2040.6%2100.3876.3103.30.2540.2500.4%3200.3579.1107.20.0460.0370.9%4100.5878.2100.20.2350.2400.5%5100.3875.3302.30.2090.2070.2% 建立了短型热电偶温度传感器导热误差仿真模型,通过与国内数据对比验证了仿真模型的准确性。接着通过仿真计算,研究了不同热电偶插入深度、不同来流马赫数、不同来流总温和不同基底温度对导热误差修正系数的影响规律,并建立了导热误差修正系数的响应面模型。主要有以下结论: 1)在热电偶导热误差影响因素中,插入深度影响最大。热电偶导热误差随插入深度减小迅速增大,当热电偶插入深度为30 mm时,热电偶导热误差约为4 K。但当热电偶插入深度减小到10 mm时,导热误差迅速增大到20~30 K。 2)相同的来流马赫数情况下,导热误差随总温升高而增大,这是由于总温升高后,热电偶壳体导热率增加使得导热热阻降低,导热误差增大。在同一总温下,导热误差表现出随马赫数增大而减小的趋势,这是由于随着马赫数的增大,气流的特征雷诺数增大,从而使气体与热电偶的对流换热系数增大,热电偶导热误差减小。 3)导热误差修正系数随Tg-Td的增大而减小,这种变化趋势主要原因是当Tg-Td增大时,Td变小使得热电偶壳体的平均热导率降低,导热热阻增加,从而使导热误差修正系数减小。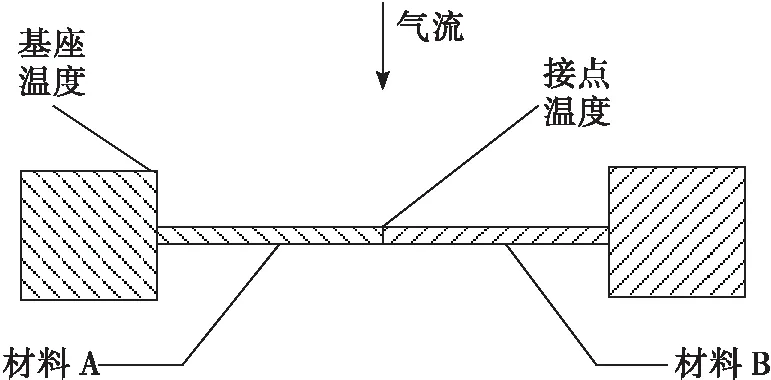

2 数值模拟结果分析
2.1 热电偶插入深度对导热误差的影响
2.2 不同工况对热电偶导热误差的影响研究
2.3 不同基底温度对热电偶导热误差的影响研究
2.4 导热误差修正系数数学模型


3 结论
