表贴式永磁电机转子偏心故障快速诊断研究

李全峰 黄厚佳 黄苏融 李琳红

摘要：针对表贴式永磁同步电动机运行时转子发生偏心故障问题，提出一种利用振动速度频谱分析来快速诊断的新方法。首先，运用解析法推导出转子未偏心时径向电磁力波表达式，在此基础上通过引入静偏心修正系数ε（θ）和动偏心修正系数εd（θ），进一步推导出转子静偏心和动偏心时径向电磁力波解析表达式。通过解析分析表明：当转子静偏心时会新增阶数为（r±1），频率为kf1的电磁力波分量;而转子动偏心时会新增阶数为（r±1），频率为（k±1/p）f1的电磁力波分量。其次，运用有限元法通过两台表贴式永磁电机实例验证了解析分析结果。最后，通过无线振动测试实验来验证运用该振动速度频谱分析法快速诊断电机转子发生偏心故障的可行性。

关键词：表贴式永磁同步电动机;偏心故障诊断;径向电磁力波;振动速度频谱;有限元仿真

中图分类号：TM351

Abstract：A novel method is addressed to fast diagnosethe problem of surface-mounted permanent magnet synchronousmotors（SPMSM） rotor eccentricity fault by using the analysis of the frequency spectrum of vibration velocity. Firstly， the radial electromagnetic force waves（REFW） expression was deduced by the analytical method when the rotor is normal. Based on above results， both static and dynamic eccentricity correction coefficient， ε（θ） and εd（θ）， were introduced to deduce the REFW expression when the rotor is static and dynamic eccentricity. It finds out by the analytical results that when the rotor is static eccentricity， and it is newly produced of REFWs component with order of （r±1） and frequency of k f1， while when the rotor is dynamic eccentricity， it is newly produced of REFWs componentwith order of （r±1） and frequency of （k±1/p）f1. Secondly， the finite element method（FEM）was used to verify the correctness of analytical results by the two SPMSM as examples. Finally， the feasibility of using the method of the vibration velocity spectral analysis forfast diagnosing the problem of rotor eccentricity fault was validated by the wireless vibration test.

Key words：surface-mounted permanent magnet synchronousmotors;diagnosis of eccentricity fault; refw; vibration velocity spectrum; finite element stimulation

0 引言

表贴式永磁同步电动机因其具有良好的机械特性、伺服特性和高效率在工业界中被广泛应用 [1]。但在电机制造过程中以及电机运行承受剧烈载荷时，很容易造成电机定转子轴线不对中而出现转子偏心，从而造成气隙分布不均匀，使电机运行时产生较大的电磁振动，严重影响电机的性能和使用寿命。因此，针对表贴式永磁电机转子偏心故障机理及快速诊断技术的研究十分必要。

七八十年代早期，國内外学者主要对电机偏心故障引起气隙磁导的变化机理进行了深入研究，奠定了理论分析基础。1974年苏联学者舒波夫分析了异步电机气隙偏心对电磁噪声的影响，指出偏心会使某些交流电机有时在个别频谱成分中出现较高的噪声级，给出了电机静态和动态偏心下的气隙磁导公式，指出偏心时会产生附加磁场，其气隙磁密幅值正比于相对偏心率的一半;并举例说明一台500千瓦4极异步电动机，当偏心值为0.1时，其法向电磁振动为78分贝[2]。1977年捷克斯洛伐克科学院教授B.Heller和V.HAMATA博士指出转子偏心会在气隙中产生新的谐波，这些谐波与具有相同阶次但不同频率的其他谐波干涉产生一个合成谐波时，会造成零阶振动;同时指出转轴上转子的偏心会造成引起噪声的单边磁拉力[3]。Cameron、Thomson和Dow的研究表明气隙偏心将导致气隙圆周方向的磁导不均匀分布，进而造成气隙磁场的不对称分布，进而在定子电流中会以谐波反映出，证明了气隙偏心特征的定子电流频谱，并给出了频谱成分分量的频率，表明气隙偏心频率成分的分布是从低频到高频都存在的，具体取决于电机的设计和结构参数[4]。

国内的陈永校和诸自强教授等在八十年代较早研究了电机偏心故障对电机电磁振动噪声的影响，给出了偏心时产生的磁导波，指出当偏心时会产生振动频率与转差率有关的拍频振动[5]。

九十年代到二十一世纪初，国内外学者针对电机偏心的研究主要集中在产生的不平衡电磁力特性方面。学者SmithAC等在文献[6-9]中针对感应电动机，研究了转子偏心时所产生的不平衡磁拉力，运用解析法推导出转子偏心时不平衡磁拉力计算公式，并进行了相关实验验证，但由于感应电机与表贴式永磁电机在结构上存在较大的差异，因此研究结论并不适用于表贴式永磁电机。文献[10]研究了水利发电机转子偏心时磁路饱和对不平衡磁拉力的影响，研究表明转子偏心会进一步加剧不平衡磁拉力，使电机产生更大的振动。学者Dimitri Torregrossa在文献[11]中通过场重建法（FRM）在永磁同步电机部分退磁和转子静偏心的情况下对电机转矩脉动和振动噪声进行深入研究，文中将场重建法所得的结果与有限元法和实验法所得的结果进行对比，验证了该方法的可行性，然后分别对部分退磁和转子偏心时电机的径向、切向电磁力，转矩脉动的状况进行深入分析，通过与电机正常运行时对比，指出永磁同步电机部分去磁和转子静偏心使电机运行时转矩脉动和振动噪声大大增加，转子静偏心的作用尤为明显。文献[12]运用等效剩磁法对永磁电动机转子偏心时的磁场进行计算，对转子偏心时磁密谐波特性进行了分析，将解析模型与有限元模型结果对比，验证了所提方法的准确性，该研究为下步分析转子偏心时径向电磁力波和电磁振动特性奠定了一定的理论基础。文献[13-14]运用解析分析法对转子未偏心时永磁同步电机径向电磁力波表达式进行了详细推导，得到电机空载和负载运行时的径向电磁力波幅值、频率及空间阶次特性。文献[15-17]从分析径向电磁力波入手，对电机振动噪声特性进行研究，找出了对电机振动噪声影响较大的分量，分析了电机相关设计参数对电机电磁振动噪声的影响，提出了准确预测电机电磁振动噪声的方法并通过相关实验进行了验证。

近年来，随着工业4.0以及未来智能工厂概念的提出，对转子偏心故障的研究主要集中在振动监控和故障诊断技术方面。2015年国外学者Ilhan Ayd?n等人提出了运用多传感器对感应电机的温度、振动、电流等进行无线检测并根据检测结果对判断电机是否正常运行[18]。ABB公司在2017年推出了电机智能监测系统ABB AbilityTMSmart Sensor新产品，通过在电机机壳侧面安置的无线蓝牙智能传感器实时监测电机运行状态，包括电机运行时X轴、Y轴和Z轴的振动位移、速度和加速度情况，以及电机温升等参数，并将这些数据上传至云端进行后台处理，最后判断出电机当前运行是否正常，但目前该产品还处于市场初級阶段，且只针对低压小功率异步电动机。

目前，电机无线监控智能故障诊断技术主要针对电机运行的“健康”状况进行无线监控，对其振动、噪声、温度和湿度等运行参数信号进行实时采集，并通过接收设备传送到云端，由后台下载数据后通过智能诊断系统对数据进行综合分析，从而判断电机的综合运行状况，预测电机使用寿命。其中对电机运行时各位置振动状态的实时判断是该智能故障诊断技术的核心。因此，如何能够快速的诊断电机适时运行状态十分重要。

综上所述，关于电机转子偏心故障问题的研究主要集中在产生的气隙磁导、不平衡磁拉力以及气隙磁场的分析，且多数研究集中在感应电机，对永磁电机偏心的研究相对较少，而且大部分为解析法推导和有限元验证，并没有通过具体的偏心实验来验证。而对表贴式永磁电机，更是缺乏一套行之有效的偏心故障快速诊断方法来判断电机运行时的可靠性，因此缺乏一定的工程实践性。

在前人研究工作的基础上，本文提出了一种通过无线振动测试系统实时监测振动频谱信号来判断表贴式永磁同步电机是否出现偏心故障的快速诊断方法。首先运用解析分析法比较转子静态偏心和动态偏心时径向电磁力波与转子未偏心时的差异，从理论分析中找到转子静、动态偏心时新增的径向电磁力波阶次与频率，作为判断转子静、动态偏心的重要理论依据;其次，通过两台电机实例利用有限元仿真验证解析分析的正确性;最后通过无线振动测试实验，对比转子正常和偏心状态运行时的振动速度频谱，从而进一步验证该转子偏心故障快速诊断方法在实际工程中的应用。

1 转子偏心解析分析

首先从气隙磁密出发，运用解析法分别推导出转子正常、静态偏心和动态偏心时新增径向电磁力波解析表达式，找出偏心时新增的电磁力波阶次和频率，为偏心振动故障的快速诊断方法提供必要的理论依据。为方便说明，本文中以2pτ为基准波长，p为电机极对数，τ为极距。

1.2转子偏心时径向气隙磁密

转子偏心分静态偏心和动态偏心两种情况。当转子旋转中心与定子中心轴线不重合，转子各机械角对应的气隙长度不随转子旋转而变化，此时转子为静偏心，如图1中a图所示。例如在装配过程中转子转轴几何中心与定子铁芯几何中心线不重合时会出现静偏心。

当转子旋转中心轴线与定子中心轴线重合但与转子静止时的中心轴线不重合时，即气隙不同位置气隙大小随着转子旋转而改变时，转子为动态偏心，此时不同机械角对应的气隙长度随时间而变化，如图1中b图所示。例如在转子铁芯加工过程中内外圆不同心或者电机受到冲击导致轴发生弯曲变形等因素造成转子动偏心。

根据上述解析推导，利用MATLAB编写电机偏心和未偏心时的径向电磁力波解析计算程序，以一台额定功率4.2kW表贴式永磁同步电机为例，电机相关参数如表3所示。对其静态偏心和动态偏心下径向电磁力波进行解析计算，并与未偏心时的径向电磁力进行对比。使转子偏心距分别为气隙的30%和60%，计算转子静偏心和动偏心时力波的空间阶次分布和频率分布，并将计算结果与转子未偏心时对比。

图3、4分别为偏心距为气隙长度的30%和60%时转子静偏心和动态偏心下力波的空间谐波分布和转子未偏心时的对比图。由解析分析可知，转子未偏心时，主要产生阶数为0和8的电磁力波。当转子发生偏心后，除了产生0阶和8阶径向电磁力波，还会产生1阶、7阶和9阶幅值较大的径向电磁力波，对应于解析分析中新增的阶数为（r±1）的径向电磁力波。以基波电流频率为基准频率，力波实际频率除以基准频率便得到力波的倍频数，如表3所示，静偏心时新增力波频率为kf1，则相应倍频数为k;同理，转子动偏心时新增力波倍频数为（k±1/p）。

由图中结果可以看出当转子静偏心时，1阶力波对应的频率为0Hz，尽管力波阶数低但不会引起振动，7阶和9阶力波对应的倍频数为2，因此转子静偏心后，二倍频振动分量会相应增大。转子动偏心时，1阶力波对应的倍频数为1/4，由于力波阶数较低，幅值较大，因此转子动偏心后1/4倍频的振动分量会明显增大，此外7阶和9阶力波对应的倍频数为7/4和9/4，因此转子动偏心后还会产生倍频数为7/4和9/4的振动分量。图中还可看出，无论转子发生动偏心或是静偏心，其产生的空间阶次和幅值是相等的。通过图3和图4对比可以看出偏心距越大，新增力波幅值也越大。

图5、6为偏心距分别为气隙的30%和60%时转子正常和不同偏心状态下的径向电磁力波的频域阶次分布。以电枢电流基波为基准，将电磁力波的频率折换成倍频数。由解析分析可知，转子不偏心时，主要产生倍频数0、2、4、6的径向电磁力波，当转子发生静偏心后，不会产生其他频率的电磁力波成分，但当转子发生动偏心时会新增倍频数为1/4、7/4和9/4等力波成分。

从上述解析计算结果可以看出该4.2kW表贴式永磁电机当转子发生静偏心时，会新增二倍频率力波分量，阶数小于未偏心时该频率所对应的力波阶数，因此转子静偏心时二倍频振动分量会有所增加;当转子发生动偏心时，会产生1阶1/4倍频、7阶7/4倍频和7阶9/4倍频的力波分量，因此会产生相应频率的振动分量。因此，根据上述分析结果，可以通过分析电机振动频谱特性对电机的偏心故障进行诊断。

2 转子偏心有限元仿真分析

为了验证上述解析分析的结论，以上述4.2kW永磁同步电机为例，在Maxwell 2D中建立有限元分析模型，对转子在静态偏心和动态偏心两种运行状态下进行仿真分析，其转子偏心60%下磁密云图如图7所示。

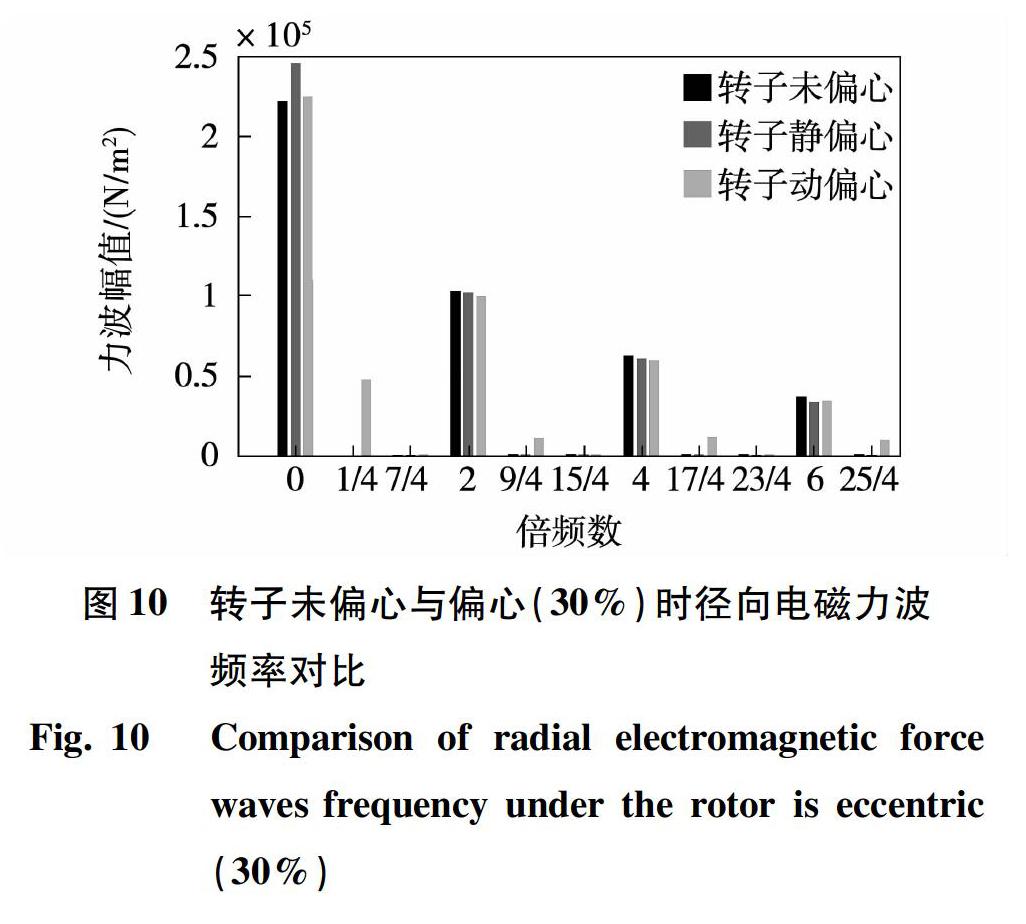
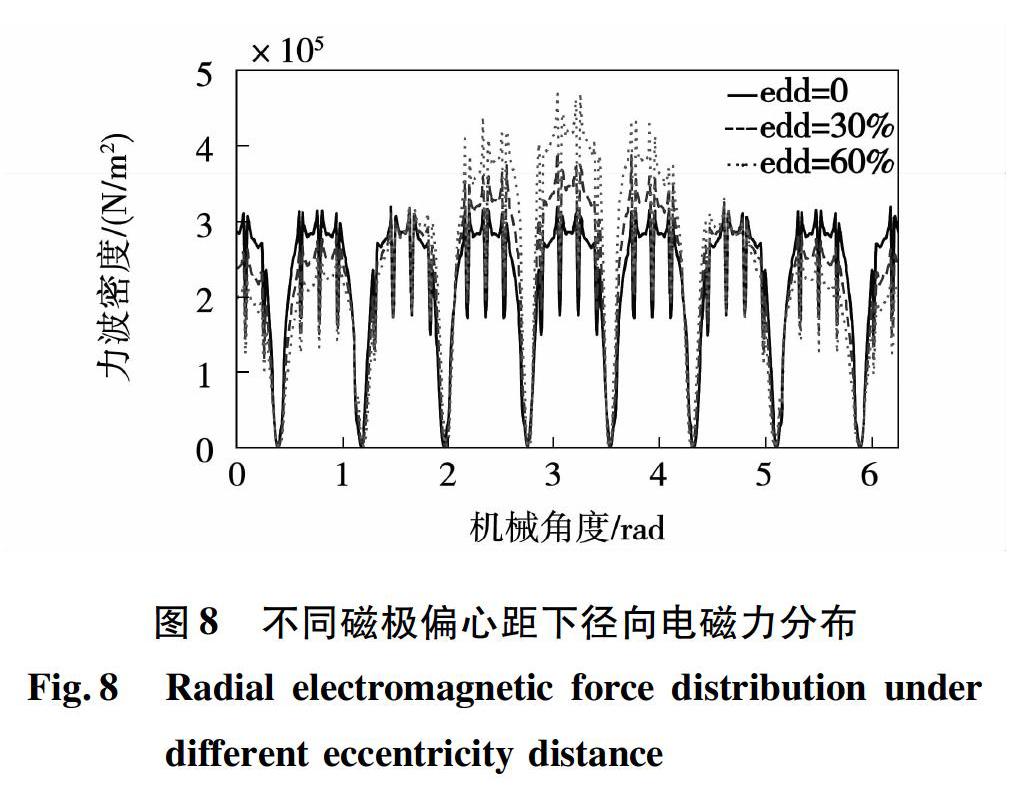
无论转子发生动偏心或静偏心，其力波空间阶次分布是不变的，为了与解析计算结果进行对比，在有限元仿真中分别计算偏心距为气隙的0%、30%和60%下径向电磁力波波形，计算结果如图8所示。

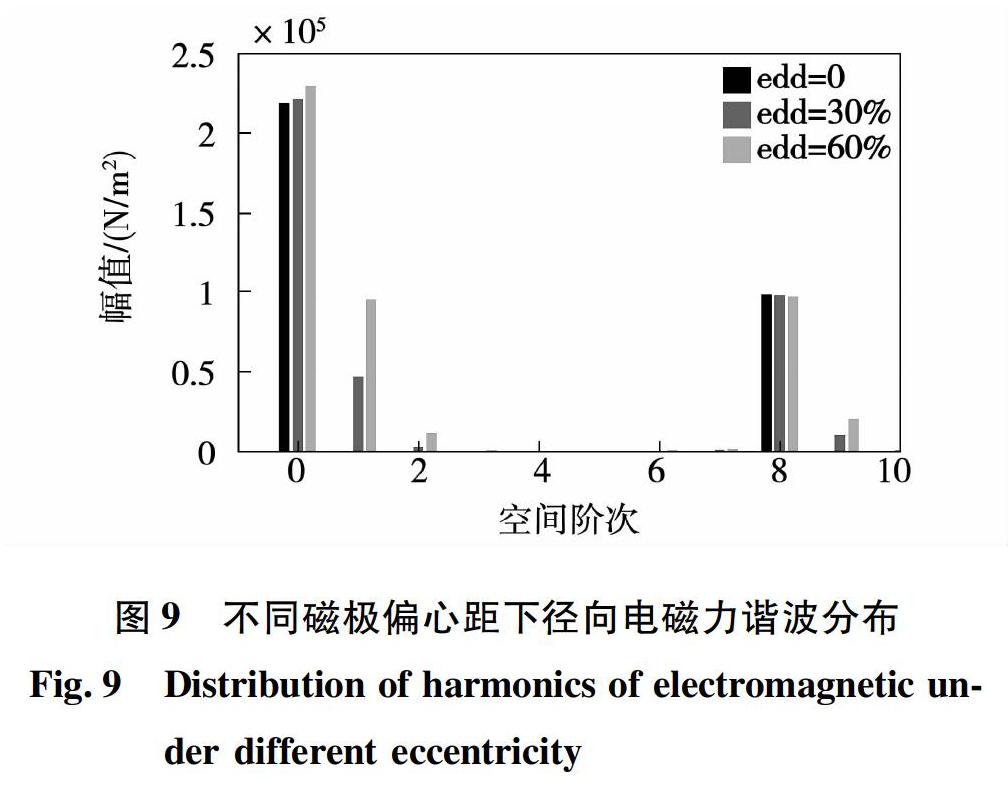
图中可以看出，当转子偏心后，径向电磁力波会发生相应的畸变，随着磁极偏心距的增大波形畸变越大。对所求波形做快速傅里叶变换得到力波空间阶次分布，如图9所示。从图9中可以看出，转子未偏心时，主要产生阶数为0和8的径向电磁力波，当转子偏心后，新增阶数为1、7和9的径向电磁力波，正好对应于阶次为（r±1）的力波分量。随着磁极偏心距的增大，新增力波幅值会相应的增大。

图9的有限元结果与图3、4的解析结果相比力波的幅值明顯降低，原因是解析计算时并未考虑铁芯饱和的影响，导致气隙减小位置处磁密大于实际磁密，因此有限元仿真和解析计算在力波幅值计算结果上存在一定的差异，但新增的力波阶数及频率是相同的。

将偏心距分别设置为气隙的30%、60%，计算不同偏心距下径向电磁力波频率分布并与转子未偏心时的频率分布进行对比，结果如图10和图11所示。从图10和图11中可以看出，转子静偏心时力波频率分布同转子未偏心时相同，但当转子发生动偏心时，会新增倍频数为1/4、7/4和9/4等力波成分。随着磁极偏心距的增大，新增力波幅值也相应的增大。

通过对电机进行偏心和未偏心时有限元仿真结果对比，发现转子偏心后会新增空间阶次为1、7、9的力波分量，当转子动偏心后还会新增倍频数为1/4、7/4、9/4的力波分量，进一步验证了解析分析结论，但由于解析分析中未考虑铁芯饱和的作用，因此有限元仿真和解析计算在力波幅值计算结果上存在一定差异。

为了进一步验证解析结论的通用性，以另一台70W 4极小型表贴式永磁电机为例，其基本参数如表4所示，偏心磁密分布如图12所示，运用有限元法对电机转子正常、静态偏心60%和动态偏心60%下的径向电磁力波进行空间分布和频率分布对比如图13和图14所示。

由图13可以看出，当转子正常时，电机径向电磁力波空间阶次主要为0、2、4、6、8，但当转子发生动态偏心或静态偏心时，新增空间阶次为1、3、5、7、9的径向电磁力波，对应于（r±1）阶径向电磁力波。

由图14可以看出，转子正常与发生静态偏心时，电机径向电磁力波倍频数主要为2、4、6，但转子发生动态偏心时会新增阶数为1/2、3/2、5/2、7/2、9/2、11/2、13/2，对应于倍频数为（k±1/p）的径向电磁力波。

通过上述两台表贴式永磁同步电动机有限元分析结果证实了前面解析法得出的可以通过分析电机振动频谱特性对电机偏心故障进行诊断的结论。

3 实验验证

为了验证解析分析和有限元仿真分析的正确性，采用无线故障诊断技术对振动速度进行测试，诊断流程图如图15所示。首先将工厂里的永磁同步电动机电机加装无线传感器;无线传感器将各电机的实时运行振动检测信号传给无线信号处理器;由无线信号处理器上传到云端数据存储平台;通过计算机对下载的云端数据进行后台故障诊断分析;最终将处理结果反馈给智能工厂中央处理器并由中央处理器对电机发出继续运行或停机维护的指令。

本文研究的4.2kW电机无线振动测试实验如图16所示。在被测电机机壳表面安装无线速度传感器，首先对转子正常时的运行状态进行振动速度测试，测得电机运行正常时机壳表面的径向振动速度，并通过自编的振动频谱分析程序自动识别电机振动速度的倍频数，然后再做偏心实验。由于模拟偏心难度较大，因此实验时采用将电机两边端盖儿外表面进行边缘打磨，使轴装配中心与定子中心发生偏离，由于偏心距太小试验结果不明显，偏心距太大安装较为困难，故本试验选取使电机主轴轴线与转子铁芯中心线偏心约为气隙的30%来模拟转子静态偏心。

为了模拟转子动态偏心运行，一般运用火焰矫正法使轴发生弯曲或运用线切割法使转子中心孔偏移一定的距离。火焰矫正法即使用乙炔火焰以不均匀加热的方式对转子轴的某一位置进行高温（600～800℃）加热，待冷却后会产生收缩变形，从而使转子发生椭圆变形，但此方法的关键是掌握火焰局部加热引起的变形规律，需控制温度和重复加热次数。由于该方法对工艺要求较高，因此，本文采用线切割使转子中心孔偏移的方法来实现转子动偏心。具体如图17所示，将转子轴中心孔偏移，使转子动偏心时的偏心距为气隙长度的30%。

图18为转子正常和发生静、动态偏心时速度随时间变化的波形图，从图中可以看出当转子偏心时振动速度明显偏大。对其进行快速傅里叶变换得到振动速度频谱图，如图19所示。

从图19中试验结果可以看出，当转子动偏心时电机整体振动水平要高于电机转子正常时的振动水平。由于电机极对数为4，因此产生的机械转频振动分量基频为1/4 f1，图中无论转子是否偏心都存在倍频数为1/4、3/4、6/4的振动分量，即为机械转频振动的1、3、6次分量。与转子正常振动速度频谱相比，转子偏心时后2倍频振动分量明显增大，说明转子发生静偏心，同时1/4倍频振动分量也显著增大，并且新增了9/4倍频振动分量，两者恰好对应于倍频数为（k±1/p）次电磁力波分量，说明转子发生动偏心。

综上所述，从解析推导和有限元分析中均发现当转子发生静偏心时虽然径向电磁力波频率不变，但较不偏心时幅值有所增加，可通过与正常状态下振动速度频谱幅值对比来判断是否发生静偏心故障;当发生动偏心时会新增倍频数为分数的电磁力波分量，而这些分量会产生较大的振动，因此可通过分析振动速度频谱中新增倍频数来诊断电机是否发生动偏心故障，具体归纳如表5所示。

4 结论

本文运用解析法推导出永磁同步电机转子偏心时的径向电磁力波解析表达式，得到转子静态偏心和动态偏心时径向电磁力波空间阶次和频率变化;并从径向电磁力波着手对转子偏心时永磁同步电机电磁振动特性进行研究，从而提出了一种利用振动速度频谱分析判断电机是否发生静、动态偏心故障的快速诊断方法。并分别通过有限元仿真和无线振动实验进行了验证，可得到结论：1） 当转子发生静偏心时在原有电磁力波基础上会新增空间阶次为（r±1）且频率不变的径向电磁力波分量，新增的同频低阶电磁力波会极大增加电机振动水平。2） 当转子发生动偏心时在原有电磁力波基础上会新增空间阶次为（r±1）且频率为（k±1/p）f1的电磁力波分量。3） 在电机故障诊断时，如果发现2倍频振动速度幅值明显偏大，则可判断为出现静偏心故障;如果检测系统诊断出现倍频数为（r±1/p）的振动速度信号时，则可判断电机出现动偏心故障。如果二者同时出现，则可判断电机既发生静态偏心故障又发生动态偏心故障。

参考文献

唐任远等著. 现代永磁电机理论与设计[M].北京：机械工业出版社，2015.

舒波夫（苏）.电机的噪声和振动[M].北京：机械工业出版社，1974.

B. Heller，V.HAMATA.HARMONIC FIELD EFFECTS IN INDUCTION MACHINES. Elsevier Scientific Pub. Co. 1977.

沈標正.电机故障诊断技术[M].北京：机械工业出版社，1996.

陈永校，诸自强，应善成.电机噪声的分析和控制[M].浙江：浙江大学出版社，1987.

SmithAC， Dorrell D G. Calculation  and measurement  of  unbalanced  magnetic  pull  in  cage induction  motors  with  eccentric  rotors.Part 1：analytical   model[J]. IEE Proc-Electr. Power Appl.， 1996， 143（3）： 193-201.

Dorrell D G， Smith A C. Calculation  and measurement  of  unbalanced magnetic  pull  in  cage induction  motors  with  eccentric  rotors.Part 2： experimental investigation[J]. IEE Proc-Electr. Power Appl.， 1996， 143（3）： 202-210.

Dorrel，D. G. Sources and characteristics of unbalanced magneric pull in three-phase cage induction motors with axial-varying rotor eccentricity[J].IEEE Transactions on Industry Applications，2011，47（1）：12-24.

S. Nandi，R. M. Bharadwaj，Hamid A. Toliyat. Performance analysis of a three-phase induction motor under mixed eccentricity condition[J]. IEEE Transactions on Industry Electronics， 2002，17（3）：392-399.

Richard Perers，Urban Lundin，Mats Leijon. Saturation effects on unbalanced magnetic pull in a hydroelectric generator with an eccentric rotor[J]. IEEE Transactions on Magnetics，2007，43（10）：143-149.

Dimitri Torregrossa， Amir Khoobroo， Babak Fahimi. Prediction of acoustic noise and torque pulsation inPM synchronous machines with static eccentricity and partial demagnetization using field reconstruction method[J]. IEEE Transactions on Industry Electronics， 2012，59（2） ：934-944.

张冉，王秀和，杨玉波，等.基于等效剩磁的永磁电动机转子偏心磁场解析计算[J].电工技术学报，2009，24（5）：7-12. Zhang Ran，Wang Xiuhe ，Yang Yubo ，Wang Daohan. Analytical prediction of magnetic field in permanent magnet motors with Rotor eccentricity based on the method of equivalent remanence[J]. Transactions of ChinaElectrotechnicalSociety，2009，24（5） ：7-12.

宋志環.永磁同步电动机电磁振动噪声源识别技术的研究[D].沈阳：沈阳工业大学，2010.

张冉.表面式永磁电机电磁激振力波及其抑制措施研究[D].济南：山东大学，2011.

张磊.车用永磁同步电机径向电磁振动特性[J].电机与控制，2012，16（5）：34-39.Zhang Lei， Wen Xuhui. Radial electromagnetic vibration model characteristics of PMSMs for electric vehicles[J]. Electric Machines and Control， 2012，16（5）：34-39.

左光曙，刘晓璇，于胡明等.永磁同步电机电磁振动数值预测与分析[J].电工技术学报，2017，32（1）：25-30.

Zuo Guangshu， Liu Xiaoxuan， YuHuming. Numerical prediction and analysis of electromagnetic vibration in permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society， 2017，32（1）：25-30.

Guillaume Verez，Georges Barakat，Yacine Amara，Ghaleb Hoblos.Impact of pole and slot combination on vibrations and noise of electromagnetic origins in permanent magnet synchronous Motors[J]. IEEE  Transactions on Magnetics， 2015，51（3）：101-104.

Ilhan Ayd?n，Mehmet Karak?se，Erhan Ak?n. Combined intelligent methods based on wireless sensor networks for condition monitoring and fault diagnosis [J]. Journal Intelligent Manufacturing，2015， 26（4）：717–729.