信号与系统教学浅探

2019-01-17祝常健张红

教育教学论坛 2019年49期

祝常健张红

摘要：信号与系统是电子信息类专业学生在大学阶段的基础专业理论课。这门课主要学习如何使用科学的方法描述生活中的信息以及信号的分析和处理过程。课程内容是学生从中学阶段的被动式学习过渡到高等教育阶段的主动式学习的关键节点，包含了培养学生进行更高层次的科学理论学习和培养具备科学理论创新能力的基础理论知识。然而，在这门课的教和学的过程中一直存在很多的问题，使得很多大学生没有及时掌握这门课的内容，为后续的知识学习造成了困难。为了使学生能够快速地接受和掌握该门课程内容，文章从信号与系统课程内容特点分析和探讨这门课的一些教学思路。

关键词：信号和系统;时域;频域;傅里叶变换;拉普拉斯变换

中图分类号：G642.41 文献标志码：A 文章编号：1674-9324（2019）49-0219-04

一、引言

信号与系统是一门电子信息类专业的基础理论课程。信号与系统主要是学习如何使用科学的数学方法描述生活中的信息。课程内容是学生从中学阶段的被动式学习过渡到高等教育阶段的主动式学习的关键节点，包含了培养学生进行更高层次的科学理论学习和培养具备科学理论创新能力的基础理论知识。特别是在进行科学研究的时候，信号与系统是最基础的知识和方法。其中的知识可以延伸应用到其他的学科领域，比如机械、控制、化学、材料学和生物等。信号与系统中的许多知识，比如冲激函数和频域分析（傅里叶变换）方法，不仅仅是一个描述生活信息的数学工具，更是一种可以彻底颠覆一个人以前世界观的思维模式。但是，信号与系统的数学公式大部分看起来太复杂了，所以很多初学者乍一看就懵圈并从此对它深恶痛绝。如此重要的课程知识，信号与系统居然成了现在大部分高校学生学习的杀手课程。

为了让学生在学习信号与系统过程中不再是枯燥难学的感觉，让学生快速地掌握这门课程，国内的许多高校教师进行了这门课的教学方法的探索[1]。高燕教师在文献[2]中，讨论以创新人才培养为目的的信号与系统教学方法改革和研究。笔者主要是深度结合MATLAB软件的应用，该软件具有良好的数学矩阵运算功能，能够把信号与系统复杂的数学运算用MALTAB代码简单明白地展示。同时还结合计算机网络辅助教学，提高学生的积极性和学习信号与系统的手段的多样性。文献[3]中，以黄山学院为实践教学，根据信号分析与处理课程群建设要求优化教学内容，构建线上、线下和项目驱动方式的教学模式。蔡凡在文献[4]中，探索了面向应用型人才培养的信号与系统的教学方法。谢自梅研究了基于MATLAB作为教学平台，为学生提供一个轻松愉快、高效的学习氛围[5]。类似的角度在文献[6]中也有研究。方伟伟等人基于“雨课堂”研究信号与系统的教学方法，提高学生学习过程中注重预习和提高教学过程中的师生之间交互效率[7]。刘淑玉等人将信号与系统的教学内容与网络分析、数字信号处理、随机信号等课程内容结合起来，合理地安排该门课程的教学内容。笔者还把多媒体教学和传统教学相结合，探索一种让学生系统地吸收信号与系统的教学方案[8]。高诺等人从实验教学的角度对信号与系统的实验教学的体系和内容安排等三个方面进行探索，目的是为了培养学生的学习兴趣、工程实践素养和创新思维等方面的能力[9]。苗丹结合应用型本科院校的特点，从如何培养学生的应用实践能力角度研究信号与系统的教学[10]。另外，吕军等人在文献[11]中提出直观化教学的概念，以提高教学质量和调动学生学习的积极性。

以上的研究成果主要是从教学内容和实验教学角度探索如何提高信号与系统的教学质量和效率。这些研究成果都从比较严肃的角度出发，始终存在让学生无法轻松愉快地接受和掌握信号与系统的知识，还没有一个完整、高效和严谨的教学方案。为了从让学生更加轻松和充满乐趣地学习信号与系统，本文结合在电子信息工程专业学习的教学和学习体会，尝试从知识的特点和教学内容的展示方式上探讨信号与系统的知识讲授方法。

二、课程内容分析

信号与系统是学习信息的描述和处理的工程数学。学习的内容主要是如何建立信息的数学模型，如何处理、分析和研究信息/信号。需要具备的学科知识是微积分、模拟电路、数字电路等课程。在这门学科的发展过程中，许多数学家和科学家，如让·巴普蒂斯·约瑟夫·傅里叶、拉普拉斯和香农等都做出了重要的贡献。

（一）信号的描述方法

信号与系统主要是学习如何使用科学的数学方法描述世界的信息。描述信息的方法主要有图形曲线和函数表达式。曲线主要是指描述信号变换形状的划线，比如正弦和余弦曲线，如图1所示。函数表达式主要是对信息用数学的方法描述，s（n），f（t）等，比如图1中正弦曲线可以表示为y=sin（2πt）。因此，在学习信号与系统的过程中，必须掌握图形曲线和函数表达式的相互对应转换，给出信号可以用划出曲线，同时能够写出对应的函数表达式。

再者，必须掌握信号的分析，周期信号和非周期信号、连续信号和离散信号等分类。在这些常见的函数的基础上，特别是必须掌握奇异函数的表达式子，即冲击函数和阶跃函数。

（二）系统的概述

在对世界的信息进行描述而得到信号后，需要对信号进行处理。那么，信号处理的过程就是系统。信号的产生、传输和处理需要一定的物理装置，这样的物理装置通常称为系统。一般而言，系统（system）是指若干相互关联的事物组合而成具有特定功能的整体。如手机、电视机、通信网、计算机网等都可以看成系统。它们所传送的语音、音乐、图像、文字等都可以看成信号。信号的概念与系统的概念常常紧密地联系在一起。系统的基本作用是对输入信号进行加工和处理，将其转换为所需要的输出信号，如图2所示。在学习的过程中需要掌握系统的输入和输出之间的关系。

（三）信号的变换域

信号与系统中最重要的一个内容就是信号的变换域。在我们日常生活中，我们看到的世界都是以时间作为衡量标准，事情的变化、树木的生长、人的位置的变化都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法称其为时域分析。在随着时间不停变换的过程中，我们很难分析信号的特性。因此，科学家们找到了一种变换域，即频域。我们发现在频域中，世界是永恒不变而且具备一定的特点，这样便于分析和处理信号。在我们的日常生活中，普遍认为世间万物都在随着时间不停地改变，并且永远不会静止。因此，在学生学习变换域这部分内容的时候，根本无法接受，更别说理解了。而这一部分内容是信号處理以及后续课程数字信号处理的核心内容。如果这部分内容没有学习好，根本无法掌握信号与系统的内容。

对于频域，先说一个最直接的用途，就是广播收音机的频段，在收音机接收信号的时候，不同的电台使用的是不同的频道。这里的频道就是不同频段的信道，这里的信道用来传输不同的信息。那么信号的频域有优点呢？我们可以从一个例子开始比如先在纸上画一个sin（x），我们可以很容易画出近似的正弦信号图，如图1所示。接着，如果要求在纸上用笔画一个

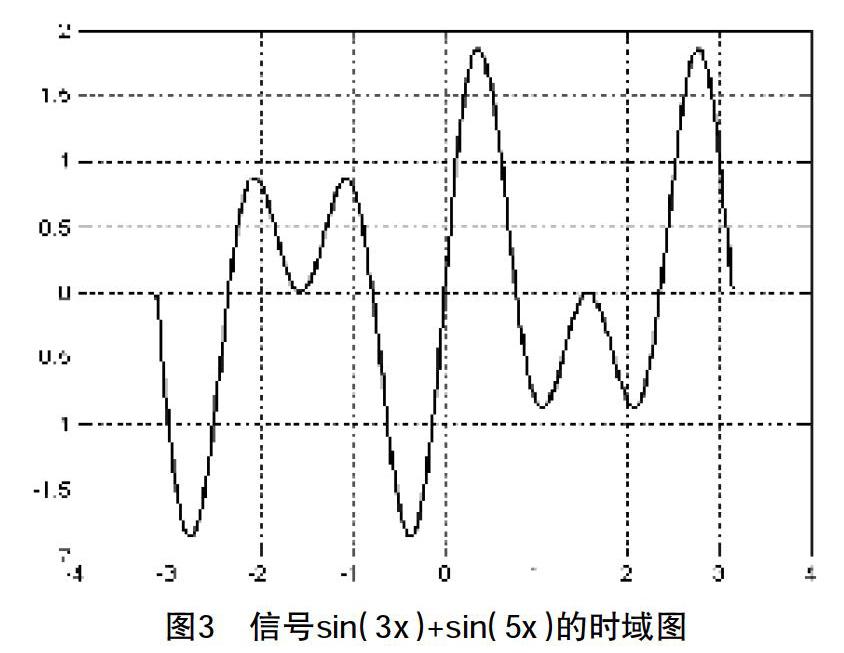
f（x）=sin（3x）+sin（5x）的图形，我们发现根无法完成，因为曲线什么时候上升和下降，我们根本无法画出来。而用MATLAB画出来的f（x）=sin（3x）+sin（5x）的曲线如图3所示。如果再进一步要求，假设我们不知道这个曲线的方程式，现在需要把sin（5x）从图3里拿出去，看看剩下的是什么？我们发现，在时域中这基本是不可能做到。

但是在频域呢？把信号f（x）=sin（3x）+sin（5x）做傅里叶变换后得到的频谱图就是几条竖线而已如图4所示，很容易就可以把不同的信號的谱线找出来，以及可以滤去剩下我们想要的信号。所以很多在时域看似不可能做到的数学操作，在频域很容易，这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分，这在工程上称为滤波，是信号处理最重要的概念之一，只有在频域才能轻松做到。

三、知识点的展示方式分析

通过教学活动我们发现，知识的传授很讲究知识点的展示方式。有时候复杂枯燥的数学公式，可以使用生活中一个简单的例子说明白，或者是使用一个形象的图来展示，提高教学的质量。

（一）结合生活例子解释概念

信号与系统的理论知识其实也是源于生活。在进行教学活动的时候，不能够脱离生活中的应用纯粹讲授数学公式，那样会大大降低教学质量。因此在教学活动中，在一些知识点的讲授过程中，可以适当举一些生活中的例子。例如，我们讲授信号、系统的定义的时候，可以举手机信号发射和接收的例子。如图5所示，手机会采集生活中的信息，包括文字、图片、语音、视频等，然后经过手机的处理就发射出去，在另外的接收端手机就会接收下来处理，再显示。手机拍摄的人、大楼、树、汽车等世界中的各种事物和事情就是信号，两部手机一发送一接收就是一个完整的系统。通过举这样的生活中的手机例子，就可以把信号与系统的定义讲述清楚。

（二）结合图形的知识内容展示

对于一门工程数学，无论是在讲授信号的内容还是系统的内容的过程，我们发现都是一些繁杂的数学公式。那么我们应该想办法，尽可能地把这些数学公式的知识点用一些简单易懂的图形来描述。比如在讲授傅里叶变换的定义的时候，公式的表达就是

以上就是完整的傅里叶变换公式，如果直接讲述这两个公式的字面意思，很多学生根本无法理解傅里叶变换的物理意义，也不知道什么是傅里叶变换。先举个例子：在我们的理解中，一段音乐是什么呢？

我们对音乐最普遍的理解是，音乐是一个随着时间变化的震动。但我们相信，对于乐器手们来说，音乐更直观的理解是一个个的音符图。具体为在时域，我们观察到钢琴的琴弦一会上一会下地摆动，就如同波浪的走势;而在频域，只有那一个永恒的音符，也就是一个基本的余弦信号。傅里叶变换理论告诉我们，任何周期函数都可以看作不同振幅、不同相位正弦波的叠加。这样对于任意的音乐信号，我们可以理解为利用对不同琴键不同力度、不同时间点的敲击，可以组合出任何一首乐曲。

类似地，任何信号都是由一组基本的正弦波组成，随着正弦波数量逐渐地增长，它们最终会叠加成一个信号。随着叠加的递增，所有正弦波中上升的部分逐渐让原本缓慢增加的曲线不断变陡，而所有正弦波中下降的部分又抵消了上升到最高处时继续上升的部分，使其变为水平线。我们能想到的任何波形都是可以用正弦波叠加起来的。这是没有接触过傅里叶分析的人在直觉上的第一个难点，但是一旦接受了这样的设定，后面的学习就开始变得有趣起来了。比如信号的频谱都是通过多个正弦信号的叠加，从频率轴观察得到，如下页图7所示。

在图中，最前面显示的频谱线就是所有正弦波叠加而成的总和。它是由多个正弦信号在后面依不同颜色排列而成的，正弦波就是组合为这个信号的各个分量。这些正弦波按照频率从低到高从前向后排列开来，而每一个波的振幅都不同，从而构造成任意的信号。基于以上的展示，我们可以发现频谱其实就是信号叠加图，从另外一个角度看得到的图形，从频域方向看到的就是频谱。这样比纯粹用数学公式解释的傅里叶变换要直观得多。

四、总结

本文以结合图形方法和生活例子的内容展示方式初步探讨信号与系统的教学方法。目的是避免枯燥的数学公式给初学者造成的学习的困难，以更加快乐和高质量地掌握信号与系统的知识，从而提升学生学习信号与系统及其相关科目的兴趣，克服畏惧心理，做到真正掌握信号与系统相关知识，为进一步深造打下坚实的理论基础。

参考文献：

[1]陈万培，储诚明，胡学龙，等.独立学院电子信息工程专业人才培养模式的实践[J].工业和信息化教育，2013，（1）.

[2]高燕.以创新人才培养为驱动的信号与系统课程改革研究[J].中国教育技术装备，2017，（22）：42.

[3]吕军，宁仁霞，孙剑，等.面向应用型人才培养的信号与系统课程教学改革研究——以黄山学院为例[J].黄山学院学报，2017，（05）：122-125.

[4]蔡凡，朱同波.基于应用型人才培养的“信号与系统”课程改革与探索[J].收藏，2018，（1）：92.

[5]谢自梅，范黎林.基于MATLAB的促进师生共同发展的《信号与系统》课程教学改革[J].教育教学论坛，2018，（11）：103-107.

[6]王侠，顾明亮.MATLAB在《信号与系统》课程中的应用[J].中国科技信息，2007，（12）：248-249.

[7]方伟伟，李鉴，黄照光，等.基于“雨课堂”的《信号与系统》课程教学改革实践[J].现代计算机：上下旬，2017，（17）：25-28.

[8]刘淑玉，赵伟，胡明华.关于电类方向信号与系统课程全面改革的几点措施——知识体系的完善与习题，实验的改进[J].科教文汇，2017，（2）：63-65.

[9]高诺，耿淑娟，杨红娟.“信号与系统”实验教学改革探索与成效[J].教育教学论坛，2017，（19）：152-153.