基于支持向量机的石墨电极电火花深窄槽加工工艺预测研究
2019-01-17迟关心李文通贾雨超刘洪政
迟关心,李文通,贾雨超,刘洪政
(哈尔滨工业大学机电工程学院,黑龙江 哈尔滨 150001)
电火花加工因具有不受材料硬度限制、无宏观切削力、可加工任何导电性材料等特点而被广泛应用[1]。但是,加工效率低、损耗大的问题一直困扰着电火花加工的发展,在某些场合已逐渐被高速铣削所替代。然而,在航空航天、模具行业中多存在一些深窄槽结构,这种特殊结构因深宽比较大及材料硬度的限制,导致传统加工方法无法完成,故电火花仍然是最有效的加工方法[2]。
电火花深窄槽加工除了具有普通成形加工的特点外,还存在其特性。随着加工深度的进行,电蚀产物难以排出,加工条件的恶化导致不良放电现象增多,不仅造成加工效率下降,还带来电极损耗的增大,采用石墨电极加工时这种现象更明显[3]。石墨被蚀除后,产生的大量微小颗粒分布在极间间隙,导致加工环境恶化,易发生拉弧、集中放电、局部积碳等不良现象,严重影响加工效率和工件质量,致使电火花加工参数的调控受到限制,可选参数范围窄,最佳参数组合更难以决策,在这种情况下优化加工参数是必不可少的[4]。
参数优化一直是电火花加工的研究方向之一,学者们在这方面做了大量的工作,提出和引进了多种电火花加工参数优化方法,大致可分为二种[5]:一种是借助于实验设计,通过对实验数据的直接分析得到最佳参数组合,如Vijay Verma[5]设计了四因素二水平的全因素实验,通过方差分析明确Ti6Al4V电火花加工时各因素对加工效率和表面粗糙度影响的大小;Chandramouli[6]和Mishra[7]设计了正交试验,用信噪比分析的方法分别得到铜钨电极电火花加工不锈钢PH17-4和EN-24合金钢时的最佳参数组合;Anand[8]通过灰关联分析得到磁场辅助和普通电火花加工两种情况下的最佳参数组合;Vinoth Kumar[9]用灰关联分析方法对冷却电极和非冷却两种情况作了多目标优化,得到加工效率较高、损耗较小、表面粗糙度较好的参数组合。另一种参数优化方法是建立工艺模,利用模型进行分析、预测,并通过对模型的求解得到最优解或最优解集,如Tamang[10]用线性回归的方法建立电火花微孔加工的直径过切和锥度的回归模型,通过适应度函数的设计将两个目标映射到相同区间转化为单一值实现多目标优化,提高了微孔加工质量;Kumar[11]用非线性回归的方法建立线切割加工Inconel 718时的加工速度和表面粗糙度的回归方程,用NSGA-II算法实现了多目标优化,并通过信噪比和方差分析量化各因素对实验结果的影响大小;Ved Raj Khullar[12]和Milan Kumar Das[13]用响应面分析方法分别建立了不同冲液方式下AISI5160钢和EN31工具钢的电火花加工工艺模型,用不同算法实现单目标和多目标的求解。Aich[14-15]通过支持向量回归机建立了电火花加工工艺模型,并对支持向量机模型相关参数的决策进行了研究,对用粒子群优化算法、教与学算法建立起来的模型进行了比较;张凌瑄[16]通过支持向量回归机分别建立了电火花微孔加工的电极损耗和加工时间的工艺模型,以此模型作为遗传算法的适应度函数,用非支配排序的方法实现了多目标优化。Conde[17]和Jafari[18]通过神经网络建立了电火花加工工艺模型。
组合优化的方法操作简单,但只能得到单一组合;建立工艺模型虽然过程繁琐,但若模型足够精确,则可定性、甚至定量地预测和分析工艺,节省工时。在建模方法中,神经网络被大量使用,但由于神经网络对数据量要求很大,且缺乏明确的理论指导,模型参数的选择只能依靠经验或试错法;线性或非线性回归的方法虽然简单,但模型预测误差较大;建立在统计学习理论之上,以结构风险最小化为原则的新一代机器学习和数据处理方法——支持向量机,克服了传统及其学习“维数灾难”、“过学习”等困难,能根据有限的样本信息在模型复杂性和学习能力之间寻求折衷,特别适合解决小样本、非线性、高维数的问题。本文研究了支持向量机回归分析方法在建立石墨电极电火花深窄槽加工工艺模型中的应用,并证明了该方法的有效性。
1 支持向量机回归基本原理
非线性的支持向量机回归是通过某种非线性变换将数据集转换到高维空间并在其中构造线性最优决策函数,即最优近似超平面。线性回归就是找一条与训练点偏离最小的直线,对于支持向量回归就是寻找最优近似超平面。
对ε-线性近似训练样本集S:
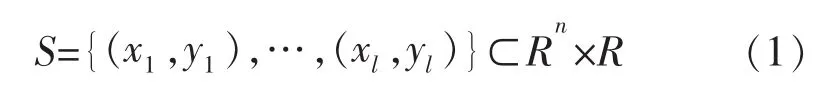
存在超平面f(x)=
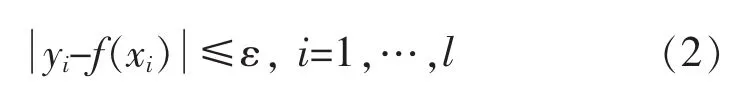
则样本点(xi,yi)∈S到超平面f(x)的距离为:
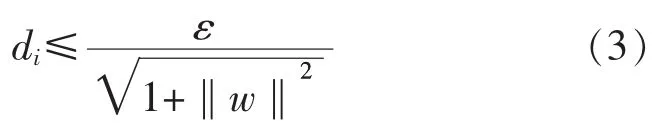
最大化距离的上限得到:

约束条件为:
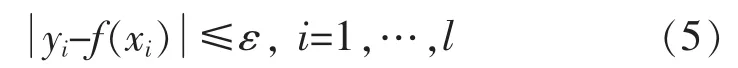
引入松弛变量:
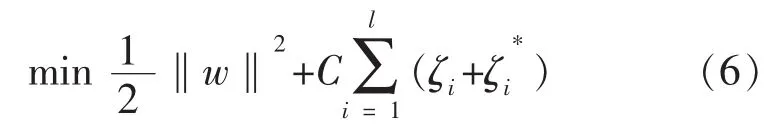
约束条件为:
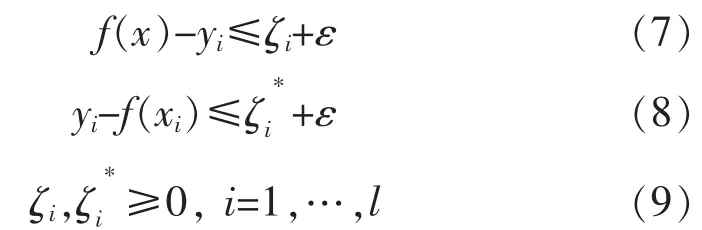
式(6)中的第一项使函数更加平坦,提高了模型泛化能力;第二项为减小误差,常数C称为惩罚因子,对两者做出折衷,起到平衡的作用。ε为一事先给定的正常数。
引入拉格朗日函数得:
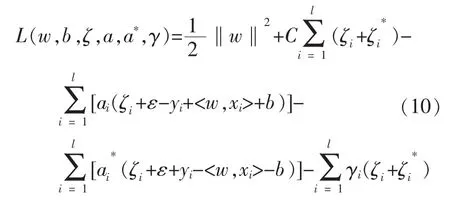
式中:ai、、γi≥0,i=1,…,l为拉格朗日系数。
根据极值条件有:
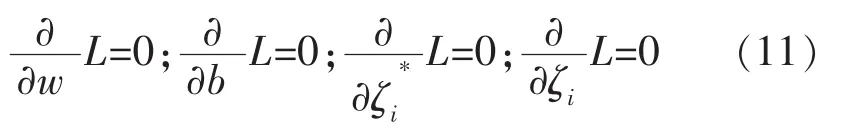
求解式(11)得:
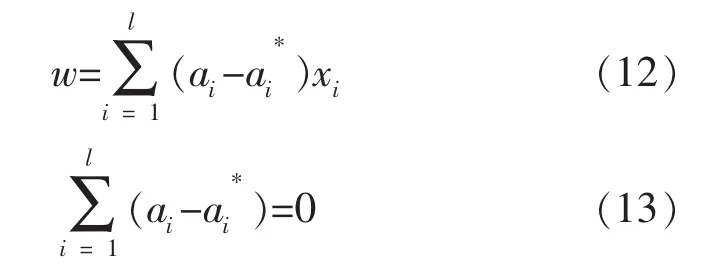
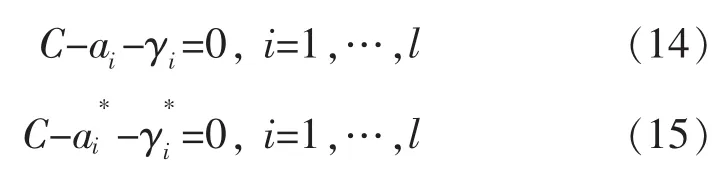
将式(12)~式(17)代入式(10)得到对偶形式:
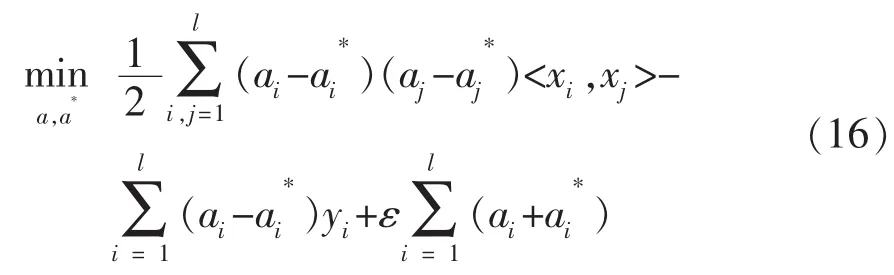
约束条件为:
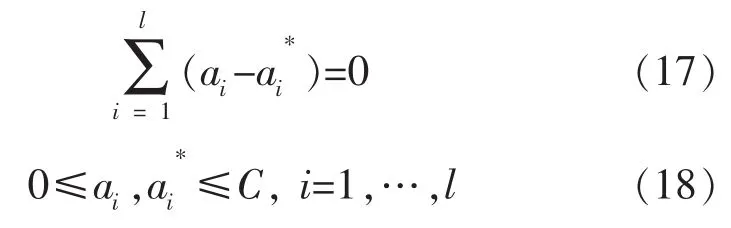
对于非线性回归,首先用一个非线性变换ψ将数据映射到高维特征空间,即用<ψ(xi),ψ(xj)>代替式(16)中的<xi,xj>,并用核函数K(xi,xj)代替高维空间的内积运算<ψ(xi),ψ(xj)>,便达到非线性回归优化方程:
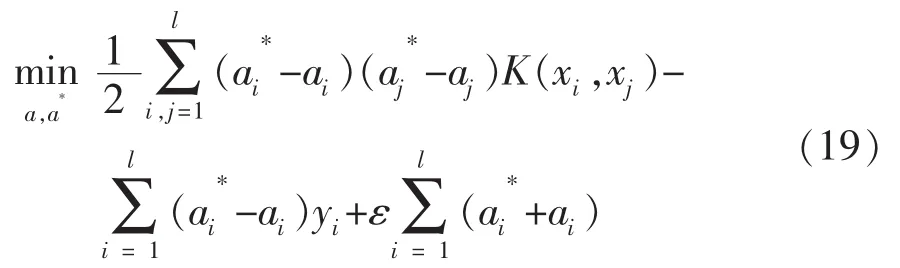
在约束条件式(17)和式(18)下解出a的值,其中不为0的ai或被称为支持向量,于是便得f(x)的表达式:
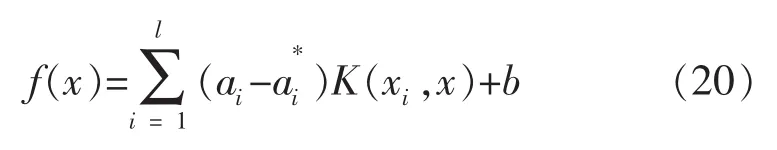
2 石墨电极电火花深窄槽加工工艺实验
2.1 实验准备
实验在DR30B精密电火花成形机床上进行,该机床配备晶体管脉冲电源,能实现三轴联动。同时,电极的装夹、电极与工件的相对位置对实验结果影响很大,因此在实验前均用千分表进行矫正(图1)。实验采用Cr12模具钢作为工件材料,以及选用各向同性石墨ISO-63作为电极材料,其截面积为1 mm×20 mm,加工深度为20 mm。
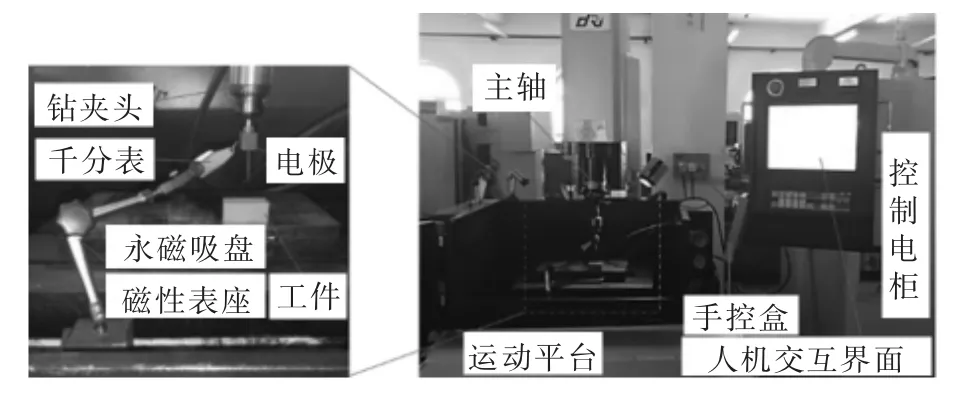
图1 DR30B电火花成形机床及其电极的装夹和矫正
2.2 实验评价
(1)加工效率 MRR
用体积加工速度来表征,即单位时间内工件被蚀除掉的体积:
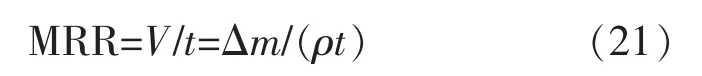
式中:V为工件蚀除体积,mm3;t为加工时间,min;△m为工件蚀除质量,g;ρ为工件材料密度,g/cm3。
(2)电极相对损耗EWR
用体积相对损耗来描述,即电极损耗速度与工件蚀除速度的比值的百分比:
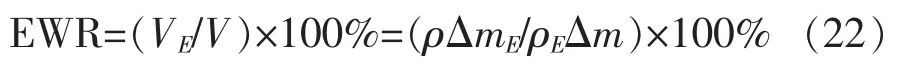
式中:VE为电极的体积损耗,mm3;ρE为电极的密度,g/cm3;△mE为电极的蚀除质量,g。
如图2所示,深窄槽加工时电极存在长度损耗、角损耗和侧面损耗三种形式,电极损耗造成加工槽的不规则,很难直接测得精确的工件蚀除体积和电极损耗体积。为了保证实验结果的精确性和一致性,工件蚀除体积和电极损耗体积均通过测量加工前、后的质量变化,然后分别除以其密度得到。测量工件和电极的质量采用JJ1023BC型电子天秤,其分辨率为1 mg,最大称重为1020 g。

图2 深窄槽加工样件
2.3 实验设计及结果
正交试验设计具有“均匀分散,齐整可比”的特点,利用该设计方法使实验数据点遍布整个参数范围且均衡分布,能有效地从较少实验量数据中分析各工艺参数和实验结果之间的关系,充分挖掘潜在的优参数组合。以脉冲宽度(ON)、峰值电流(IP)、占空比(Ratio)、伺服参考电压(SV)、加工时间(DN)五因素作为考查对象,设计五因素四水平L16(45)正交试验。因素水平设计见表1,实验结果见表2。
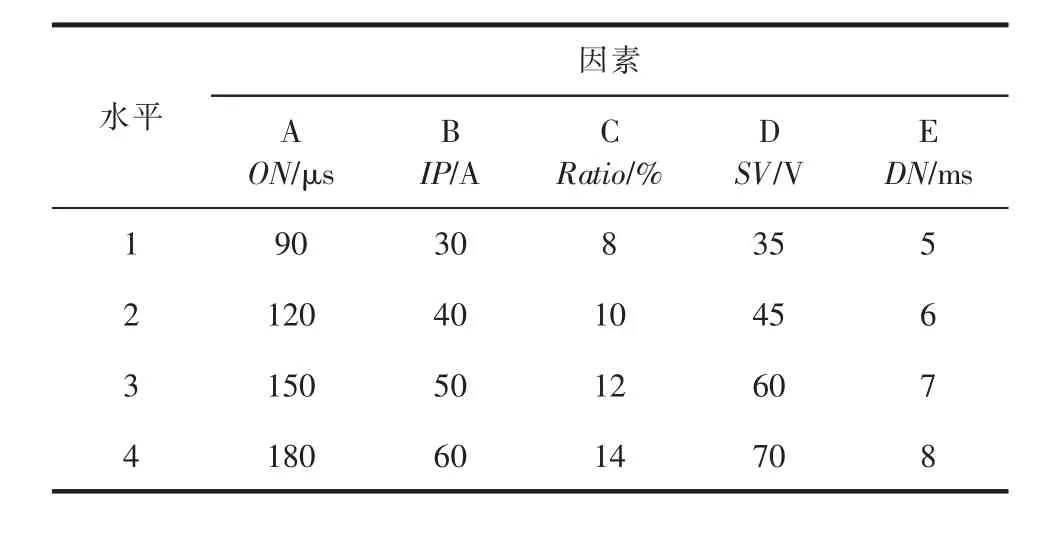
表1 因素水平表
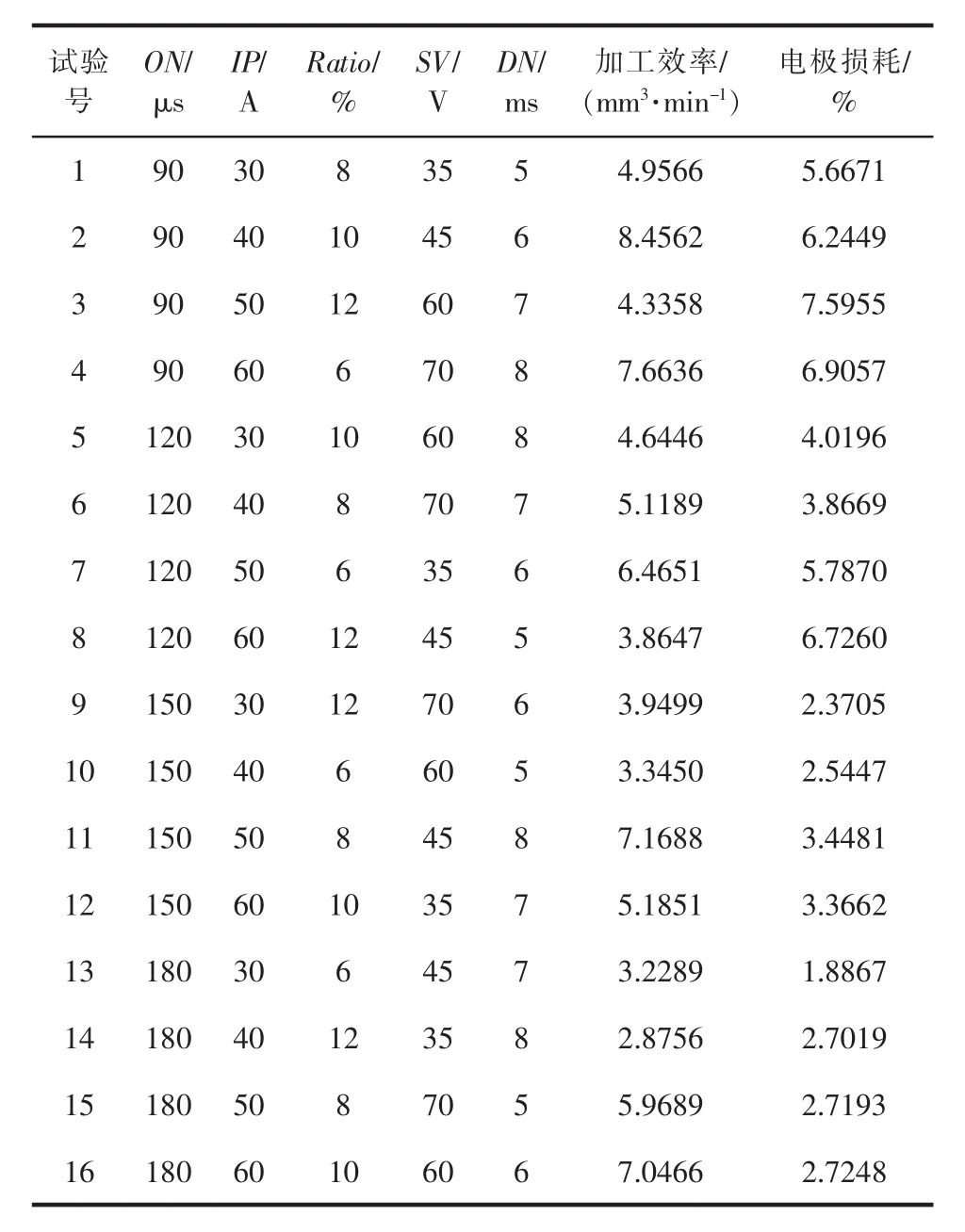
表2 正交试验安排及实验结果
3 支持向量机回归模型的建立
3.1 训练样本预处理
以正交试验数据作为原始数据,但从表2中可看出各因素之间不仅量纲不同,而且数值大小也存在很大差异,故需进行预处理,将数据做0-1之间的归一化处理:

式中:y为归一化处理后的参数值;x为待处理的参数;xmin为参数的最小值;xmax为参数的最大值。
3.2 支持向量机模型参数寻优
在缺乏对所研究样本的先验知识时,采用RBF核函数配合合适的参数选择能取得很好的效果[19],因此选择径向基RBF函数作为模型的核函数:
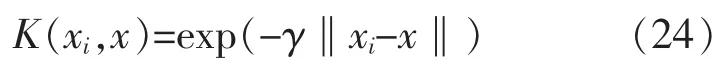
其他相关参数惩罚因子C、核参数γ、不敏感损失函数ε,先设置一个范围和迭代步长,然后用具有全局搜索能力的网格搜索算法进行寻优。
3.3 支持向量机回归模型的训练
在Matlab平台上运用Libsvm工具箱[20],以均方误差MSE作为模型训练效果的评价指标,结合使用网格搜索和留一法进行训练,模型的建立流程见图3。经多次训练后,最终得到模型的相关参数(表3)。
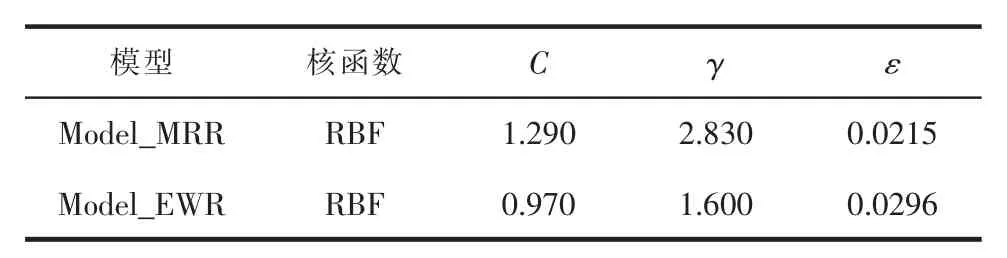
表3 支持向量机回归模型相关参数
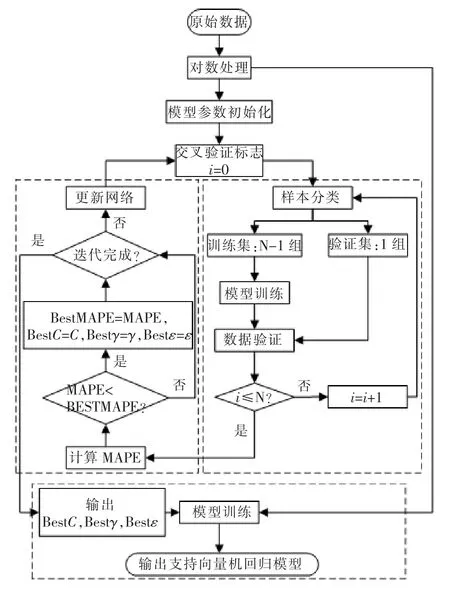
图3 支持向量机回归模型的建立流程
4 模型的实验验证与分析
建立工艺模型后,模型的相关参数是未知的,为了验证模型的预测效果,利用8组未参与训练的数据对模型预测效果进行实验验证。实验值和预测值的结果见表4,模型的预测效果见图4和图5。可看出,模型对材料去除率和电极相对损耗率的预测值和实验值变化趋势一致,预测值在实验值附近波动。据此计算模型的预测误差并绘制如图6所示的柱状图,可见,模型对加工效率的预测误差最大为15.385%、最小为1.38%,平均预测误差为5.82%;对电极相对损耗的预测误差最大为11.53%、最小为0.55%,平均预测误差为4.27%。由于电火花加工本身存在很大的随机性,实验结果复性不好,该误差对于电火花加工来说在可接受的范围内,能定性和定量地分析石墨电极电火花深窄槽加工工艺。
5 结束语
本文设计了五因素四水平的正交试验,以实验结果作为训练样本,利用支持向量机回归的方法分析建立了电极相对损耗和加工效率的工艺模型,并进行了实验验证。结果表明,电极相对损耗的最小预测误差为0.55%、最大为11.53%,平均误差为4.27%;加工效率的最小预测误差为1.38%、最大为15.385%,平均误差为5.82%。该预测误差对于电火花加工而言在可接受的范围内,因此该模型可用于定性、定量地分析石墨电极电火花深窄槽加工工艺,进而指导生产实践。
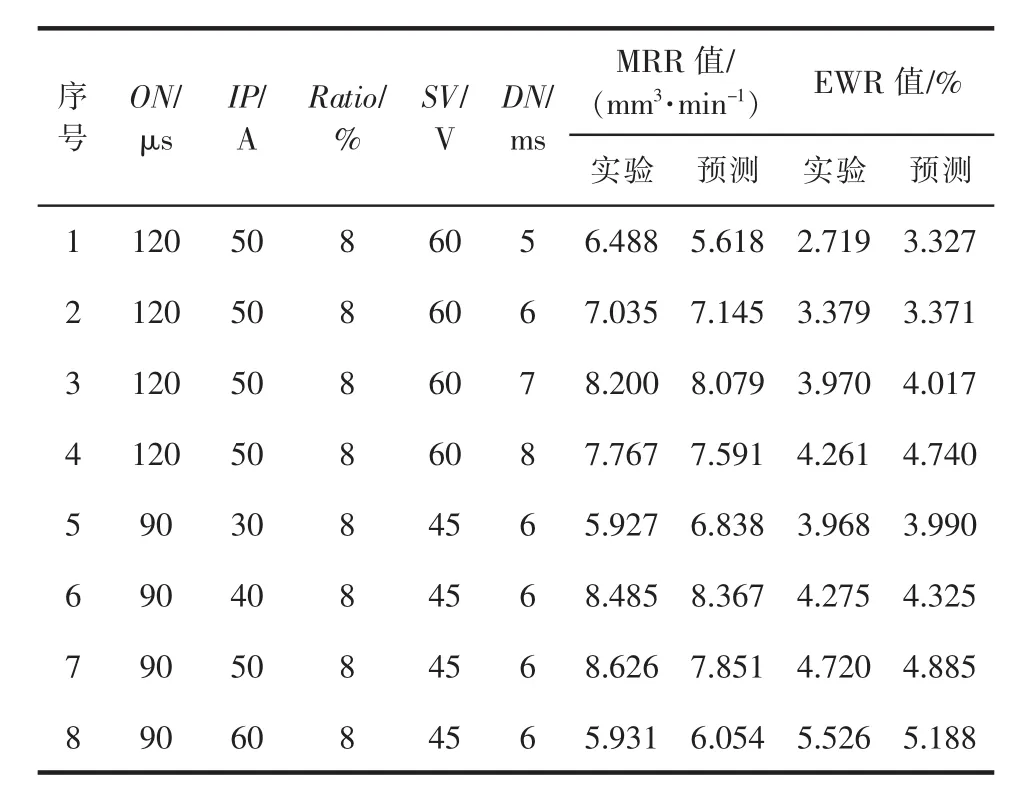
表4 模型实验验证及预测结果
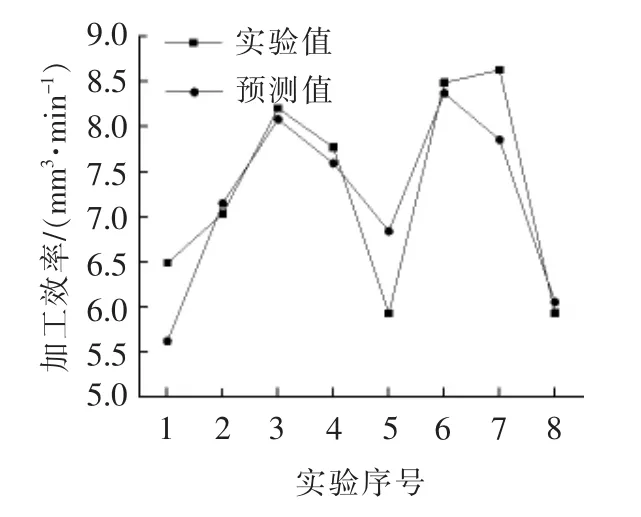
图4 加工效率预测效果
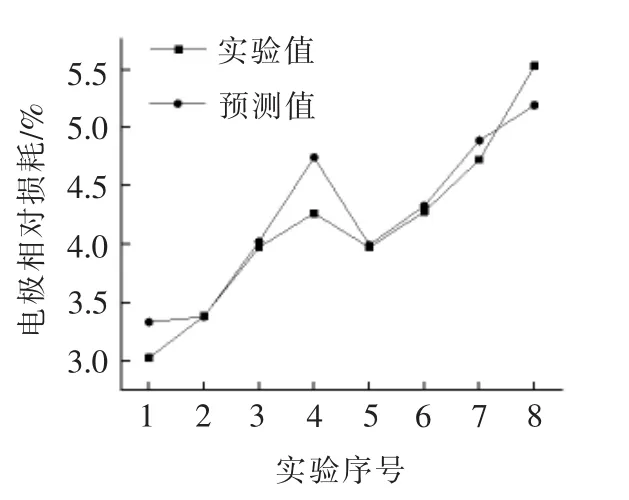
图5 电极相对损耗预测效果
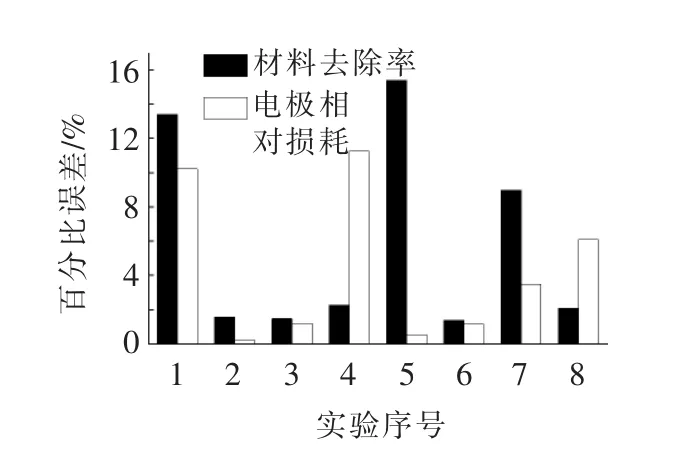
图6 模型预测误差
