基于因子分析与BP神经网络的煤体瓦斯渗透率预测
2019-01-17马晟翔李希建
马晟翔,李希建
(1.贵州大学矿业学院,贵州 贵阳 550025;2.复杂地质矿山开采安全技术工程中心,贵州 贵阳 550025;3.贵州大学 瓦斯灾害防治与煤层气开发研究所,贵州 贵阳 550025)
煤炭是我国经济快速发展的重要保障。煤矿在井下实际生产过程中,对煤层进行大规模采掘时,煤体所受地应力、瓦斯压力等因素发生变化,致使煤体瓦斯渗透率发生改变,增加由于大规模瓦斯涌出而造成瓦斯灾害事故的危险性。煤层瓦斯运移多是以渗流运动为主,因此如何更加高效、精确预测煤体瓦斯渗透率,对我国煤炭行业安全开采以及我国经济发展均具有重大意义。
近几十年来,大批学者相继展开对煤体瓦斯渗透率相关技术研究。林柏泉等研究证明煤体瓦斯渗透率是反映瓦斯流动难易程度的重要指标[1];李祥春等提出了煤体瓦斯渗透率是研究瓦斯在煤层中运移的基本参数[2];张英华等通过实验与数值模拟研究、分析不同应力对煤体瓦斯渗透率影响规律[3];李红涛等通过三轴渗流实验装置研究了不同坚固性系数对煤体瓦斯渗透特性的影响[4];张朝鹏等研究了不同瓦斯压力条件下煤体瓦斯渗透规律[5];谢丽蓉等研究提出影响煤体瓦斯渗透率主要因素为:有效应力、瓦斯压力、温度、抗压强度[6-8];张炎亮等构建了基于ANFIS的煤体瓦斯渗透率预测模型[9];张学超提出了基于人工智能蚁群算法的煤体瓦斯渗透率预测模型[10];王攀等开展了基于影响因素优选的煤层瓦斯渗透率预测模型研究[11]。这些方法经验证都有一定的局限性,因为这些预测方法均涉及较多的预测指标个数,导致预测出来的结果往往存在准确性低、可靠性差等问题。而因子分析法能够简化相互预测指标之间的联系,获得主要影响因子,即公共因子,从而用个数较少的公共因子替代个数较多的原始数据。
基于因子分析法相关原理,本文提出一种将因子分析法和BP神经网络法相结合的煤体瓦斯渗透率预测方法,即将预测指标经因子分析法处理得到的公共因子替代原有预测指标作为BP神经网络结构的输入层参数,减少了BP神经网络输入层参数个数,简化了BP神经网络结构,提升模型预测准确率。通过实例数据检验改进BP神经网络预测模型可行性与准确性。
1 因子分析法与BP神经网络法原理
1.1 因子分析
因子分析法是一种通过个数较少的几个主要因子去替代个数较多的指标或者要素之间的相互关联关系的方法。在因子分析法中,将相关性比较大的几个变量用同一个主要因子表示,以较少的几个主要因子来代表原始数据中的绝大部分信息,从而简化结构,提高运算效率,但又不影响最终结果的准确性。
具体原理和计算过程如下[12]:
根据原始数据里所包含的数据信息,建立总影响因素矩阵X:
X=(Xij)n×p
(1)
式中,n为数据矩阵的组数;p为影响因素的个数。
依据所建立的总影响因素矩阵X,计算总影响因素矩阵X的协方差矩阵,即相关矩阵R:
R=(rij)p×p
(2)
其中,rij为因素i对j的相关性系数。
依据相关矩阵R,计算它的特征值λi,并按相关矩阵R的大小将特征值λi依次记为λ1≥λ2≥…≥λp≥0,同时计算特征根对应的特征向量γ1,γ2,…,γp。
采用以前q个特征值的累积百分比大于或等于80%选取公共因子个数的方法来确定公共因子个数q的值。
计算因子载荷矩阵A:
A=(a1,a2,…,aq)=(aij)p×p
(3)
建立因子得分模型X=AF+ε,即:
Xi=ai1F1+ai2F2+…+aiqFq+εi
(4)
其中i=1,2,…,p,利用因子载荷矩阵A建立总影响因素矩阵X与公共因子矩阵F的关系矩阵。
如何估计B=(bij)p×p是因子分析中的关键问题,本文通过回归法计算B矩阵,由B矩阵和X矩阵可解出公共因子矩阵F,其表达式:
F=BX+ε
(5)
1.2 BP神经网络
目前,在人工神经网络模型和算法中使用最广的就是多层前馈网络及误差反向传播学习算法,即BP神经网络算法。
BP神经网络模型结构是由输入层、隐含层与输出层3部分结构组成。根据相关理论研究表明,拥有一个隐含层的BP神经网络可以以任意精度逼近任意非线性函数[13]。BP神经网络的学习算法是将原始样本数据输入BP神经网络,经过BP神经网络算法运算得出BP神经网络的实际输出,若所得到的实际输出与期望输出之间的相对误差不能满足误差精度要求,则从输出层反向传播该误差,从而调整BP神经网络模型结构中的权值及阈值,然后重新将原始样本数据输入BP神经网络进行运算,从而使BP神经网络的实际输出和期望输出间的相对误差逐步缩小,直到满足目标误差精度要求为止。
2 因子分析法与BP神经网络预测煤体瓦斯渗透率
2.1 瓦斯渗透率影响因素实例数据
根据煤体瓦斯渗透率相关影响因素研究,得到煤体瓦斯渗透率主要影响因素:有效应力、瓦斯压力、温度与抗压强度。各影响因素原始数据见表1[14]。
2.2 瓦斯渗透率影响因素因子分析
通过SPSS软件的因子分析功能对煤体瓦斯渗透率主要影响因素相关原始数据进行预处理。根据表1中的原始数据,建立25×4的矩阵数据库。选择BP神经网络输入层参数为有效应力、瓦斯压力、温度与抗压强度。运用因子分析法对以上输入层参数进行降维处理,将所得到的公共因子替代原有输入层参数作为BP神经网络新的输入层参数。计算过程如下:
根据因子分析法的原理和方法,运用SPSS软件分别计算各成分的方差贡献率及累计贡献率(表2)、各因素相关矩阵表(表3)与成分矩阵(表4)。选取前q个特征值的累积百分数大于等于80%的因子为公共因子,依照表2结果,选取成分1和成分2作为公共因子,分别用F1和F2表示。
根据因子分析法的原理和方法,运用SPSS软件进行运算,得到成分得分系数矩阵表(表5)和公共因子矩阵表(表6)。
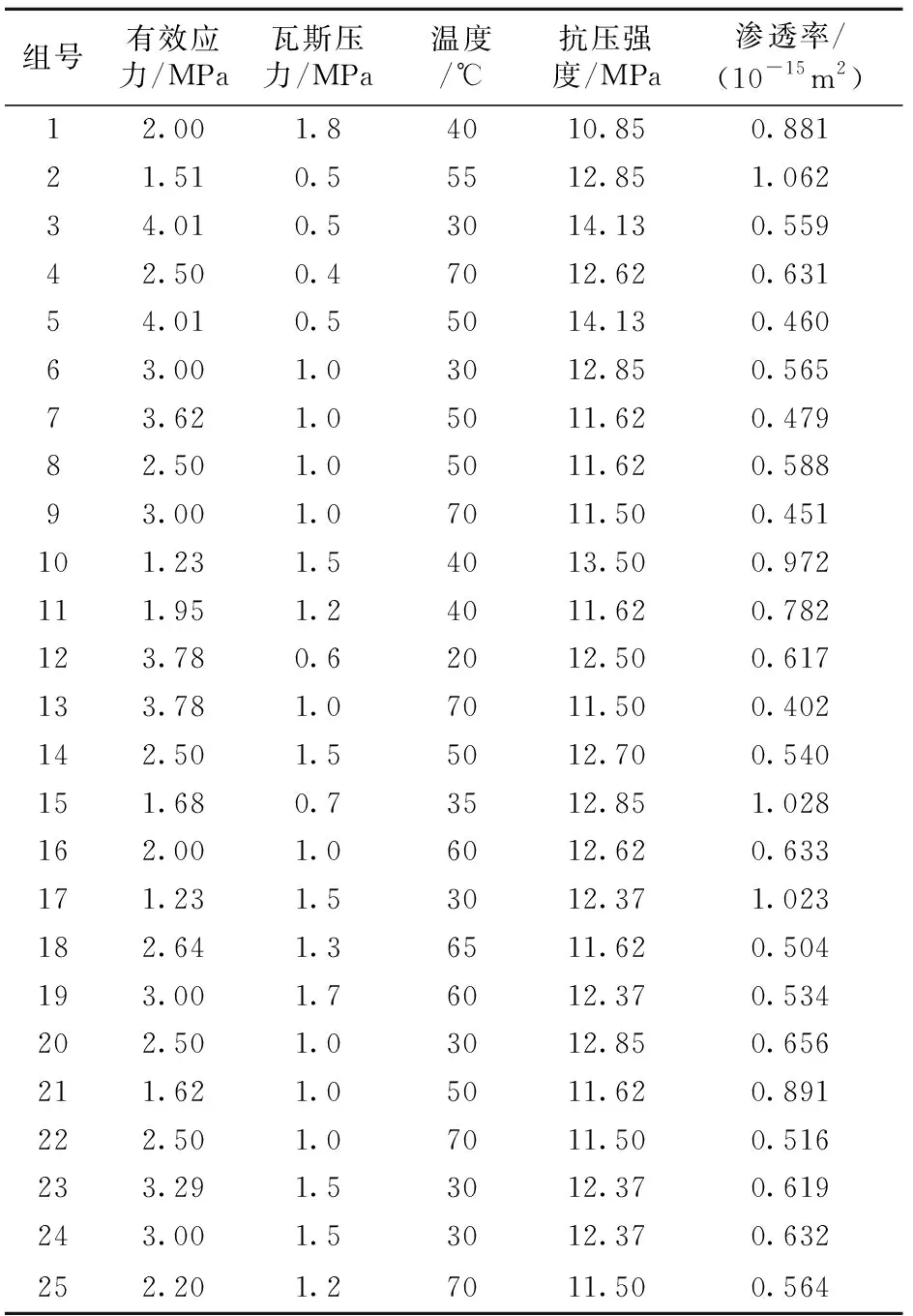
表1 影响因素原始数据
2.3 基于因子分析的BP神经网络瓦斯渗透率预测模型
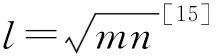
使用Matlab软件中BP神经网络工具箱来创建BP神经网络,将2个公共因子作为输入层参数,煤体瓦斯渗透率作为输出参数,选用tansig函数和logsig函数分别作为隐含层神经元和输入层神经元的转移函数,选用purelin函数和trainlm函数分别作为输出层激活函数和BP神经网络训练函数。设置BP神经网络最大训练次数为250次,BP神经网络训练误差为1×10-7,BP神经网络学习率为0.1,其余BP神经网络训练参数为默认值。将公共因子前20组数据样本作为训练样本,对改进的BP神经网络预测模型进行学习、训练。训练样本预测结果见图1所示,训练样本预测值与实际值之间平均相对误差为0.63%,因此改进的BP神经网络预测模型对训练样本具有很好的拟合效果。

表2 各成分的方差贡献率及累计贡献率
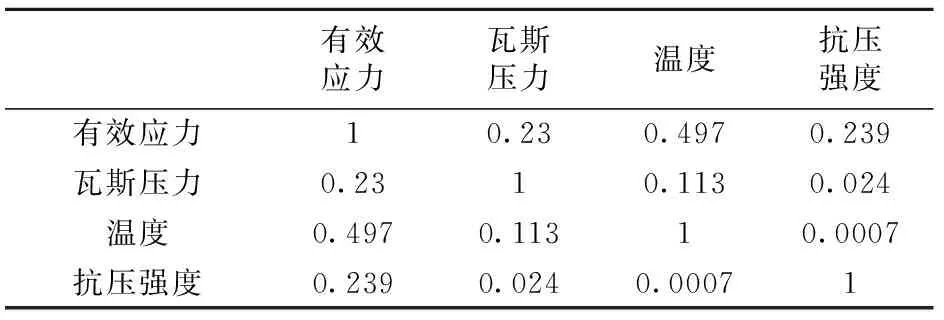
表3 相关矩阵
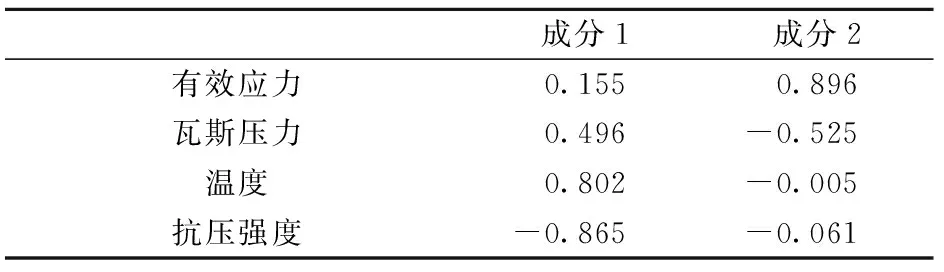
表4 成分矩阵

表5 成分得分系数矩阵

表6 公共因子矩阵

图1 训练样本预测结果
将公共因子最后5组数据样本作为预测样本,为检验改进的BP神经网络预测模型预测性能,分别采用改进的BP模型与未改进的BP模型对煤体瓦斯渗透率预测样本进行预测对比。预测结果如图2、图3所示。
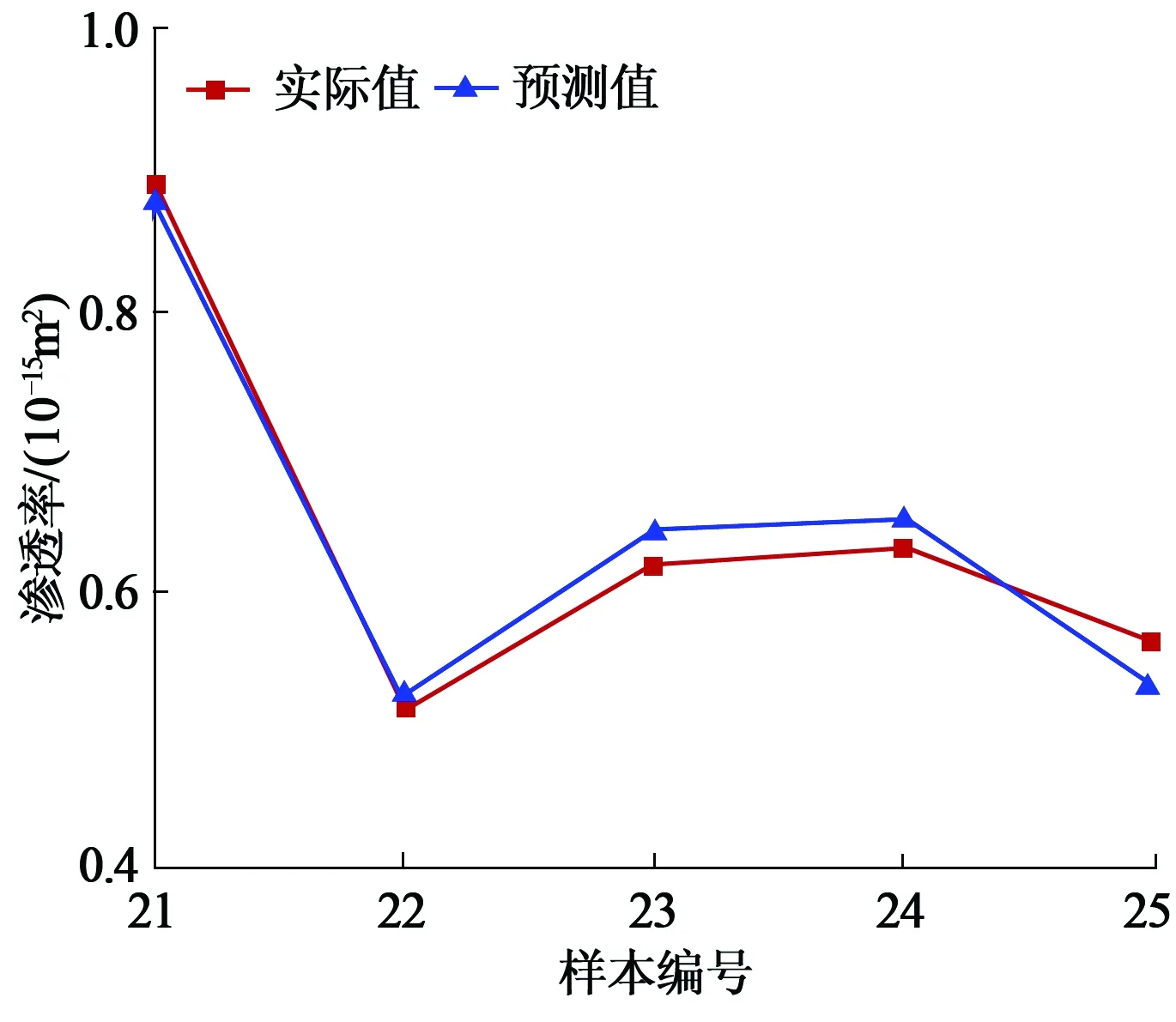
图2 改进BP模型预测样本结果对比

图3 BP模型预测样本结果对比
预测结果是经神经网络预测模型运算得到预测值,期望结果是原始数据中渗透率实际值。如表7、8所示,改进的BP神经网络模型预测样本最大相对误差为5.43%,最小相对误差为1.36%,平均相对误差为3.16%;未改进的BP神经网络模型预测样本最大相对误差为9.44%,最小相对误差为0.63%,平均相对误差为6.37%。对比可得,改进的BP神经网络模型预测相对误差较小,具有良好的煤体瓦斯渗透率预测准确性,适用于煤体瓦斯渗透率预测研究。

表7 改进BP模型预测样本结果

表8 BP模型预测样本结果
3 结 论
(1)本文采用因子分析法对BP神经网络输入层参数进行优化,减少BP神经网络输入层参数个数,以公共因子作为模型输入参数,煤体瓦斯渗透率作为模型输出参数,构建基于因子分析的BP神经网络预测模型。
(2)运用前20组训练样本数据对改进的BP神经网络预测模型进行学习、训练,并将预测值与实际值对比,其相对平均误差为0.63%,证明训练完成的改进BP神经网络模型具有良好的拟合效果。
(3)通过MATLAB软件编程实现了基于因子分析与BP神经网络的煤体瓦斯渗透率预测。并通过改进BP模型与传统BP模型对5组预测样本的预测,其结果为:改进BP模型预测样本平均相对误差为3.16%,传统BP模型预测样本平均相对误差为6.37%,证明改进BP模型预测精确度优于传统BP模型。
