基于粒子群算法的电液控制液压支架自适应调节方法
2019-01-17李海锋
李海锋
(中国煤炭科工集团太原研究院有限公司,山西 太原 030032)
液压支架作为煤矿综采工作面关键机电装备之一,是保证煤矿安全生产的重要支护设备[1-2]。传统的人工操作液压支架升架、降架时,均靠人眼观察降架、升架情况,动作耗时通常比实际需要的要长。装有支架控制器的液压支架[3-5],在执行降架、升架动作时,通常按照控制中已设定的动作来执行相应动作,这种控制方式存在执行动作耗时多于实际所需时间的问题。2015年于贵等[6]对液压支架四连杆机构进行动态仿真,进行了支架机构优化。目前对液压支架按照设定的动作程序进行动作分析的方法及缩短支架动作时间的技术研究较少。为了提高工作面自动化及煤炭开采效率[7-8],对缩短液压支架机构运动时间进行研究具有重要意义。
1 电液控制液压支架控制回路及姿态分析
液压支架的主要动作有降架、移架、升架和推
移刮板输送机[9-10]。电液控制液压支架的动作由乳化泵站提供高压乳化液,通过支架电液控制系统控制不同功能的电磁转向阀,进而使液压缸动作来实现支架机构动作,整个综采工作面的支架共用一个泵站作为动力源[11-12]。本文主要研究减少支架“降架—移架—升架”动作时间的方法,涉及到的液压缸主要有立柱、平衡千斤顶和推移千斤顶,这里称驱动这3组液压缸的电液控制回路为“降架—移架—升架”基本控制回路,如图1所示。

1—平衡千斤顶;2—立柱;3—推移千斤顶;4—刮板输送机; 5,6,7—电磁换向阀;8—泵站;9—支架控制器图1 液压支架“降架-移架-升架”动作基本控制回路
液压支架在降架后、升架前,即移架时的姿态称为支架的过渡姿态。如图2所示,直线代表支架顶梁,曲线代表顶板曲线。

图2 移架过渡姿态
在同一顶板条件下,满足顶梁在移架时不会碰到顶板这个条件的过渡姿态有很多,必然存在一个过渡姿态使得“降架—移架—升架”动作耗时最短。如下式所示:
(1)
(2)
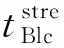
2 粒子群算法及活动空间
2.1 粒子群算法介绍
粒子群算法(POS)也称粒子群优化算法,是一种基于模式的优化算法,它通过追随当前最优值来寻找全局最优[13-15]。如图3所示,在连续空间坐标系中,粒子群算法的数学模型描述如下:

图3 粒子群算法中各矢量之间的关系
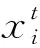
(3)
(4)

2.2 粒子群算法流程
粒子群算法是一种并行算法,其基本步骤如下:
步骤1:初始化参数。在位置空间中随机产生粒子的速度和位置。
步骤2:评价粒子。对每一个粒子评价为适应度函数的最优值。
步骤3:更新最优。比较粒子适用值与其个体的最优值pbest,如果优于pbest则该粒子的pbest位置就是当前位置;比较粒子适用值与群体最优值gbest,如果当前值优于gbest,则设置gbest位置为当前粒子的位置。
步骤4:更新粒子。按照公式(3)和公式(4)更新粒子的位置和速度。
步骤5:终止条件。进入迭代寻优,重复执行步骤2~4,直到满足终止条件终止执行,即满足适用值和最大迭代代数。
粒子群算法的基本流程图如图4所示。

图4 算法流程
3 支架过渡姿态求解
3.1 适应度函数
本文过渡姿态优化求解,就是在液压支架动作过程中,“降架—移架—升架”的总时间最短,假定支架移架的时间不变,则目标函数简化为降架和升架的总时间为最短,故目标函数式为:
minT=T1+T2
(5)
式中,T1为降架时间,T2为升架时间,具体求解如式(1)和式(2)。
求解方法设计是本论文最重要的一部分,解决最优过渡姿态问题,即在液压支架工作活动区域内求得某一特定姿态,使支架的“降架—移架—升架”动作时间最短。通过支架运动学分析,建立一个二维解空间,粒子群算法中每个粒子都是一个潜在的解,在二维解区间内,每一个粒子的位置问题、速度向量、历史最优位置向量以及全局最优位置向量均用δ,φ表示,则每个粒子的适应度值为它们所处位置的T′(δ′,φ′)值。
3.2 实现步骤
步骤1:设置粒子种群的种群规模为n=20,随机设置粒子的位置和速度。
步骤2:求第i个粒子的适应度T′(δ′,φ′)。
步骤3:对于第i个粒子,若适应度T′(δ′,φ′)优于该粒子的最优值pbest,则令pbest=T′(δ′,φ′)。
步骤4: 对于所有粒子,若某个粒子的适应度优于全局最优gbest,则令gbest=T′(δ′,φ′)。
步骤5:根据公式(3)和公式(4)更新每个粒子的位置和速度。
步骤6:进入迭代寻优,重复步骤2~5,若达到最大迭代步骤或全局最优解差距小于设定值,终止执行。

4 仿真分析及验证
以ZY17300/32/70液压支架为例,该支架采用双伸缩立柱。在“降架—移架—升架”过程中,立柱中缸动作优先于活柱。支架外缸内径400mm,中缸外径380mm,平衡千斤顶缸径230mm,杆径160mm。立柱下腔进液流量为350L/min,中柱活塞腔进液流量、平衡千斤顶下腔进液流量和平衡千斤顶上腔进液流量均为125L/min。代入速度计算公式(3),可以得到降柱速度为0.05m/s,升柱速度为0.023m/s,平衡千斤顶伸出速度为0.05m/s,平衡千斤顶缩回速度为0.097m/s。
液压支架在实际工作中,受顶板下沉等多种因素影响,采煤工作面每推进一刀的支架姿态并不相同。根据液压支架实际的工作状态取10组数据,立柱长度lLeg和平衡缸的长度lBlc如表1所示。
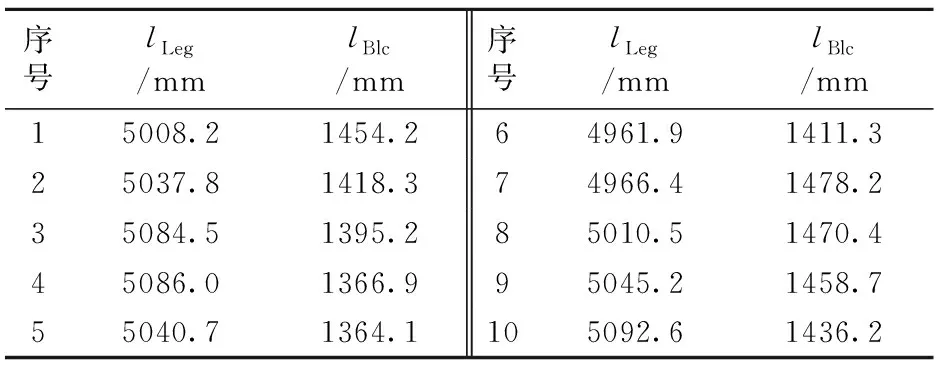
表1 10组截割状态的立柱长度和平衡千斤顶长度
运用本文所述的粒子群算法,以表1为输入条件,进行10次求解,结果如表2至表6所示,表2为支架处于过渡姿态时期望的平衡千斤顶和立柱长度,表3至表6按照降架、升架过程中立柱和平衡千斤顶的动作顺序排列,表3为立柱降柱,表4为降架时平衡千斤顶动作情况,表5为升架时平衡千斤顶动作情况,表6为立柱升柱。
同等型号的液压支架和工况,根据传统的控制方法,支架执行“降架—移架—升架”动作时不调整平衡千斤顶,仅降立柱,首先脱离顶板60mm,移架并升架。液压支架动作的两种方法耗时如表7所示。

表2 10次移架时过渡姿态

表3 10次立柱降柱长度变化和消耗时间

表4 10次降架平衡千斤顶长度变化和消耗时间

表5 10次升架平衡千斤顶长度变化和消耗时间

表6 10次立柱升柱长度变化和消耗时间

表7 不同方法支架动作耗时对比 s
表7中Ttr代表传统方法液压缸动作时间。
从表7中可以看出耗时范围在7~12s内,平均耗时为8.23s。T为本论文采用的方法降架和升架总时间,平均耗时6.91s。Tsh为与传统方法相比“降架—移架—升架”动作缩短的时间。
5 结 论
设计了一种基于粒子群算法的电液控制液压支架过渡姿态最优求解算法,以降架和升架动作总时
间为目标函数,求解具有最短“降架—移架—升架”时间的最优过渡姿态,进而求得立柱和平衡千斤顶的动作顺序和伸缩量,通过该方法得到的“降架—移架—升架”动作时间相对于传统方法,总时间由平均8.23s左右缩短为平均6.91s左右,提升效率超过了20%。
