基于VMD样本熵和AFSA优化ELM的配电网单相接地故障选线方法
2019-01-17田录林王伟博张盛炜陈倩雯
田录林,王伟博,田 琦,罗 燚,张盛炜,陈倩雯
(1.西安理工大学 水利水电学院,陕西 西安 710048;2.工商银行西安高新支行,陕西 西安 710075)
0 引 言
我国6~35 kV配电网广泛采用小电流接地方式,其故障类型主要以单相接地为主,当线路发生单相接地故障时,如何快速找出故障线路具有重要意义。目前配电网故障线路选线方法概括起来可分为如下三种:基于稳态信号的选线方法,基于暂态信号的选线方法,基于人工神经网络的选线方法。①基于稳态信号的选线方法。例如零序导纳法[1]、五次谐波法[2]、零序电流比幅值法[3],这些方法虽然可以对线路进行故障的识别,但其采集的是难以提取有效信息的小数值稳态故障电流信号,从而会影响选线结果。②基于暂态信号的选线方法。线路故障发生时,在所采集的故障波形中其暂态信号所包含的故障信息量远比其稳态信号所包含的故障信息量丰富,因而基于暂态信号的选线方法目前属于主流,主要有小波分析法、暂态能量法、数学形态学、经验模态分解(Empirical modal decomposition,EMD)等。例如文献[4]提出用暂态能量法进行故障选线,但由于消弧线圈产生的感性电流会对零序电流进行补偿,因而可能会对选线结果产生影响。文献[5]利用首半波法选线,该方法虽然不受消弧线圈的影响,但是受短路相位角和电网参数影响较大,易发生误判。文献[6]利用小波分析法和信息熵进行故障选线,虽然小波分析法具有良好的时频特性,但由于小波基函数选择不唯一,其自适应特性较差,对选线结果有影响。文献[7]采用自适应特性较好的EMD分解法分析故障电流信号,但在分解过程中可能会出现虚假分量而导致模态混叠。文献[8-9]通过不同方法提取故障信号特征向量来进行故障选线,但其阈值是根据先前经验设定的,从而对选线结果产生影响。③基于人工神经网络的选线方法,主要包括BP神经网络[10]、支持向量机[11]、学习向量化量(Learning vector quantization,LVQ)神经网络[12]等,以上神经网络算法虽然解决了阈值的经验选取问题,但是参数较多,结构复杂,从而影响选线的速度与精度。
针对以上故障线路选线存在的问题,本文提出基于VMD[13]样本熵[14]和AFSA-ELM的故障选线方法。VMD不但继承了EMD的优势而且避免了信号分解时发生模态混叠。样本熵作为一种度量信号复杂度的工具,可以对故障特征向量进行定量描述。ELM[15]主要解决传统神经网络算法耗时长,训练效率低等问题,它具有参数少,运行速度快、泛化能力强等特点,因而将其应用到故障选线中来具有独特优势。本文还针对ELM中的初始权值和隐含层阈值随机给定的问题,采用AFSA对其参数进行优化,Matlab仿真验证了该方法的有效性。
1 VMD
VMD作为一种自适应、可预设尺度的非平稳信号处理方法,可用于线路故障时的暂态电流、电压信号分析,其核心思想是通过搜索变分模型的最优解,自适应的将信号分解成预设尺度数为K个不同频段的本征模态函数(Intrinsic Mode Function,IMF)分量。该算法主要包括:变分问题的构造和求解。
1.1 变分问题的构造
假设将输入的线路单相接地故障暂态电流信号f(t)分解为K个IMF分量uk(t)(每个模态分量都具有中心频率和有限带宽),且满足K个IMF分量的宽带之和最小和K个IMF分量 之和等于f(t),则带有约束条件的变分模型如式(1)所示:
(1)
式中,{uk}={u1,u2,…uK} 为分解出来的各IMF分量,{ωk}={ω1,ω2,…ωK}为各个IMF分量的中心频率,δ(t)为单位脉冲函数,∂t是该函数在时间t上的偏导数,j表示虚数单位,*是卷积符号。
1.2 变分问题的求解
变分模型式(1)最优解的求解步骤如下:
①引入拉格朗日二次惩罚因子α和拉格朗日乘法算子λ,将式(1)转化为扩展拉格朗日函数式(2)的无约束条件变分模型:
(2)
(3)

③将式(3)经傅里叶变换得到其在频域的表达式(4):
(4)
(5)
(6)
式中,τ为噪声容限参数。
1.3 VMD的算法流程
(2)根据公式(4)~(6)分别更新uk、ωk、λ;
(3)判断是否满足式(7)中收敛条件,满足则停止迭代,否则给n加1继续返回到步骤(2)
(7)
经VMD分解,可将线路单相接地故障暂态电流信号f(t)所包含的故障信息有效地分离出来,最终得到K个IMF分量,为求IMF各分量样本熵做好铺垫。
2 样本熵
作为一种度量非线性序列稳定度和复杂度的工具,参数-样本熵在处理非线性非平稳信号方面得到了广泛应用。例如,系统故障时的暂态电压电流信号越复杂、越不平稳,其样本熵值就越大。样本熵值计算过程如下:
(1)首先用SampEn(N,m,r)来定义样本熵,其中N示输入信号数据的长度,m表示所嵌入的维数,r表示数据的标准差。
(2)假定给出N个点原始时间序列{x(i),i=1,2,…,N},将序列{x(i)}表示为m维向量:
X(i)=[x(i),x(i+1),…,x(i+m-1)]
(8)
其中,i∈[1,N-m+1]
(3)计算向量X(i)与X(j)之间的距离d[X(i),X(j)]则有:
d[X(i),X(j)]=max|x(i+k)-x(j+k)|
(9)
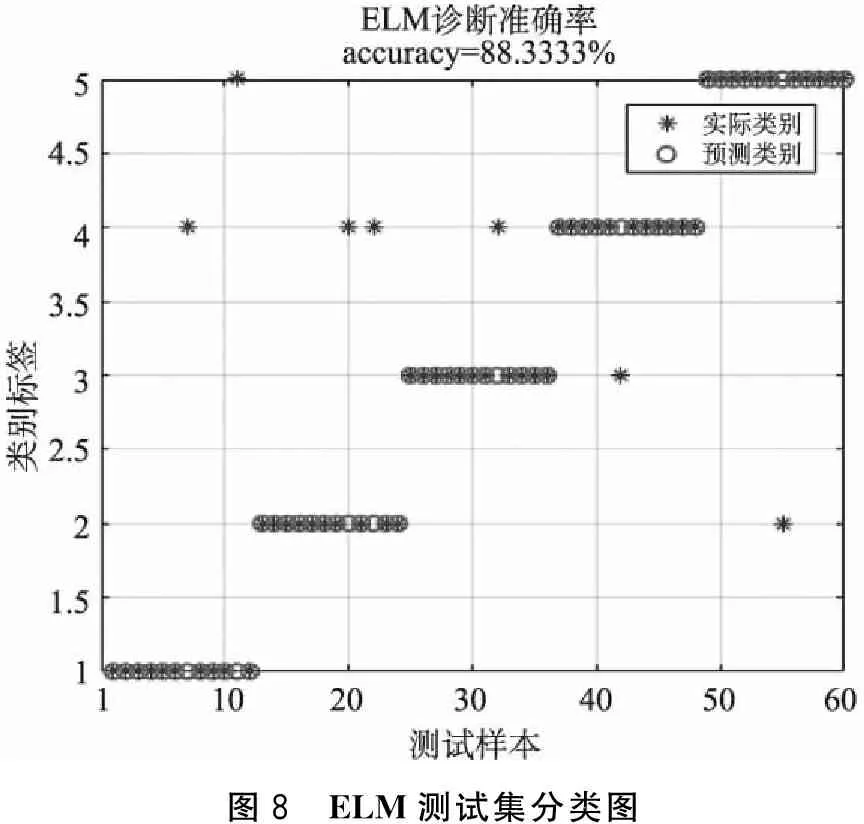
其中,j∈[1,N-m+1],d[X(i),X(j)] (10) 其中,i、j∈[1,N-m+1]且i≠j,r为设定的一个相似容限值且r>0。 (11) (6)对维数m增加一维到m+1,则可得Bm+1(r): (12) (7)则原始输入序列的样本熵为: SampEn(N,m,r)=-ln[Bm+1(r)/Bm(r)] (13) 样本熵可将单相接地故障暂态电流信号经VMD分解得到的K个IMF分量量化放大,从而形成故障特征向量,这对故障分类有利。 ELM算法的主要特点是输入权值和隐含层阈值随机给定,因而只需给定隐含层的神经元个数即可确定最优解。由于ELM是对前向单隐层神经网络的一种改进,因而其模型仍采用前向单隐层模型,如图1所示。 图1 ELM模型 在图1中,设定有n个输入层神经元,m个输出层神经元,l个隐含层神经元。其中ω、β分别表示输入层到隐含层、隐含层到输出层之间的连接权值,具体的矩阵表达式分别如式(14)、(15)所示 : (14) (15) 用b表示隐含层阈值则: (16) 假设原始样本个数为Q,则其相应的输入与输出矩阵分别是X和Y,则相应的矩阵表达式如式(17)、(18)所示: (17) (18) 根据图1可算出其输出Y为: Y=[y1,y2,…,yQ]m×Q (j=1,2,…Q) (19) 在上式中:g(x)为隐含层的激活函数,ωi=[ωi1,ωi2,…,ωin],xj=[x1j,x2j,…,xnj]T。 则式(18)可以表示成为: Hβ=Y′ (20) 其中,Y的转置为Y′;输出的隐含层矩阵为H则: (21) 由Huang等人提出的定理可知:当所给定的激活函数无限可微时,对于任意的ω和b总会有H可逆且‖Hβ-Y′‖=0,也就可以使得网络的训练误差无限接近某个精度值,据此可以计算出β=H+Y′其中H+为H的广义逆矩阵。从而将复杂的网络迭代过程转化为求解逆矩阵的问题,大大简化了计算工作量,提高了网络的运行速度。 由于ELM在训练时的参数ω和b是通过随机选择确定的,所以会导致一些隐含层节点处于无效状态,从而使得ELM的运行速度和精度降低。为了提高ELM的运行精度和速度,本文选择AFSA[16]对ELM的输入权值和隐含层阈值进行优化。AFSA是一种对觅食、群聚、追尾、随机四类鱼类生存行为进行模拟的智能化算法,其特点是通过对鱼群的上述四种行为进行模拟来寻找鱼类个体范围内的局部极值,从而可以在全局范围内寻找到最优值。具体的AFSA-ELM模型的实现步骤如图2所示。 图2 AFSA-ELM模型 用VMD法将采集到的线路接地故障暂态电流信号分解为K个不同尺度的IMF分量,然后求各IMF分量样本熵,再将样本熵所形成的故障特征向量输入到AFSA优化后的ELM中进行训练和测试,得出选线结果,从而实现对故障线路的诊断。具体的故障选线流程如图3所示。 图3 单相接地线路故障选线流程 注:图中的Mi表示第i条线路的样本熵值,i表示系统的总出线数。 本文在Matlab/Simulink中搭建母线为10 kV的配电网模型如图4所示。该配电网中性点为经消弧线圈接地,消弧线圈补偿度为5%,仿真波形的采样频率设置为10 kHz,采样时间设置为0.02 s,5条出线均为架空线路,线路参数如表1、2所示。 表1 架空线路参数表 表2 架空线路长度 图4 配电网模型 设置线路L1在距离母线1 km处发生A相的单相接地故障,设置初相位角φ=90°,接地电阻Rg=10 Ω,则提取故障特征向量的步骤如下: (1)提取当线路L1发生单相接地故障时线路L1~L5的暂态电流信号,由于线路发生单相接地故障的过渡过程十分短暂,因此本文选择线路接地故障后一个周期即0.02 s内的电流信号进行分析。其中采集到线路L1的暂态电流如图5所示。 (2)根据本文1.3节算法流程,将采集到的暂态故障电流信号经VMD分解得到K个IMF分量。本文根据文献[17]的参数选取原则,选择参数K=3,α=2000,经VMD分解得到3个IMF分量如图6所示。 图5 L1线路单相接地故障暂态电流 图6 L1线路单相接地故障暂态电流VMD分解图 (3)将各条线路的3个IMF分量分别进行信号重构,依式(9)~(13)计算各IMF分量的样本熵,再将各条线路所对应的IMF分量样本熵叠加求和得到各条线路的样本熵Mi,构造的样本特征向量T=[M1,M2,M3,M4,M5]。表3给出L1线路在不同故障工况下的各条线路样本熵值。 (1)样本集 选择不同故障线路(L1、L2、L3、L4、L5)、故障位置(20%、40%、80%)、初始相位角(0°、45°、60°、90°)和接地电阻阻值(10 Ω、500 Ω、1 000 Ω),通过Matlab仿真得到180组不同的单相接地故障暂态电流信号,然后经VMD分解并计算各线路的样本熵,形成180个形如T=[M1,M2,M3,M4,M5]的故障特征向量样本,并将样本T进行归一化处理。 (2)AFSA优化ELM的参数,形成最佳参数组合 设置鱼群的种群数为100,最大迭代次数为50,运用AFSA算法对ELM网络的输入层权值矩阵和隐含层阈值矩阵进行参量优化,形成最佳参数组合,有助于提高ELM的运算速度和精度。 (3)线路的故障诊断 将归一化的T=[M1,M2,M3,M4,M5]作为AFSA优化后的ELM的输入,120个样本用作训练样本集,60个样本用作测试样本集;输出为(1、2、3、4、5)五维数据格式,其中1表示线路L1故障,2表示线路L2故障、依次类推5表示线路5故障,测试结果如图7所示。 表3 L1线路部分工况的样本熵 图7 AFSA-ELM测试集分类图 为了与AFSA优化后的ELM进行对比,将上述训练样本集和测试样本集输入到普通的ELM中进行训练和测试,测试结果如图8所示。 图8 ELM测试集分类图 两种方法的对比结果如表4所示。由图表可知:传统的ELM网络测试集中有7组发生了误判,而经AFSA优化的ELM仅有1组发生误判,并且优化后的ELM的仿真时间相比于ELM更短,有效地提高了ELM的选线速度与准确率。 表4 算法分类对比 本文提出基于VMD样本熵和AFSA-ELM的单相接地故障选线方法,主要结论如下: (1)利用VMD方法对不同工况下的线路接地暂态故障电流信号进行自适应分解,避免了模态混叠; (2)样本熵值作为AFSA-ELM模型输入的故障特征向量可定量描述故障信号,有利于故障分类识别; (3)AFSA算法对ELM的输入权值和隐含层阈值优化,可以提高故障识别精度与速度。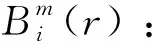

3 AFSA优化的ELM网路模型
3.1 ELM原理

3.2 AFSA优化ELM参数

4 本文单相接地线路故障选线流程

5 仿真验证分析
5.1 仿真模型搭建



5.2 故障特征提取


5.3 AFSA-ELM模型的建立与线路单相接地诊断



6 结 论
