基于运行风险度与马尔科夫链的大坝运行寿命评估

2019-01-16范振东

大坝与安全 2018年6期

范振东

（国家能源局大坝安全监察中心，浙江杭州，311122）

1 概述

大坝运行寿命评估是一个多学科交叉的复杂技术问题，同时受大坝庞大的结构体系、复杂的地质条件和运行环境、材料老化等因素影响，很难对大坝运行寿命进行量化评估[1-2]。然而，对大坝运行寿命进行评估和预测可以为制定大坝除险加固决策提供参考依据，从而在全寿命周期内基于保障大坝安全运行的前提下控制除险加固成本。为此，国内许多专家学者对如何评估大坝运行寿命做了深入研究。如苏怀智[3-4]等提出了基于时变可靠度的大坝使用寿命评估方法，但该方法需要事先假定坝体材料参数时变特性，具有较强的人为主观性。朱伯芳[5]从混凝土碳化、冻融破坏等方面考虑大坝使用寿命，然而由于大坝体积庞大、碳化速率极为缓慢，由此计算出来的使用寿命很长，与实际不符。宋恩来[6]从大坝原型监测数据出发，反演坝体混凝土综合弹性模量的时变规律，但该方法没有建立综合弹模和运行寿命的对应关系，且计算工作量大。

众所周知，大坝的运行性态可以通过原型监测资料反映，因此，大坝的原型监测资料也隐含了大坝运行寿命的客观信息。笔者从大坝监测系统实测资料出发，基于大坝运行风险度，运用马尔科夫链方法对大坝运行寿命评估进行初步探索，为预测大坝运行寿命探索一种新思路。

2 大坝运行风险度评估体系和评判准则

2.1 风险度定义

大坝的运行风险率RI也可称为大坝失事的总概率Pf，其定义可用下列数学表达式表示：

式中：S为相互独立随机变量组成的大坝广义抗力；F为相互独立随机变量组成的大坝广义荷载；fSF(S,F)为荷载F和抗力S的联合概率密度函数。

但多数情况下，受资料缺乏、求解难度大等限制，尚无法根据式（1）直接求解大坝运行风险率RI，因此吴中如[7]提出了根据各种风险因素实测资料来确定大坝运行风险率的方法，并引入了“风险度”的概念来代替风险率，用于表征测点实测成果反映的相应点位处物理量潜在的风险程度，考虑已用的符号，仍用符号RI来表示风险度。

2.2 大坝运行风险度评估体系

大坝运行风险度评估[7]的总目标为估计大坝运行风险度（A层），按风险部位划分，可将准则层（B层）分为坝体风险度、坝基风险度和近坝区风险度，各准则层对应的指标则为影响各准则层风险度的风险因素（C层），监测项目的实测资料可以反映这些风险因素的特性和变化规律，例如，变形测值反映坝体、坝基和近坝区边坡的稳定，相同荷载条件下，应力应变测值变化反映坝体材料力学特性的变化等。大坝运行风险度评估体系如图1所示。

图1 大坝运行风险度评估体系Fig.1 Dam operation risk assessment system

如图1所示，影响大坝安全度的风险因素众多，而这些因素有些是主要因素，有些是次要因素，如果对风险的严重程度进行初步判断，将次要因素从风险因素集中剔除，能大大减少大坝运行风险度分析计算工作。

2.3 大坝运行风险度评判准则

水利部2003年颁布的《水库大坝安全鉴定办法》将大坝分为一类坝、二类坝和三类坝，其中一类坝安全可靠，大坝工作状态正常，在设计工况下能正常运行；二类坝类似于病坝，需要在一定控制条件下运行；三类坝类似于险坝，工程存在较严重安全隐患，不能按设计正常运行。参考文献[7]将大坝运行风险度分为四个等级，相应的评语依次为N1（微风险）、N2（低风险）、N3（中风险）和N4（高风险），其中取一类坝中的20%划归为“微风险”，其余的划归为“低风险”；将二类坝全部划归为“中风险”；将三类坝全部划归为“高风险”。

各类事件的先验概率P(Ni)可以通过我国水利系统现有的大坝安全分类统计情况进行确定，表1统计的为某一年水利系统80 427座大坝安全分类情况[7]。

表1 某年全国水利系统水库大坝安全分类Table 1 Safety classification of reservoir dams in China's water conservancy system in a given year

通过计算P(N1)=0.06，P(N2)=0.25，P(N3)=0.33，P(N4)=0.36。取大坝运行风险度值区间为[0,1]，则根据各类事件的先验概率，可以确定各风险等级对应的大坝运行风险度区间如下：

式（2）表示若某一风险因素的风险度值在[0,0.06]区间时，该因素的特性为“微风险”，以此类推。当计算出风险因素的风险度值，即可通过评价体系自下而上逐层确定大坝运行的综合风险度。

3 基于实测资料的大坝运行风险度分析

大坝是一个由不同部位组合而成的复杂体系，其综合运行风险度实质上是多个组成部位风险度的综合反映。各个部位的风险度可通过不同项目各个测点的实测资料分析得到，因此大坝综合运行风险度确定的过程可分解为大坝运行单项、局部和综合风险度分析。

文献[7]通过数值趋势和时效趋势两方面建立了单个测点的单项运行风险度，具体计算方法如下。

图2为单测点单项测值风险度的评价级别划分方案，图中，y为效应量的实测值，如变形、渗流等；y为根据监控模型求得的效应量的拟合值，y=f(x)，x指影响效应量的自变量因子；S为监控模型的均方差；ymax、ymin为拟定的安全阈值上限值和下限值，但对于有些效应量（如渗流量等），没有下限值。

图2中，把大坝效应量测值y分为4个区域，如下式：

时效分量可以充分反映大坝结构风险的变化趋势，图3为单测点测值风险度趋势表现的评价级别划分方案，图中将测值的时效分量划分为4种形式：

图2 单测点测值风险度数值表现评价级别划分Fig.2 Single point operation risk division by numerical performance

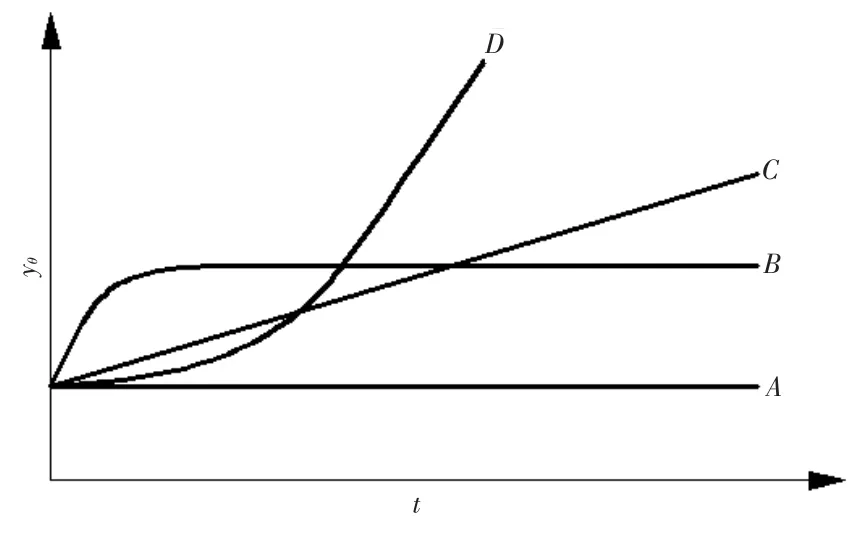
图3 单测点测值风险度趋势表现评价级别划分Fig.3 Single point operation risk division by trend performance

（2）时效分量初期增长较快，后期趋于稳定，如曲线B所示，。这种情况最为常见，表示大坝的运行情况良好，与之对应的风险度评估等级为“低风险N2”。

式（3）中，A、B、C、D区分别对应该测点测值风险P1特性为微风险、低风险、中风险和高风险，图3中，A、B、C、D四条趋势线分别对应该测点趋势风险P2特性为微风险、低风险、中风险和高风险。根据不同项目，不同测点的实测数据和上述划分准则，可以建立一个模糊的单因素评价向量R：

式中：rij为该风险元素Pi对评价向量Nj的模糊隶属度，其中，r1j等于落在各个区间内的测值个数占总测值个数的比。当测点的时效分量与相应于图3中某一条曲线Nj变化一致时，r2j=1，而取r2k=0（k≠j）；当测点的时效分量介于相应于Nj和Nk的两种曲线之间时，取r2j＞0，r2k＞0且r2j+r2k=1，其余r2m=0（m≠j,k）。

为了获得数值表现和趋势表现的综合风险度，需要构造两者的权重向量W=[ω1ω2]，权重向量的取值根据专家经验确定，最后得到测值综合评价指标向量Z：

根据模糊隶属向量Z，可根据式（6）计算该测值的风险度：

式中：RIE为某风险因素的单项风险度；zi为该风险因素模糊隶属向量Z中的第i个级别对应的模糊隶属度；ai、bi分别为zi对应的风险等级所属区间的下限和上限。

在确定了大坝的全部单项风险度值之后，可以根据文献[7]给出的公式计算大坝局部运行风险度RIB和大坝综合运行风险度RI。

4 基于Markov链的大坝时变风险度模型构建

4.1 Markov基本理论

若当前随机变量取值是通过它的前一个变量决定，而与其之后的变量无关，则该随机过程称为马尔科夫过程。随着马尔科夫理论的完善与推广，目前已被广泛用于城市人口、水质分析、语音和人脸识别等众多领域的预测研究中[8-10]。

一个时间与空间都是离散的马尔科夫过程叫做马尔科夫链[11]。离散的马尔科夫链用数学语言可表达如下：

设一随机过程{Xt,t≥ 0}，如果Xt∈S(t=1,2,···)，其中S为一有限集合的状态空间，且对于任意的i，j，i0，i1，···，in+1，S都有：

式中：i，j，i0，i1，…，in+1为系统所处的状态；P为转移概率矩阵；t为时间；X为离散的马尔科夫链。

马尔科夫链最重要且最基本变量是转移概率矩阵P，其表达式如下：

式中：Pij(t)表示当系统t时刻处于i状态时，系统t+1时刻处于j状态的概率，；m为系统所具有的状态个数。

齐次马尔科夫链的状态矩阵与时间无关，系统任一时刻的所处状态均可根据式（9）求得：

式中：Xt为系统在时间t所处的状态；X0为系统的初始状态。

4.2 转移概率矩阵的确定

转移概率矩阵是马尔科夫链模型最核心的部分，目前常用的确定转移概率矩阵的方法有经验判断法、统计分析法、回归分析法和基于逆阵的方法[12]。除了经验判断法之外，剩余三种方法对监测数据的要求均较高，计算工作量也较大，因此，为了简化计算工作，通常需要做出某些合理的假定条件，从而简化转移概率矩阵。

结合工程结构实际情况，做如下假定：（1）在正常运行条件下，不考虑除险加固措施影响，结构在寿命周期内的转移概率不变；（2）结构任意时刻所处的风险等级只有两种情况，维持当前风险等级状态和向更高风险等级状态转移。假定（1）认为结构的运行风险度在寿命期内连续均匀变化，这一假定不考虑转移概率矩阵与时间的关系，故建立的马尔科夫链为齐次的，可以大大减少计算工作量。假定（2）认为结构只能朝更高风险等级发展，由于不考虑除险加固的影响，大坝的性能随时间将逐渐劣化。基于上述假定条件的马尔科夫链如图4所示。

图4 大坝运行风险的马尔科夫链模型Fig.4 Dam operation risk model based on Markov chain

由此可得转移概率矩阵为

式中：Px为大坝结构运行风险从当前状态向下一状态转移的概率。

由式（10）可以看出，简化后的概率矩阵只含有一个未知数Px，如果已知t1、t2（t2＞t1）时刻大坝运行风险状态的分布向量Xt1、Xt2，则根据式（11）可以反求出变量Px，进而计算状态转移矩阵P。

4.3 大坝运行风险度转异判据

根据大坝运行风险度确定大坝工程从正常转为异常的征兆是一个涉及多方面的复杂技术问题。在水利工程结构运行风险度分析的基础上，结合现有规范，尝试建立大坝运行风险度转异判据。

大坝运行风险度评判准则将大坝运行风险度分为4个等级，各运行风险度等级对应的运行风险度值见表2。

表2 大坝运行风险度等级划分表Table 2 Dam operation risk classification

根据《水利大坝安全鉴定办法》，初建大坝运行风险度转异判据如下：

（1）当RI≤0.31时，对应《水利大坝安全鉴定办法》，该大坝处于“一类坝”，认为大坝运行正常，只需采取日常维护措施即可；

（2）当0.31＜RI≤0.64时，对应《水利大坝安全鉴定办法》，该大坝处于“二类坝”，认为大坝从正常转为带“病”运行，此时大坝需要进行维修处理；

（3）当RI＞0.64时，对应《水利大坝安全鉴定办法》，该大坝处于“三类坝”，认为大坝由“病坝”转异为“险坝”，此时需要对大坝进行加固处理。

实际运行情况中，当某一大坝被判定为“三类坝”时，经过除险加固后大坝还能够运行。吴中如[7]将三类坝的80%划归为高风险，剩余的20%划归为恶性风险，即高风险对应的运行风险度区间为（0.64,0.93]，恶性风险对应的运行风险度区间为（0.93,1.00]，因此，认为当大坝的运行风险度RI＞0.93时，大坝处于风险度极高的状态，不适宜继续运行。

4.4 大坝运行风险度转异诊断过程

不考虑除险加固效应的大坝运行风险度转异诊断基本步骤如下：

（1）选取若干段大坝原型监测资料，一般以每5年的监测资料为一个评估时段；

（2）根据大坝原型监测资料建立统计模型，并分离时效分量；

（3）拟定大坝安全阈值，计算大坝单项、局部和综合运行风险度；

（4）根据大坝单项运行风险度，由式（11）计算状态转移矩阵P，建立单项运行风险时变模型，进而建立局部运行风险度和综合运行风险度时变模型；

（5）根据大坝综合运行风险度时变模型以及大坝运行风险度转异判据，评估大坝在全寿命周期内的风险度等级。

5 实例分析

以某混凝土大坝为例，分析该坝的运行风险度和运行寿命。该混凝土坝位于第二松花江干流上，于1937年修建，1951～1953年进行了扩建和改建，1953年全部建成。枢纽工程由混凝土重力坝、溢流坝、坝后式厂房及变电站、左岸泄洪洞（后改建成三期引水洞）及三期发电厂房组成。拦河坝最大坝高91.7 m，坝顶长度1 080 m，坝顶高程267.70 m，共有60个坝段。目前电站总装机容量为1 002.5 MW，多年平均发电量19.68×108kW·h。水库正常蓄水位263.50 m，汛限水位260.50 m，死水位242.00 m，校核洪水位267.70 m，总库容109.88×108m3，为多年调节水库。

5.1 大坝运行风险辨识

初步确定影响大坝运行的风险因素主要包括变形、强度、老化、渗流等，如图5所示。

图5 某大坝运行风险评价粗集Fig.5 Rough set of operation risk assessment for a dam

参考类似工程，相应于图5的四个判断矩阵为：

采用文献[13]的方法对大坝运行风险因子进行权值排序，计算结果见表3。

从表3得到的各风险因素总排序权值来看，影响该大坝安全运行的风险因素主要包括坝体变形（ω1=0.416）、坝体强度（ω3=0.170）和坝基渗流（ω3=0.169）。

5.2 基于实测资料的大坝运行风险度计算分析

根据该大坝的实际情况，其安全监控重点坝段包括14号、22号和35号坝段，其中，14号坝段坝基存在断层，破碎带宽度超过5 m，此外还存在坝顶向上游时效变形、坝顶上抬较明显、坝体裂缝较严重等问题；22号坝段存在坝基扬压力大、坝基漏水量较大、坝体混凝土质量较差等问题；35号坝段是该大坝监控的核心坝段，其重要性远大于其他坝段，而35号坝段处于坝址区最大的断层破碎带中心区域上，建基面物理力学参数偏低，抗滑承载力不足，坝基稳定安全系数低，此外，35号坝段还存在坝顶位移大、坝顶向上游时效变形、坝体混凝土强度低、坝基扬压力大等问题。

表3 某大坝运行风险因素总排序权值计算结果Table 3 Weights of operation risk factors for a dam

根据运行风险辨识的结果和重点坝段存在的问题，收集如下实测数据资料用于建模分析：（1）14号坝段坝顶垂直位移y1、坝基渗漏量y2资料；（2）22号坝段的坝基渗漏量y3、坝基扬压力y4资料；（3）35号坝段的坝顶水平位移y5、坝体渗漏量y6、坝基横向扬压力y7资料。根据各测点2001年1月～2010年9月的观测数据，建立统计模型并分离时效分量。风险度计算第一个评价时段选取2001～2005年的监测资料，第二个评价时段选取2006～2010年的监测资料。数值表现和趋势表现的权重向量W=[0.7,0.3]，2001～2005年大坝单项、局部运行风险度计算结果见表4，2006～2010年大坝单项、局部运行风险度计算结果见表5。

由大坝的局部运行风险度计算公式可以计算大坝综合运行风险度，其中2001～2005年大坝综合运行风险度为0.494，大坝处于“中风险”状态。2006～2010年大坝综合运行风险度为0.634，大坝处于“中风险”状态。

表4 2001～2005年某大坝单项、局部运行风险度计算结果Table 4 Calculation results of single and local operation risk degree from 2001 to 2005

表5 2006～2010年某大坝运行单项、局部风险度计算结果Table 5 Calculation results of single and local operation risk degree from 2006 to 2010

现计算各因素综合模糊向量的Markov状态转移矩阵，由上述两个时段综合模糊隶属向量和式（11）可计算大坝各因素结构运行风险从当前状态向下一状态转移的概率Px，见表6。

由状态转移矩阵Px，可计算任意时刻该大坝的综合模糊隶属向量，从而可计算任意时刻该大坝的单项、局部和综合运行风险度。其中，各因素单项运行风险度时变图见图6，各坝段局部运行风险度时变图见图7，大坝综合运行风险度见图8。由图8可以看出，该大坝再运行8年之后（2013年）将处于高风险状态，有必要进行除险加固处理，若不考虑除险加固效应，该大坝在第34年后处于恶性风险状态，大坝不适宜继续服役。