水库防渗措施及坝后排水沟距离对周边农田地下水埋深的影响

张才军

(湖北省漳河土木工程设计院，湖北 荆门 448000)

水库渗漏对于水库安全有着不可忽视的影响，其能够抬高水库四周地下水水位，也能够影响水库坝体的安全稳定[1- 4]；同时由于地域的限制，在干旱及半干旱的气候变化下，渗漏问题将会带来一系列的连锁反应，譬如水库蓄水量不足、影响农业的可持续发展等[5- 8]。为了改善此类问题带来的负面影响，工程界采用了“上防下排”的措施，即在水库及坝体采用防渗措施，同时在坝后采用排水措施。

本文通过有限元软件，对某水库工程进行计算、分析，研究不同防渗措施、坝后排水沟距坝趾距离及深度对地下水埋深的影响，结合渗流理论计算水库的抗滑稳定性，为该类水库工程的防渗措施提供相应的理论基础。

1 理论基础

1.1 渗流理论

土体保持非饱和状态，其基质吸力与土体含水率和渗透系数相关，主要决定性因素为孔隙水压力和孔隙气压力。土水特征曲线是非饱和状态下的土体含水率与基质吸力之间的关系曲线；而非饱和渗流方程，故为非饱和状态下土体的渗透系数与基质吸力之间的方程。在实际工程中，Van Genuchten的非饱和状态下土水特征曲线以及渗流方程应用更为广泛。

非饱和土水特征曲线方程的具体公式为：

μm=μα-μw

(1)

式中，μm、μα、μw—基质吸力、孔隙气压力和孔隙水压力；kPa；θw、θs和θr—体积含水率、饱和含水率和土体残余体积含水率；αw—与进气值相关的参数；nw—反映体积含水率变化速率的参数；nw—非饱和土残余状态相关的参数，计算公式为：

(2)

渗流方程公式为：

(3)

式中，k、ks—土体渗透系数和土体饱和渗透系数，其中土体饱和渗透系数与土体孔隙水压力有关系，具体关系式如下：

(4)

式中，ks0—土体初始饱和渗透系数；n、n0—土体的孔隙率以及土体初始孔隙率。

1.2 坝体抗滑稳定性

坝体抗滑稳定性计算通过条分法计算，计算公式如下：

(5)

式中，F—坝体抗滑稳定安全系数；li—第i块在滑弧上的长度；φi、ci—第i块的土体材料内摩擦角和粘聚力大小；σni—第i块滑块在圆弧滑面上的法向应力；τi—第i块滑块在圆弧滑面上的切向应力。

2 数值计算

2.1 模型建立

本次数值计算采用的工程原型为新疆某水库工程，典型断面如图1所示。其中坝基面水平高程采用869.00m，坝顶高程877.30m，水库正常设计水位875.00m，水库坝顶宽度为6.00m，水库坝体上、下游的坝坡坡比均为1∶2.5，水库坝基的防渗体均采用土工膜水平铺设，其铺设长度是坝前水头的22倍，即132m。S为排水沟距离坝趾长度，m；h2为排水沟深度，m。

图1 模型典型断面图

该水库在原断面的基础上，进一步增加防渗措施，即水平铺盖和悬挂式防渗墙，具体位置如图2所示，防渗墙的厚度0.4m，防渗墙长度为20.00m。其余坝体尺寸保持相同。

图2 防渗措施模型图

2.2 模型参数

数值模拟选取的模型参数均通过实际测量及勘察得到，具体材料参数见表1。

表1 材料参数

2.3 试验方案

数值模拟将通过有限元软件对不同试验方案进行计算，主要针对防渗措施以及坝后排水沟对地下水位的影响，设计计算方案见表2。

表2 试验方案

注：计算1组、2组和3组分别对排水沟与坝趾距离和深度进行排列组合，即每组试验进行9个有限元试验计算。

3 计算结果

S=100m时地下水埋深计算结果如图3所示，由图3可知，排水沟距坝趾的距离及排水沟的深度对地下水埋深影响较大；当排水沟深度不变时，地下水深出现先减小后增大，最后在排水沟后缘一定范围内保持地下水埋深不变，在排水沟底部出现地下水最大埋深；当排水沟距坝趾的距离不变时，随着排水沟深度的增加，最大地下水埋深也逐渐增加，最后稳定的地下水埋深相应增加；对比排水沟前后的地下水埋深可知，排水沟能够消耗一定的水头，进而使经过排水沟后的地下水埋深增加。

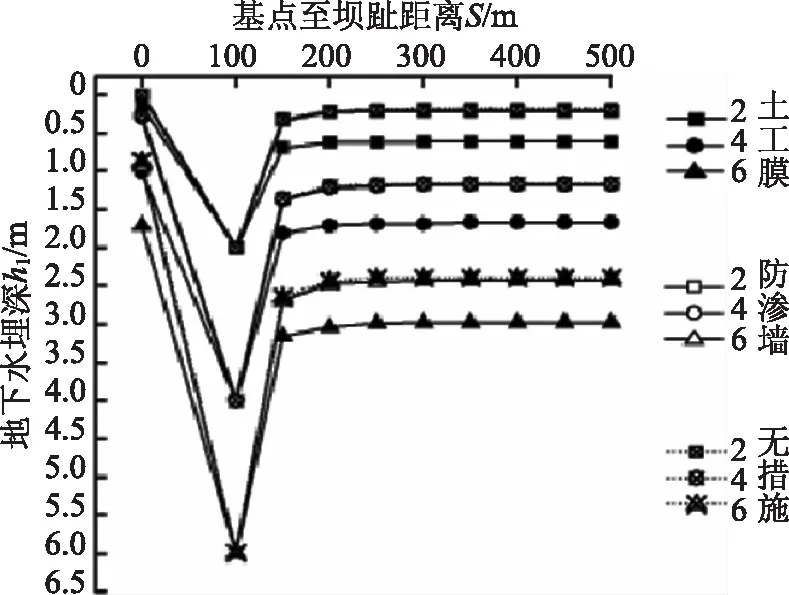
图3 S=100m时地下水埋深计算结果

3.1 排水沟位置对地下水的影响

h2=2m时不同坝趾距离地下水埋深计算结果如图4所示，由图4可知，当坝体没有防渗措施及排水沟深度一定时，地下水埋深随着排水沟距坝趾距离的增加而先降低后增加；当有防渗措施(防渗墙和土工膜)时，地下水埋深随着排水沟距坝趾距离的增加而增加，由于坝前水头有限，在无防渗措施时，其影响范围可能在本次计算范围内；当有防渗措施时，坝前水头在防渗措施作用下得到一定的削弱，进而使其影响范围减小，并小于本次计算范围，导致其地下水埋深逐渐增加。

图4 h2=2m时不同坝趾距离地下水埋深计算结果

h2=4m时不同坝趾距离地下水埋深计算结果如图5所示，由图5可知，地下水埋深的变化规律与图4保持相同，即两者的原理基本相同。

图5 h2=4m时不同坝趾距离地下水埋深计算结果

h2=6m时不同坝趾距离地下水埋深计算结果如图6所示，由图6可知，当坝体排水沟深度一定时，在不同防渗措施下，地下水埋深随着排水沟距坝趾距离的增加先降低后增加；主要是因为其排水沟深度的增加，相当于增加了坝前水头与排水沟的水头差，在有防渗措施情况下的水头影响范围也逐渐增加到本次计算范围内。

图6 h2=6m时不同坝趾距离地下水埋深计算结果

3.2 排水沟深度对地下水的影响

S=60m时不同坝趾距离地下水埋深计算结果如图7所示，由图7可知，当排水沟距坝趾的距离不变时，随着排水沟深度的增加，地下水埋深也不断增加；当有防渗措施时，其变化规律也相同；而对坝体使用土工膜比防渗墙的地下水埋深更大。可能是由于随着排水沟深度的增加，进而增加对地下水水头的损失，使地下水埋深进一步增加；土工膜比防渗墙产生的地下水埋深更大，是因为土工膜的防渗效果较防渗墙好。但随着排水沟深度的增加，两种防渗措施产生的地下水埋深越来越接近。

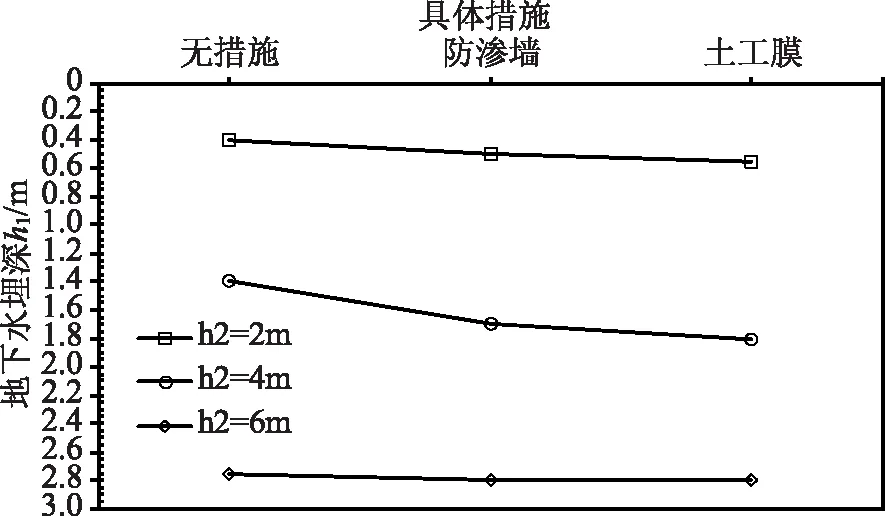
图7 S=60m时不同措施下地下水埋深计算结果

S=100m时不同坝趾距离地下水埋深计算结果如图8所示，由图8可知，随着排水沟深度的增加，地下水埋深的变化规律与图7基本保持相同，即两者之间的原理也基本相同。

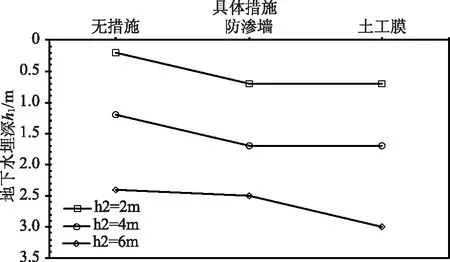
图8 S=100m时不同措施下地下水埋深计算结果

S=140m时不同坝趾距离地下水埋深计算结果如图9所示，由图9可知，当排水沟距坝趾的距离达到一定时，不同的防渗措施产生的地下水埋深基本相同，即防渗措施虽然有作用，但不同的防渗措施效果所达到的效果基本相同。主要原因是随着排水沟距坝趾的距离达到一定时，在无防渗措施时其坝前水头所影响的范围能够达到，但是当有防渗措施时，其影响的范围达不到，所以两者的影响效果相同。

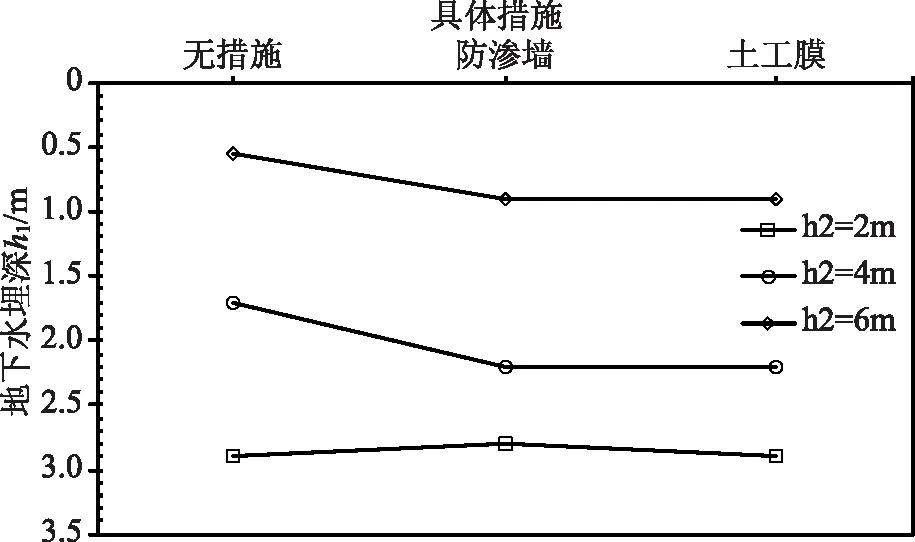
图9 S=140m时不同措施下地下水埋深计算结果

3.3 下游坝坡稳定性分析

h2=2m时不同坝趾距离下安全系数(抗滑安全系数，本文视为安全系数)计算结果如图10所示，由图10可知，在排水沟深度一定时，无防渗措施坝体的安全系数相比有防渗措施坝体安全系数较低，具有土工膜防渗措施的坝体安全系数最大；并且随着排水沟距坝趾距离的增加，所有方案下的坝体安全系数均出现逐渐增加的趋势。主要原因是防渗效果越好，地下水埋深相对越大，对坝体安全影响越小；随着排水沟距坝趾距离的增加，地下水埋深也逐渐增加，所以对坝体的安全影响减小。

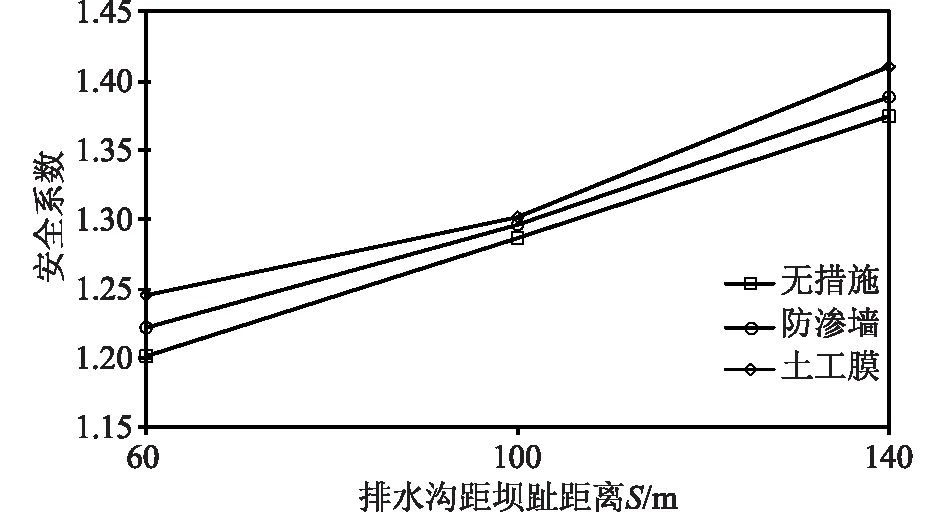
图10 h2=2m时不同坝趾距离下安全系数计算结果

S=60m时不同措施下安全系数计算结果如图11所示，由图11可知，在排水沟距坝趾的距离一定时，不同防渗措施下，随着排水沟深度的增加，坝体的安全系数逐渐增加，主要是因为随着排水沟深度的增加，地下水埋深也不断增加，进而对坝体安全系数的影响越小；当排水沟深度达到一定时，坝体使用不同的防渗措施，其安全系数基本相同，主要是因为当排水沟深度达到一定时，不同的防渗措施产生的地下水埋深基本相同，进而使其安全系数基本相同。

图11 S=60m时不同措施下安全系数计算结果

4 结论

通过有限元数值模拟计算坝体在不同防渗措施、坝后排水沟距坝趾的距离以及排水沟深度对地下水埋深和坝体安全的影响，并得到以下结论：

(1)在排水沟深度和距坝趾的距离一定时，坝体采用防渗措施将有效的增加地下水埋深；且土工膜防渗措施比防渗墙防渗措施产生的地下水埋深更深。

(2)当坝体有、无防渗措施时，地下水埋深变化规律不同，前者随着排水沟距坝趾距离以及排水沟深度的增加而逐渐增加，后者随着排水沟距坝趾距离的增加先降低后增加，随着排水沟深度的增加，地下水位也增加。

(3)有防渗措施坝体稳定性更高，采用土工膜防渗措施的坝体稳定性最好；随着排水沟距坝趾距离以及排水沟深度的增加，坝体安全系数逐渐增加；当排水沟深度达到一定时，坝体使用不同的防渗措施，对坝体稳定性影响较小。