农田水利工程灌溉效果综合评价研究
2019-01-16贺建宇
贺建宇
(大宁县水利局,山西 大宁 042300)
现有灌区的农田水利工程存在建设时间长、配套设施弱、质量管理措施落后等缺点。20世纪90年代以来,国家开始出台相关政策,大力推进农田水利工程的建设[1- 2]。我国是农业大国,农业的发展离不开农田水利工程建设[3- 5]。对于农田水利工程的设计,我们应根据当地的实际需要,推广最新的节水灌溉技术,发展绿色节水农业,与国家可持续发展目标对接[6]。目前国内研究尚未从灌溉效果角度,明确农田水利工程建设的实际效益,本文以山西省大宁县农田水利工程为例,列出农田水利工程的具体设计方案,以期为农田水利工程设计提供依据,通过综合比较农田水利工程建设前后的灌溉效果,更直观地反映农田水利工程建设的必要性。
1 农田水利工程建设地基本情况
大宁县总面积967.13km2,区内气候属暖温带半干旱大陆性气候,年均气温为11.1℃,极端最低气温-20℃,极端最高气温38.7℃,多年平均降水515mm,最高年降水794.7mm,最低年降水280.2mm,日照时数2466.7h,无霜期213d,多年平均水面蒸发量996.7mm,干旱指数1.9。灌区0.38万亩,小型泵站灌区3.0471万亩。全县农田水利工程运行费投入不足,农民收入低,集体经济薄弱,加上农村税费制度的改革,使得早年建设的小型自流工程老化失修,不能发挥灌溉效益。目前的管理办法不能保证工程持续发展。
2 农田水利工程设计
以山西省大宁县滴灌工程为例,地块总面积为400亩,根据实际调查,400亩地块分散为两部分,分别为258亩及142亩(以下以系统A和系统B进行区分),种植作物为蔬菜。根据GB/T 50485—2009《微灌工程技术规范》,设计滴灌灌水定额mmax为:
mmax=0.001γzp(θmax-θmin)=0.001×45×36×(28-15)=21.049(mm)
(1)
式中,mmax—最大净灌水定额,mm;γ—土壤容重,g/cm3;z—土壤计划湿润土层深度,m,取0.45m;p—微灌土壤湿润比,根据实际情况,取35%;θmax—适宜土壤含水率上限(重量百分比),%;θmin—适宜土壤含水率下限(重量百分比),%。
根据灌水临界期作物最大日需水量值,按式(1)计算理论灌水周期。因为,实际灌水中可能会出现停水、配水设备故障等原因,故设计灌水周期应小于理论灌溉周期,根据式(2)可算得灌水周期为:
T理=mmax/ETc>T设=23.39∕4.5=5.20d
(2)
式中,T理—理论灌水周期,d;ETc—需水量,根据相关规范及当地种植经验,取4.5mm/d;T设—设计灌水周期,d。
系统A,系统B均按照地形条件分为10个大小相当的小区,每个小区分为1个轮灌组,共10个轮灌组。由于滴灌周期计算结果为5d,每2小区即可按照1d的时间进行规划,每个轮灌组一次灌溉用时8h。根据地形和植被种植模式,将高程相近、地块毗邻、面积相似的小区划作一个轮灌组,具体轮灌组划分见表1。
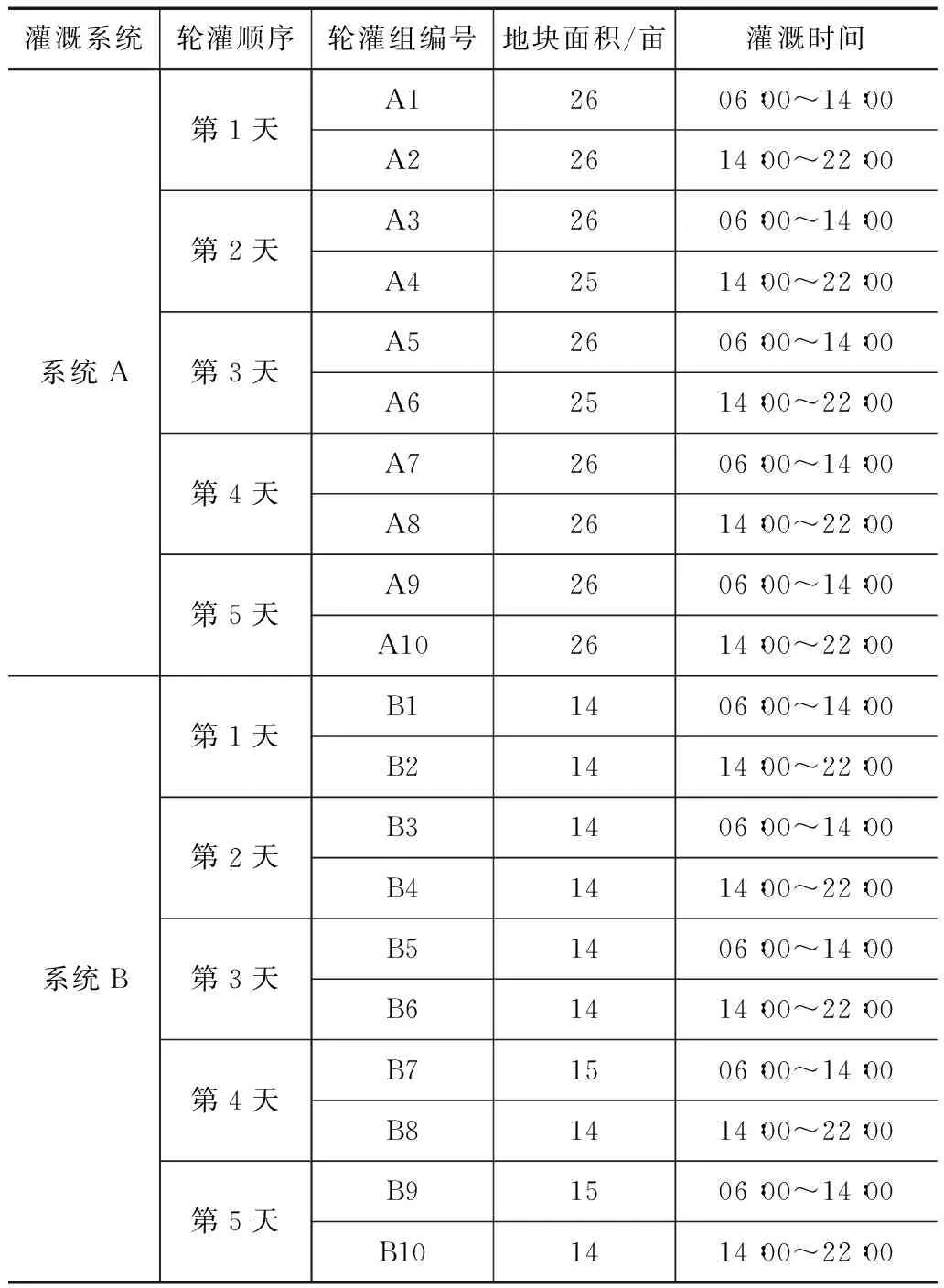
表1 轮灌组分区表
综合考虑不同材料管材的价格、脆塑性、购买和安装便利性以及地方实际情况,本项目用于系统管网的管材干支管均选用PE管,压力校核时,为了方便采购及安装,所有干管所选用的压力等级均一致,最终校核结果干管压力采用1.0MPa,支管同样的校核原理,校核结果为0.8MPa。
在干支管管径计算上,采用下列经验公式进行分析计算:
当Q>120m3/h时
D=11.5×Q1/2
(3)
当Q≤120m3/h时
D=13×Q1/2
(4)
式中,D—计算管径,mm;Q—管道设计流量,m3/h。
3 农田水利工程灌溉效果评价
3.1 评价指标体系构建及评价方法
本文选取农田水利工程建成前后2年,即建成前2012、2013,建成后2016、2017年的统计数据,在经济、社会和生态3个层面,综合比较建成前后的灌溉效果,可较全面的反映农田水利工程建设对当地的影响。由于综合评价法存在主观性和客观性[7],为使得评价方法兼顾事实的客观性和专家的主观性,本文基于反映主观性的层次分析法[8]和反映客观的熵权法[9],并结合灰色关联度分析法[10]形成新型的综合评价方法,对不同指标进行打分,最后形成不同年份灌溉效果的综合得分情况,具体方法见文献[10]。该方法可较全面地反映灌溉效果。同时,从经济、社会和生态3个方面,共选取12项指标,综合判定灌溉效果。综合评价指标体系构建如图1所示。
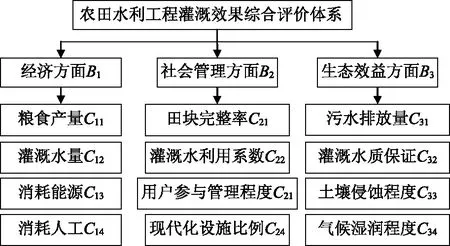
图1 农田水利工程灌溉效果综合评价指标体系构建
3.2 灌溉效果综合评价结果分析
综合分析农田水利工程建成前后的2012、2013年和2016、2017年的实测数据,依据层次分析法的原理,并根据经济、社会管理方面和生态效益方面不同指标的重要性,得到第二层指标的判断矩阵,从而计算得出第二层指标的权重,结果见表2。以经济方面指标为例,算得其判断矩阵见表3,可算出其所在第三层各指标的权重,以此类推,可算出其余两个方面各指标的最终权重,结果见表4。
根据表2中的数据,可得出第二层指标的权重,根据表4的数据,可得出第三层指标的初始权重,综合两方面数据,可得出第三层指标的最终权重,得出了灌溉效果评价的主观权重,结果见表5。
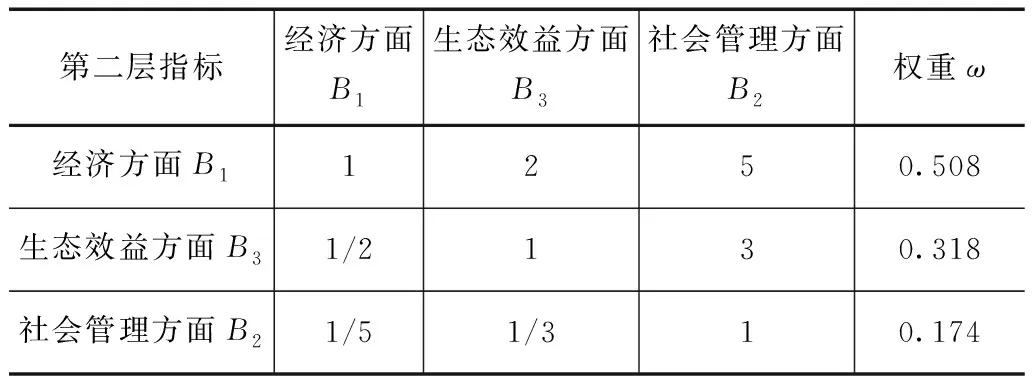
表2 第二层指标层次分析法判断矩阵
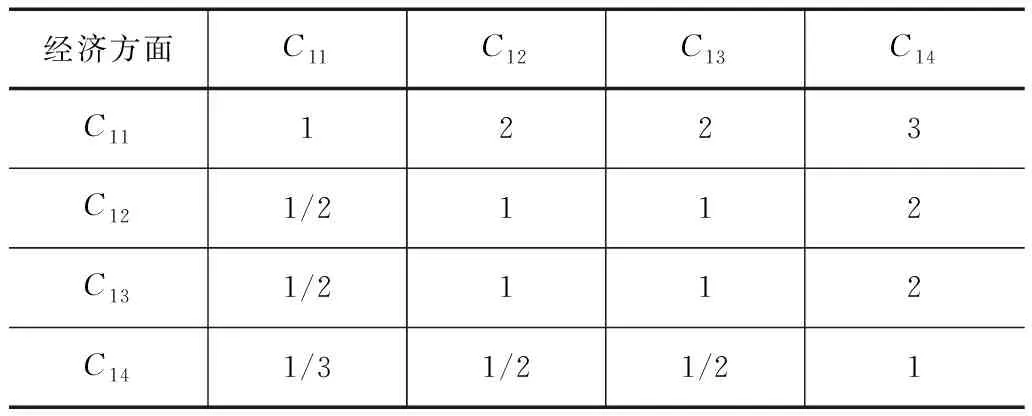
表3 经济方面指标判断矩阵
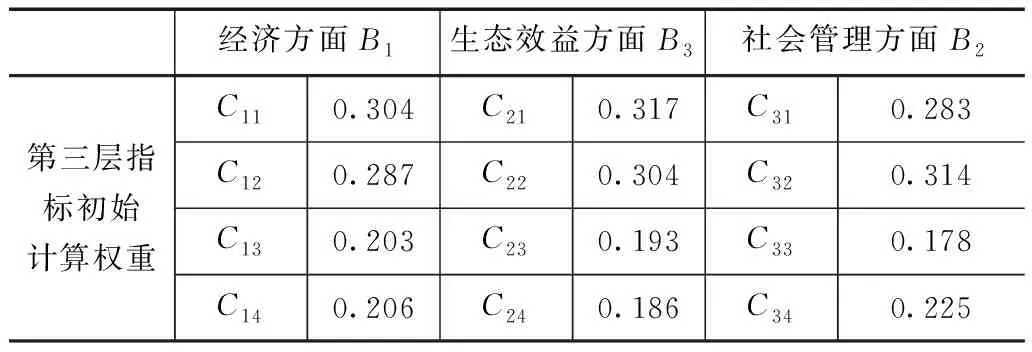
表4 第三层指标权重
根据文献[8]计算不同指标的相对隶属度矩阵,从而可得出熵权法第三层指标的客观权重,根据表5中由层次分析法计算得出的主观权重,最终可得出第三层指标的最终权重,结果见表6。
根据文献[11]计算第三层指标的关联系数,结果见表6。根据表6中的最终综合权重,对表7中的数据进行综合加权,得出每一年不同指标的综合加权关联系数,结果见表8。
根据表8中的结果,可知不同年份的灌溉效果综合排名。表8显示,不同年份综合排名由高到低依次为2017、2016、2013、2012年。由此可知,在建设农田水利工程前,当地灌溉效果较差,但在建成工程之后的2016、2017年,灌溉效果有了明显提高,这与实际情况相符,验证了该方法的准确性,也从数据角度反映了农田水利工程的效果。
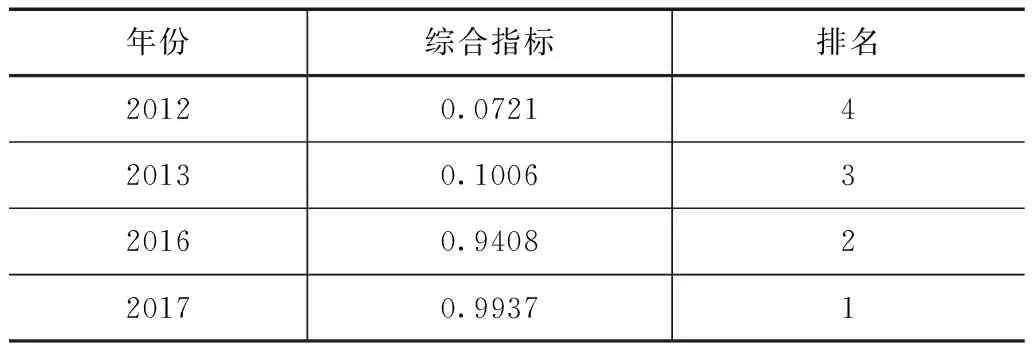
表8 不同年份灌溉效果综合排名
4 结论
在验证不同年份内,农田水利工程的建设对当地灌溉效果的影响时,指出了不同年份灌溉效果综合排名由高到低依次为2017、2016、2013和2012年,2017年的灌溉效果最佳。

表5 第三层指标层次分析法主观权重

表6 第三层指标最终权重确定

表7 第三层指标灰色关联系数
