大体积混凝土温度变化及有限元数值模拟

2019-01-16郭生根

水利规划与设计 2018年12期

郭生根

(江西省港航管理局，江西南昌 330023)

混凝土结构在实际使用过程中承受各种各样的外荷载和变形荷载[1]。其中静、动荷载等被称为第一类荷载，而变形荷载被称为第二类荷载。第一类荷载所产生的裂缝可按常规计算得出；第二类荷载产生的裂缝原因是当结构变形得不到满足时，产生应力形成裂缝[2]。因此，对第一类荷载所产生的裂缝可以通过设计来得以控制；而第二类荷载所形成的裂缝影响因素较为繁多，其中温度应力是主要因素[3]。

国内外已经有不少专家学者对这类问题开展了研究，吴峰等二次开发ANSYS对混凝土结构的温度裂缝控制进行了分析[4]；张子明等采用裂缝带模型计算温度裂缝[5]；刘杏红等采用无网格方法对混凝土的温度裂缝过程进行了仿真计算[6]；陈辉等利用大型有限元分析软件ANSYS中的三维实体单元对混凝土梁进行了热固耦合分析[7]；贾福杰建立的半绝热温升试验-有限元分析计算模型，其误差可控制在10%以内[8]。

由于混凝土水化热的散发，气温、水位、水温、日照等外界条件的变化都是时间的函数，这些因素决定了混凝土在第二类荷载作用下裂缝形成的复杂性[9]。因此，本文采用COMSOL有限元软件进行分析。

1 COMSOL仿真模拟

1.1 热固方程

传热方程可表示为[10]：

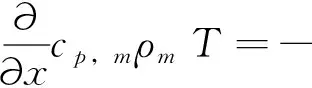
(1)

导热热流密度可以通过傅里叶定律来表示：

q=-λT

(2)

式中，λ—导热系数，W/(m·K)；方程右边的负号表明热流密度方向与温度梯度方向相反；ρm—干材料密度，kg/m3；cp，m—干材料的比热，J/(kg·K)；

因此在三维状态下，可表示为[11]：

(3)

将式(3)简化后，得到固体介质中的热传导方程：

(4)

混凝土结构底部处为固定约束，从而会形成热固耦合，如式(5)。

σi，j=2Gεi，j+(Ae-βT)δi，j

(5)

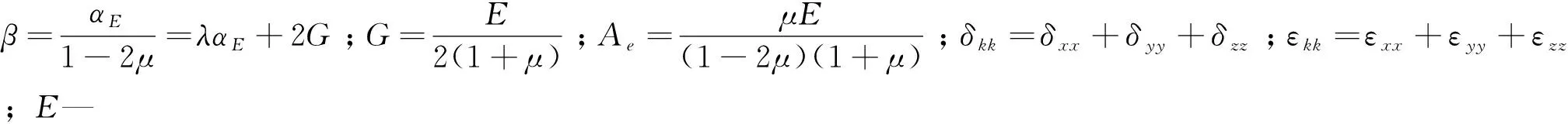
1.2 建立模型与材料参数

以工程实例为基础建立三维有限元模型，尺寸为80m×36.1m×2.5m。大体积混凝土选用P.O.42.5级水泥，其28d后的抗压强度为51MPa。考虑到混凝土主要受到温度的影响，其具体参数见表1。

表1 材料的基本参数

1.3 网格划分及其精确性

采用COMSOL自带的网格划分功能，并选用细化网格：最大单元尺寸为1.6m，最小单元尺寸为0.016m；最大单元生长率为1.3，其曲率因子为0.2；狭窄区域解析度为1；利用该参数划分网格，并进行网格独立性检验，如图1所示。从图1中可以看出，网格划分完好，在有限元分析计算中可以得到较为精准的结果。

1.4 边界条件的确定

(1)通常混凝土在9月底进行浇筑，因此假设混凝土浇筑温度设置为30℃。左右两侧设置为开放边界条件，并且考虑热固耦合将四周及底部设置为固定约束。为了得到最佳施工期，结合COMSOL参数化扫描，将环境温度设置为变量T1(其范围为0～60℃)；并计算混凝土的最大应力变化。根据试验资料，水泥累计水化热一般用式(6)计算。

Qt=Q0(1-e-mt)

(6)

式中，Qt—在龄期t时的累计水化热，KJ/kg;Q0—水泥水化热总量，KJ/kg；m—常数；t—龄期。

(2)当环境温度为30℃恒定时，求得混凝土中心点和表层温度的变化规律；得出在不同厚度的监测点温度变化，其余条件如上所述。

(3)同时考虑浇筑温度的影响，将混凝土的初始温度设置为变量T2(其范围为20～40℃)，而环境温度20℃保持不变，其余条件如上所述。

2 讨论

2.1 模拟最佳施工周期

大体积混凝土浇筑1h后，计算其内部最大拉应力，如图2所示。当外界环境温度与混凝土浇筑温度相差较近时，其内部初始最大拉应力则最小；这是因为温度差越小时，所产生的温度梯度越小，从而导致温度应力减少。从这一结果可以看出，为了减少混凝土裂缝的产生，首先应该选取合适的施工期，避免浇筑时大体积混凝土就出现裂缝情况。其次，水泥水化热随时间变化，应充分监测到水泥水化放热的最大值。

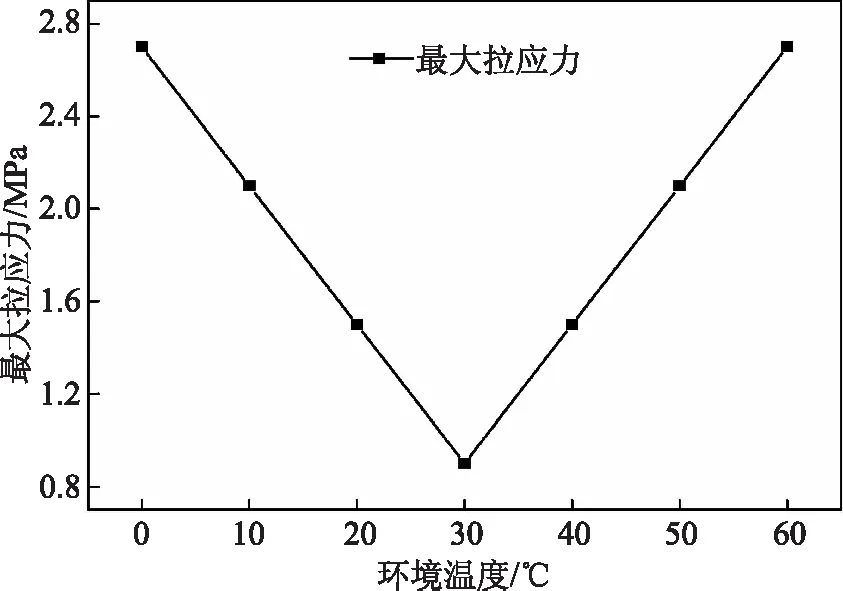
图2 最大拉应力随环境温度的变化曲线

2.2 监测点的温度变化

表面、中间两监测点温度随时间的变化如图3所示，从图3可以看出，中间处温度时，实测温度比模拟温度偏低，且较为吻合；在表面监测点处模拟与实测数据误差较大，这是因为在实际工程中环境因素较为复杂，如在表面处还会存在热对流、热辐射现象，从而加快温度耗散；而中间处监测点，可假定大体积混凝土为一维热传导，其受到外界影响较小。

在前120h时，水泥水化放热和外界环境的热传导使得大体积混凝土内部温度上升；而之后大体积混凝土温度逐渐下降，达到与外界温度相一致。从实测数据可知，中间温度与表面温度最大可达到约30℃，因此，为了避免大体积混凝土内部温差较大产生裂缝，应采取冷水管使大体积混凝土降温。