地震作用下岸坡坝段侧向抗滑稳定对比分析

2019-01-16邵明磊杜慧超

西北水电 2018年6期

邵明磊，杜慧超

(中国电建集团西北勘测设计研究院有限公司，西安 710065)

0 前言

近年来中国水电事业高速发展，在大坝建设方面取得了显著的成效，在大坝建设中遇到的许多问题都得到合理的解决。就重力坝而言，岸坡坝段稳定对整个坝体的稳定影响较大，对于岸坡坝段稳定方面的问题研究的比较多，其中李永明[1]分别用刚体极限平衡法和有限元法2种方法，并且按分项系数法的原理对某重力坝岸坡坝段侧向稳定进行了分析研究；丁旭[2]等人对蟒河口水库岸坡坝段进行分区，并利用刚体极限平衡法，按可能失稳情况进行稳定应力计算,最后对结果进行了分析；宫照光[3]等人分别采用有限元和材料力学2种方法，对某重力坝岸坡坝段上游面裂缝对岸坡坝段稳定的影响进行了分析。地震因素是不可控制因素，对岸坡坝段的影响较大，容易造成岸坡坝段失稳。在地震作用下岸坡坝段动力稳定性的问题研究的比较少，王超[4]等人采用概率思想，并结合确定性矢量和安全系数方法，对设计基准期内随机地震条件下的重力坝岸坡坝段动力抗滑稳定性问题进行了初步探讨；邓良军[5]等人采用数值计算法和模型实验法对金安桥水电站岸坡坝段在地震作用下进行了动力分析。而对于地震作用下岸坡坝段侧向抗滑稳定问题的研究就更少了，为了对这一问题做进一步研究和分析，本文将结合某实际工程，选取其岸坡坝段，采用ANSYS有限元法，建立岸坡坝段三维有限元模型，在地震作用下进行应力计算，根据地基面上的作用效应和抗力计算结果，分析岸坡坝段在地震作用下的侧向抗滑稳定性。

1 计算方法和模型

1.1 抗滑稳定计算方法

根据SL 319-2005《混凝土重力坝设计规范》中规定，坝体抗滑稳定计算主要核算坝基面滑动条件，采用抗剪断强度公式计算坝基面的抗滑稳定安全系数[6]。

(1)

式中:K′为按抗剪断公式计算的抗滑稳定安全系数；f′为坝体混凝土与坝基接触面的抗剪断摩擦系数；∑W为作用于坝体上全部荷载(包括扬压力)对滑动平面的法向分值，kN；c′为坝体混凝土与坝基接触面的抗剪断凝聚力，kPa；A为坝基接触面截面积，m2；∑P为作用于坝体上全部荷载对滑动平面的切向分值，kN。

1.2 地震分析方法

1.2.1 拟静力法

根据SL 203-97《水工建筑物抗震设计规范》中规定，采用拟静力法计算重力坝地震作用效应时，只需考虑水平地震惯性力,计算公式为：

Fi=αhξGEiαi/g

(2)

式中：Fi为作用在质点i的水平向地震惯性力代表值；αh为水平向设计地震加速度代表值；ξ为地震作用的效应折减系数，取ξ=0.25；GEi为集中在质点i的重力作用标准值；αi为质点i的动态分布系数；g为重力加速度[6-7]。

动态分布系数应按照下式进行计算：

(3)

式中：n为坝体计算质点总数；H为坝高，溢流坝的H应算至闸墩顶；hi、hj分别为质点i、j的高度；GE为产生地震惯性力的建筑物总重力作用的标准值。

采用拟静力法计算重力坝地震作用效应时，水深h处的地震动水压力代表值应按下式进行计算：

pw(h)=αhξψ(h)ρwH0

(4)

式中：pw(h)为作用在直立迎水坝面水深h处的地震动水压力代表值；ψ(h)为水深h处的地震动水压力分布系数；ρw为水体质量密度标准值；H0为水深。

1.2.2 反应谱法

地震反应谱多指单自由度体系在给定的地震作用下最大加速度反应与体系自振周期的关系曲线。反应谱法的实质则为将计算结构的动力问题转化为静力问题进行求解，在计算地震响应时，将地面运动特征同结构动力特性一同纳入考虑的抗震计算方法[8-9]。

单自由度体系动力方程为：

(5)

式中：m为质量；x为位移；k为体系刚度；xg为地面运动水平位移；c=2mωζ，ζ为阻尼比，ω=(k/m)1/2。将各变量代入式(5)可得：

(6)

利用Puhamel积分可得：

(7)

加速度反应谱可定义为：

(8)

综上所述，通过反应谱法对结构进行动力响应分析，即将各震型作用效应采用平方和开放的组合法求解。

1.3 计算模型

利用有限元ANSYS软件建立岸坡坝段三维有限元模型。水流方向为X轴方向，向下游为正，铅直方向为Y轴方向，竖直向上为正，垂直水流方向(坝轴线方向)为Z轴方向，向右岸为正，坐标原点在该坝段计算模型坝踵高程最低点处。计算基础深度取2倍坝高，上游自坝踵位置处向上游取2倍坝高，下游自坝趾位置处向下游取2倍坝高，左右岸方向上自坝肩或坝体横缝处分别向左右岸延伸2倍坝高。计算域内单元划分基本采用八节点六面体实体单元，部分通过四面体实体单元进行过渡，坝体和地基均采用单元SOLID45进行模拟，地基与坝体相接部位设有5 m和3 m的过渡区域。坝体和5 m过渡区域采用八节点六面体实体单元，3 m过渡区域采用四面体实体单元进行过渡。坝体和5 m过渡区网格尺寸控制在1.0 m以内，3 m过渡区域以外地基单元边长为5～10 m，如图1、2所示。

图1 坝体有限元模型图

图2 地基有限元模型图

2 计算分析

2.1 拟静力法计算成果

2.1.1 岸坡坝段基底应力计算成果

该坝段在计算工况(正常运行+地震)情况下用材料力学法的拟静力法计算时，其基底X向最大拉应力出现在坝体上游边缘及坝肩右侧边缘处，为0.6 MPa；Y向最大拉应力出现在右侧坝肩处，为0.2 MPa；Z向最大拉应力出现在右侧坝肩上游边缘处，为1.0 MPa；切向最大剪应力出现在坝体上游边缘处，为0.6 MPa。基底最大拉应力值、最大压应力值及其出现部位见表1。

2.1.2 岸坡坝段侧向抗滑稳定计算成果

在计算岸坡坝段的侧向抗滑稳定中，将该坝段的坝基面整体进行分块计算，该坝段的抗滑稳定计算结果见表2。

表1 岸坡坝段基底最大应力表(拟静力法)

2.2 反应谱法计算成果

2.2.1 岸坡坝段基底应力计算成果

该坝段在计算工况(正常运行+地震)情况下用反应谱法计算时，其基底X向最大拉应力出现在坝体上游边缘及坝肩右侧边缘处，为0.4 MPa；Y向最大拉应力出现在右侧坝肩处，为0.3 MPa；Z向最大拉应力出现在右侧坝肩上游边缘处，为1.5 MPa；切向最大剪应力出现在坝体上游边缘处，为0.6 MPa。最大拉应力值、最大压应力值及其出现部位见表3。

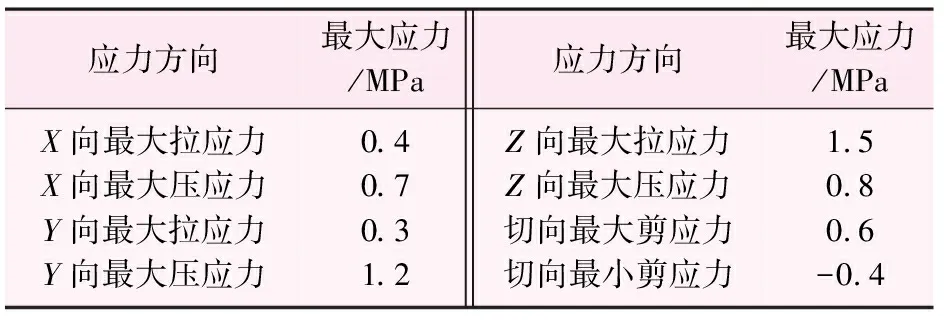
表3 岸坡坝段基底最大应力表(反应谱法)

2.2.2 岸坡坝段侧向抗滑稳定计算成果

在计算岸坡坝段的侧向抗滑稳定中，将该坝段的坝基面整体进行分块计算，该坝段的抗滑稳定计算结果见表4。

通过表1和表3对比分析可知，二者计算所得基底应力X向最大拉应力差幅0.2 MPa基本接近，均出现在坝体上游边缘及坝肩右侧边缘；Y向最大拉应力基本一致，均出现在右侧坝肩处；但Z向最大拉应力，拟静力法计算结果为1.0 MPa，反应谱法计算结果为1.5 MPa，二者计算结果差幅0.5 MPa偏大，均出现在右侧坝肩上游边缘处；切向最大剪应力差幅0.2 MPa基本接近，均出现在坝体上游边缘处。2种方法计算所得应力虽有些偏差，但出现的部位一致，且均小于Ⅲ类地基岩体允许承载力4.0 MPa，满足应力控制要求。

对比分析表2和表4可知，根据抗剪断试验资料，其中抗剪断摩擦系数f′取1.0，抗剪断凝聚力c′取800 kPa，在同样的分块情况及荷载组合下，侧向抗滑稳定计算结果二者均大于2.3，满足抗滑稳定要求，二者切向力计算结果基本一致，但反应谱法计算所得法向力结果较拟静力法偏大，从而反应谱法计算得到的抗滑稳定系数偏大。