制造业全要素生产率测算及影响因素研究
2019-01-16郭春娜
郭春娜
(1.河南科技大学 数学与统计学院,河南 洛阳 471000;2.中国社会科学院 研究生院,北京 102488)
一、引言及文献综述
2015年,中国开始供给侧结构性改革,其核心是提高创新能力与效率,习近平总书记强调“供给侧结构性改革的根本目的是提高社会生产力水平”,“供给侧结构性改革的主攻方向是……提高全要素生产率”,只有提高全要素生产率,才能促进经济的可持续发展与良性循环。中国成为世界强国的重要前提是要成为世界制造业强国,只有制造业才能让中国跻身于世界之颠,因此,2015年5月,国务院正式发布了《中国制造2025》,实施制造强国战略。由于技术引进已经进入了瓶颈,国外核心技术已难以引进,因此中国能否迈入世界制造强国要看中国制造业企业能否靠自身能力提高创新力和全要素生产率。但是,中国制造业劳动生产率与世界制造强国有较大差距,2010年中国制造业劳动生产率仅是德国的34%,日本的25%[1],提高全要素生产率才是提高劳动生产率的根本途径。所以制造业全要素生产率的提高不仅仅关系到《中国制造2025》的战略规划能否实现,中国能否进入世界制造强国行列,关系到中国能否真正实现供给侧改革,也关系到中国能否真正转变经济发展方式,跨越“中等收入陷阱”,实现经济的可持续发展。
全要素生产率(以下称为TFP)是指要素投入以外的原因导致的产出的增加。对TFP的研究主要有两大类方法:一是1957年索洛在新古典增长理论中提出的索洛余值法,索洛余值是总产出增长不能被投入要素增长所解释的部分,主要包括技术进步、资源配置效率、要素质量、公司治理策略、管理水平和分工的专业化等。利用索罗余值进行测算时,用得比较多的生产函数是1928年美国数学家Cobb和经济学家Douglas共同提出的Cobb-Douglas生产函数,除此之外还有1961年Arrow、Chenery、Mihas、Solow共同提出的CES生产函数,1967年Sato提出的多要素二级CES函数生产函数,1971年Revankar提出的VES生产函数,1973年L.Christensen、D.Jorgenson、Lau提出的超越对数生产函数[2]224-229。二是潜在产出法,就是通过估计前沿生产函数,然后通过计算实际的投入产出组合离前沿生产函数的距离的变化来测算TFP的变化。前沿生产函数的估计有两种方法:一种是参数方法如随机前沿分析法(SFA),一种是非参数法如数据包络分析法(DEA)。1953年瑞典经济学家Sten提出Malmquist指数的概念,1982年Caves等人通过距离函数构造了Malmquist生产率指数(即此后统称的Malmquist指数),但没有找到合适的度量方法,直到1978年Charnes、Cooper和Rhodes提出用DEA度量距离函数,Malmquist指数才得到了广泛的应用和发展。李春顶[3]、陶长琪和齐亚伟[4]等用该指数测算了中国的全要生产率。SFA方法是构造随机生产前沿函数,并把随机误差项分为单边误差项(表示距离函数)和对称误差项(表示随机环境因素对产出的影响),再结合Malmquist指数就可以测算出TFP增长率。
如何计算整体的TFP,文献上有三种方法,一种是由每个单元的TFP加权得到整体的TFP,这些单元可以是微观企业,也可以是空间区域或行业,如Brand等[5]、Bailey等[6]、Griliches 和Regev[7]、Foster等[8]、Olley和Pakes[9]、杨汝岱[10]、王志刚等[11]、姚战琪[12]等在研究中都用了这种方法,权重可以是市场份额、产出份额、从业人员数所占比重、资本所占比重等。另外一种方法是假设整体的产出是每个单元产出的CES函数,每个单元的生产函数仍满足C-D函数,从而计算出整体的TFP,如Hsieh和Klenow[13]。还有一种方法是将索洛增长模型及增长核算框架拓展到宏观层面,如蔡跃洲和付一夫[14]。
在对TFP的分解上,可以分解为体现型技术进步和非体现型技术进步,如郭春娜和秦青[15],也可以分解为技术进步与资源配置,如杨汝岱[10]、蔡跃洲和付一夫[14],还可以分解为技术进步、技术效率和规模报酬,如章祥荪和贵斌威[16]等。
TFP的研究是目前的一个热门问题,由于采用的数据、方法不同,或者对样本的处理不同,对中国TFP的估计结果有较大的差别。Young[17]认为,中国经济增长是依靠要素积累而非技术水平的提高。与之不同的是,Brand等[5]的研究发现1998—2007年中国TFP的年均增长率高达7.96%,且随着时间的增长速度加快,2002—2007年平均增长11%~16%。章祥荪和贵斌威[16]利用Malmquist指数法,测算出中国1979—2005年TFP年均增长率是1.6%。陶长琪和齐亚伟[4]利用Malmquist指数法,测算出中国1987—2007年28个省区TFP的增长多在1%以下。杨汝岱[10]利用中国工业企业数据库数据,通过OP方法和LP方法估计出1998—2007年制造业TFP增长率在2%~6%之间,年均增长3.83%。鲁晓东和连玉君[18]用参数和半参数等不同的方法计算出1999—2007年中国TFP年均增长率在2%~6.56%之间,而多数人的计算结果在3%~5%之间。
要想保持TFP的不断提升,就要深入研究TFP增长的主要动力——是企业成长带来的技术进步(技术效应)还是资源配置结构变化带来的效率的变化(结构效应)。近年来,从技术效应还是结构效应的视角对TFP进行研究是一个热点问题。Hsieh和Klenow[13]在规模报酬不变的假设下提出了利用TFP价值(TFPR)的离散程度来衡量资源配置效率。该方法被广泛使用,邵宜航等[19]用此方法测算了中国工业资源配置的扭曲程度。但Hsieh和Klenow的方法存在一定的不足,该方法假设企业的规模报酬不变,而一旦该假设不成立,TFPR的离散程度并不能准确衡量资源配置的效率,而且即使规模报酬不变的假设成立,他们提出的度量资源配置效率的方法只能衡量总体的资源配置效率,不能衡量单个要素的配置效率。龚关和胡关亮[20]对Hsieh和Klenow的模型进行了扩展,取消规模报酬不变的假设,并提出利用资本的边际产出价值(MRPK)的离散程度和劳动的边际产出价值(MRPL)的离散程度分别度量资本配置效率和劳动配置效率。原因是由于生产要素的边际报酬递减,如果要素的边际产出价值趋于离散,说明要素从边际产出高的行业或地区流向了边际产出低的行业或地区,从而导致要素配置效率降低。但无论是Hsieh和Klenow还是龚关和胡关亮,他们都认为资本产出弹性和劳动产出弹性仅仅依赖于行业,也即只要是同一个行业,其资本和劳动的产出弹性都相同。然而,不同所有制性质的企业生产规模往往不同,比如国有企业通常有比私营企业更大的规模,不同的生产规模决定了不同的规模报酬状况,从而也意味着要素的投入产出弹性不同。对企业规模与规模报酬的关系,平狄克和鲁宾菲尔德[21]194-197、高鸿业[22]143-145在西方经济学理论中早有阐述:在企业生产扩展的开始阶段,厂商由于扩大生产规模而使经济效益得到提高,这便是规模经济。当生产扩展到一定的规模以后,厂商继续扩大生产规模,就会使经济效益下降,这便是规模不经济。此外,不同所有制性质的企业配置资源的方式也不同,国有企业更多地靠行政手段,私营企业更多地靠市场调节。因此,即使是同一个行业,如果属于不同的所有制,就会有不同的生产规模和不同的资源配置方式,从而导致有不同的规模报酬状况和不同的要素投入产出弹性。
本文对龚关和胡关亮的模型进行了改进,突破了投入要素的产出弹性只与行业有关的假设,认为资本产出弹性和劳动产出弹性不仅依赖于行业,也依赖于企业的所有制性质,构建了一个新的异质产品的垄断竞争模型。然后,根据所构建的模型,结合中国工业企业数据库中企业层面的微观面板数据,运用OP方法测算了中国制造业的TFP、资本配置效率和劳动配置效率,并分析了TFP的地区差异。最后,根据Olley和Pakes[9]的方法测算了技术进步水平,并从技术进步和资源配置的视角分析了中国制造业TFP的影响因素。
二、模型设定、数据来源与样本处理
(一)模型设定
本文设定的异质产品的垄断竞争模型如下。
假设消费者消费的最终商品是Y,该商品由一个代表性厂商在完全竞争市场上生产。社会中存在S个不同的行业,这些行业的产出是这个代表性厂商的投入要素,行业i的产出是Yi,假设代表性厂商的生产函数是C-D生产函数:
(1)
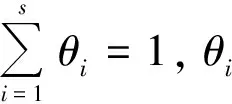
PiYi=θiPY
(2)
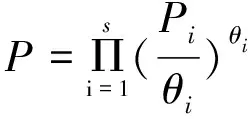
每个行业都存在生产异质性产品的厂商m,其产出为Yim,行业i的总产出与各个厂商产出的关系满足CES生产函数:
(3)
其中Mi表示行业i内厂商的数量,可以得到行业i厂商m的产品Yim的反需求函数是:
(4)
假设行业i厂商m生产函数是:
(5)
其中j表示所有制。
此处与龚关和胡关亮不同在于资本产出弹性αij和劳动产出弹性βij不仅依赖于行业i,也依赖于所有制j。
假设劳动扭曲和资本扭曲分别是τL,im和τK,im,则企业利润最大化问题可以表示为:
max{Pim(Yim)Yim-(1+τL,im)ωLim-(1+τK,im)RKim}
(6)
根据利润最大化条件可以得到厂商的定价公式:
(7)

从而得到行业i厂商m劳动的边际产出价值是:
(8)
行业i厂商m资本的边际产出价值是:
(9)
至此,本文的推导步骤与龚关和胡关亮一致,不同的地方在于对行业i厂商m的生产函数参数设定的不同以及由此带来的MRPK和MRPL的公式的变化。
则MRPK和MRPL的离散程度可以表示资本和劳动的配置效率。
根据公式(5)可知,行业属于i、所有制性质属于j的样本m的TFP的计算公式是式(10),TFP增长率的计算公式是式(11)。
TFPm=exp[ln(Ym)-αijln(Km)-βijln(Lm)]
(10)
(11)
按照Olley和Pakes[9]的方法,各个单元TFP的简单平均(不加权)代表企业的技术水平也就是技术进步,因此,技术进步公式如下:
φ=TFPm
(12)
(二)数据来源、研究步骤与样本处理
本文数据来源于《中国工业企业数据库》的制造业样本企业,用样本企业的成品产量作为产出变量,用资本总额和从业人员数分别作为资本投入变量和劳动投入变量,且根据2012年的《中国城市(镇)生活与价格年鉴》的工业生产者出厂价格指数和固定资产投资价格指数分别对产出变量和资本投入变量进行平减。
研究步骤及样本处理过程是:(1)剔除指标不全的样本,并按“行业×所有制”建立210个半参数OP模型,分别估这些模型的参数和TFP。(2)处理极端异常样本和离群样本,本文认为如果某个样本的TFP增长率小于-100%或大于100%,即把该样本作为极端异常剔除,然后再根据箱形图原理剔除TFP增长率离群的样本。(3)为了保证测算结果的准确性,对于剔除极端异常样本和离群样本后余下的样本再次建立模型并估计产出弹性和TFP,然后根据公式(8)和公式(9)计算出各样本的劳动的边际产出价值、资本的边际产出价值,并计算其标准差(见表1),标准差即可表示资本和劳动的配置效率。再根据公式(10)和公式(11)计算出每年各样本的TFP及增长率,根据公式(12)计算出每年的技术进步水平,本文按照杨汝岱[10]的加权方法得到制造业整体的TFP及增长率,权重分别用劳动投入、资本投入和成品产量,然后把三种计算结果取简单平均(见图1)[注]由于篇幅有限,本文省略中间测算结果,感兴趣的读者可以向作者索取。。
三、实证结果
(一)制造业整体TFP增长率
从整体看,中国制造业TFP增长率如图1所示,2001—2011年TFP增长率年均值是2.36%,但波动明显,随着时间的增长,有明显的降低趋势,2001—2007年TFP增长率年均值是4.93%,2008—2011年TFP增长率年均值是-2.14%。2003年、2009年、2010年都是负值且2010年最低,这意味着2003年的非典,特别是2008年的金融危机对制造业企业有着非常明显的影响,可能的原因:一是因为金融危机期间出口严重下滑,内需不足,企业相应减少产出,尽管一部分资本和劳动退出生产,但仍有部分资本和劳动并没有退出生产而是以非充分使用的方式继续投入生产,由此造成TFP增长率下降。二是因为为了应对金融危机,中国政府推出了刺激经济增长的十大措施,这些措施共投资约4万亿,大规模的投资刺激可能带来资源配置扭曲、价格机制失调,严重挤占了TFP的增长空间。如果扣除掉金融危机的影响(即不计算2009和2010年的值),样本期内TFP增长率年均值是5.64%,所以金融危机使得TFP增长率降低了3.28个百分点。如果同时扣除掉非典和金融危机的影响(即不计算2003、2009和2010年的值),则样本期内TFP增长率年均值是7.03%,所以非典和金融危机的共同作用使得TFP增长率降低了4.67个百分点。本文计算的制造业整体的TFP增长率与杨汝岱[10]的研究非常接近,他们的研究也发现TFP的增长在放缓,可能的原因是因为本文采用的数据来源与他们相同,都是中国工业企业数据库中企业层面的微观数据,都是对制造业TFP增长率的估计。
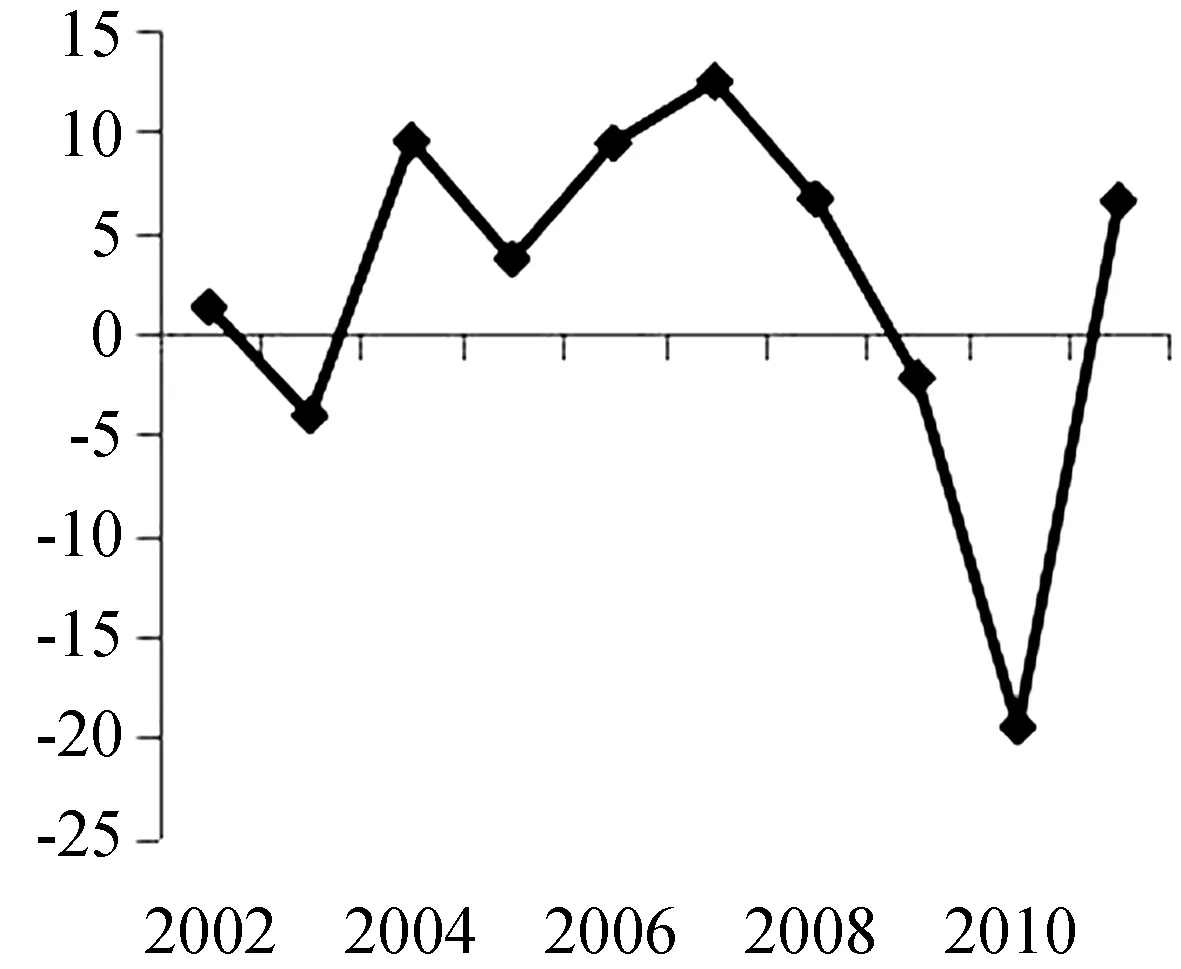
图1 中国制造业整体TFP增长率(单位:%)
(二)制造业TFP增长率的差异:跨地区比较
根据2001—2011年各省份TFP增长率的平均值对地区进行聚类,发现山西、青海、宁夏、云南等12个省份的TFP增长率较高,在2.76%~4.36%之间;福建、广东、西藏、海南等19个省份的TFP增长率较低,在1.08%~2.59%之间(不包括中国的台湾、香港和澳门)。
分析发现TFP增长率都与TFP有正向关系,TFP越高,TFP增长率也越高,比如山西、青海、宁夏和云南,他们不仅年均TFP及其增长率较高,而且在多数年份TFP增长率都处于领先地位。对TFP增长率与TFP的关系进行统计学检验,按照K均值聚类方法,把全国31个省份的TFP聚为两类,检验TFP较高的一组是否TFP增长率也较高,T检验的结果显示P值是0.007,从而可以认为TFP较高的省份的TFP增长率也显著高于TFP较低的省份,这意味着地区间制造业TFP的差异越来越大。
进一步对样本期内生产要素在地区间的变动进行分析(仅根据调整后余下的样本计算),先分析从业人员数的变动,从2001到2011年,TFP增长率较高的12个省份中,除3个省份(辽宁、内蒙古、宁夏)外都是劳动力净流出,甘肃劳动力净流出最多,年均净流出3.8万人,劳动力净流入最多的都是发达地区,前5名(从高到低)依次是广东、江苏、浙江、山东、福建,年均净流入分别是77.6万、42.9万、25.4万、24.9万、16.1万。再看资本存量在地区间的变动,从2001到2011年各地区资本存量的增加差别很大,年均增加最少的前10名(其中有8个都是TFP增长率较高的省份)依次是:西藏、海南、青海、宁夏、甘肃、贵州、新疆、云南、黑龙江、吉林,年均增加量分别是-1.54亿元、33.9亿元、34.9亿元、105亿元、133亿元、161亿元、175亿元、182亿元、226亿元、327亿元。年均资本存量增加最多的前10名依次是(按年均值从高到低)江苏、广东、浙江、山东、辽宁、河北、湖北、四川、河南、上海,年均增加量分别是4 420亿元、3 590亿元、3 070亿元、2 850亿元、1 310亿元、1 210亿元、1 060亿元、985亿元、959亿元、920亿元。
经过以上分析可以发现,东部发达地区具有相对越来越低的TFP,但同时又有着相对较高的资本流入和劳动流入,由此带来的一个思考是:正如前文所示,中国制造业整体TFP增长率下降,2001—2007年均增长率是4.93%,2008—2011年均增长率仅为-2.14%,那么TFP增长率的下降是否是由于资源配置的扭曲导致的?是否是由于资本和劳动从高增长地区流向了低增长地区导致的?还是由于企业技术进度速度的降低导致的?下文的实证结果给出了结论。
(三)技术进步与资源配置效率变化趋势
在度量资源配置效率时,本文采用MRPK与MRPL的离散程度度量资本配置效率与劳动配置效率,其中σ的取值按照Hsieh和Klenow、龚关和胡关亮的方法,取σ=3。图3和图4给出了MRPK与MRPL取对数后的核密度函数,从图中可以看到,随着时间的推移,MRPK均值逐渐降低,不仅MRPK较低的企业逐渐降低,MRPK较高的企业也逐渐降低,即密度曲线中心轴左移,同时左尾部变厚,右尾部变薄;MRPL均值逐渐提高,不仅MRPL较低的企业逐渐提高,MRPL较高的企业也逐渐提高,即密度曲线中心轴右移,同时左尾部变薄,右尾部变厚,但图中MRPK和MRPL的离散趋势不明显,也即资本配置效率与劳动配置效率的变化趋势不能直观看出。

图3 MRPK的核密度函数

图4 MRPL的核密度函数
根据公式(8)、公式(9)取对数后的标准差可以计算出资本配置与劳动配置的扭曲程度的变化,根据公式(12)计算出技术进步的变化,结果见表1。
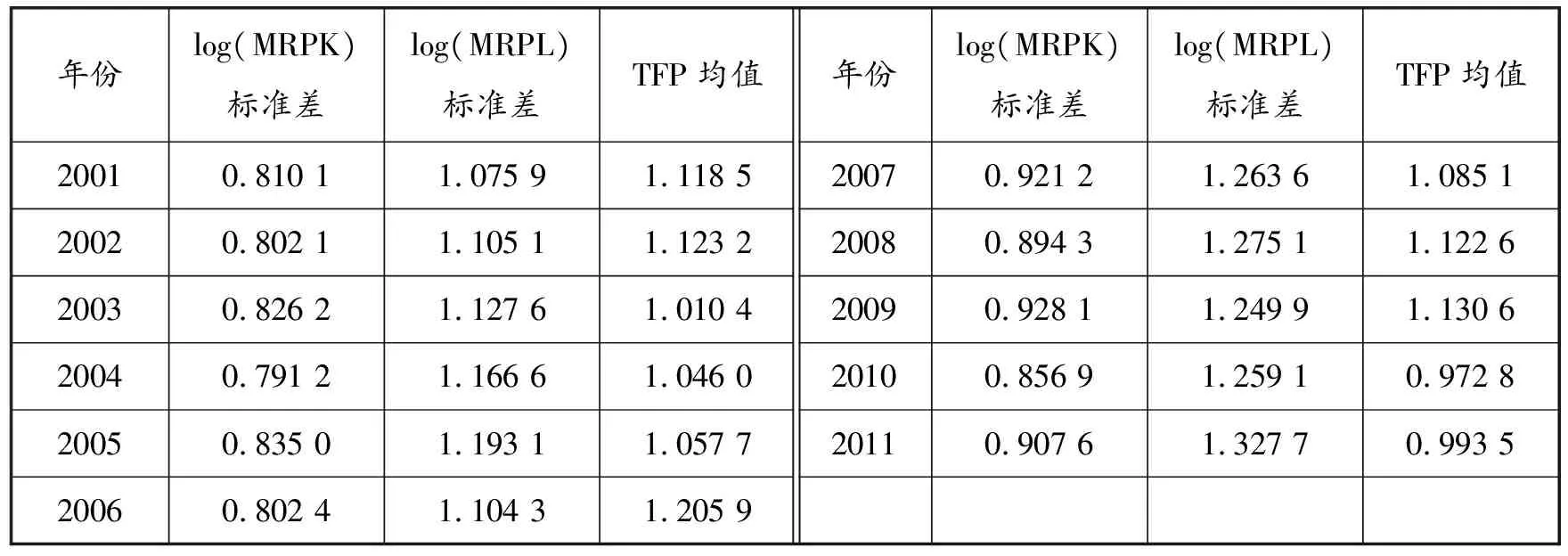
表1 资本配置与劳动配置的扭曲程度和技术进步(单位:%)
从表1中可以直观看出,2006年以后,资本配置扭曲、劳动配置扭曲都要高于2006年以前,因此按时间分为两段,一段是2001—2006年,另一段2007—2011年。T检验显示,2007—2011年资本配置扭曲、劳动配置扭曲都显著大于2001—2006年(P值都等于0)。进一步对不加权的TFP的平均值(即技术进步)进行T检验,结果显示两段时间技术进步的差异不显著(P值等于0.42)。回归分析显示,2001—2011年间,log(MRPK)标准差和log(MRPL)标准差年均增长分别为0.01%和0.02%且系数显著,而技术进步随时间的变化趋势不显著。同时,2001—2006年,log(MRPK)标准差、log(MRPL)标准差、技术进步随时间的变化趋势都不显著,因此可以得到如下结论:2006年以后TFP增长率的显著下降不是由于技术进步的下降导致的,而是由于资本配置效率与劳动配置效率的双重下降导致的。该结论与杨汝岱[10]相同,他的研究也发现制造业TFP的增长越来越依靠企业本身的成长,企业间配置效应的作用越来越小。而蔡跃洲和付一夫[14]、龚关和胡关亮[20]的研究则认为资源的配置效率是逐渐改善的。本文结论与之不同的原因一是模型设定的不同,本文认为资本产出弹性和劳动产出弹性不仅依赖于行业,也依赖于所有制,相比于资本产出弹性和劳动产出弹性仅仅依赖于行业的模型,本文的模型更符合现实,测算结果更准确;二是本文是对中国制造业TFP的研究,而不是中国整体的TFP,原因是本文的TFP是根据微观数据测算,尽管进行各种加权得到了制造业的TFP,但仍然不是宏观意义上的TFP。
正如前文所示,2001—2011年大量的资本和劳动流向了TFP较低的地区,造成资源配置效率下降,同时企业的技术进步没有显著提高,这是中国制造业TFP增长率放缓的主要原因,这也充分证明促进区域协调发展,鼓励沿海地区产业向欠发达地区转移的重要意义,不仅能加快欠发达地区的发展,缩小收入差距,也能从整体上提高资源配置效率,进而提高制造业的TFP。在中国经济增长的初期,通过劳动力从农业转向非农业,提高了资源配置效率,促进了经济的快速发展。本文的研究也意味着,在现阶段,中国经济的发展仍然具有后发优势,仍然可以通过体制改革、政府的宏观调控、政策制定等促进劳动力和资本从低效率向高效率部门和地区转移,进而提高资源配置效率。同时应该促进市场的公平竞争、充分发挥市场在资源配置中的决定性作用,这样能刺激商品生产者改进技术、提高劳动生产率,进而促进整个社会技术水平的不断提高,这样,在资源配置效率的提升和技术进步的共同作用下,未来中国制造业的TFP仍然会有较大的增长空间。
四、结论及政策建议
本文利用工业企业数据库中企业层面的微观面板数据,首先按“行业×所有制”建立210个OP模型,测算了资本产出弹性、劳动产出弹性、企业层面的TFP及增长率、劳动的边际产出价值、资本的边际产出价值,然后根据加权法计算出中国制造业各地区、制造业整体的TFP及增长率,最后根据Hsieh和Klenow以及Olley和Pakes的方法从技术进步和资源配置的视角分析了中国制造业TFP增长的深层次原因。研究结果如下:第一,中国制造业整体TFP增长率下降。中国制造业在2001—2011年的TFP增长率是2.36%,2006年以后明显下降,2007—2011年平均增长仅0.77%,制造业TFP增长率在2003年、2009年和2010年有着明显的下降,且在2010年达到最低。这意味着2003年的非典,特别是2008年的金融危机对制造业企业有着非常明显的影响,金融危机使得TFP增长率降低了3.28个百分点,非典和金融危机的共同作用使得TFP增长率降低了4.67个百分点。第二,2006年以后中国制造业TFP增长率下降的原因是资本配置效率与劳动配置效率的双重下降。发达地区如广东、福建、北京、上海等具有相对越来越低的TFP,但同时又有着相对较高的资本流入和劳动流入,因此随着时间的增长,资本配置效率和劳动配置效率都显著下降,但技术进步并没有显著提升,这是中国制造业整体TFP增长率下降的主要原因。
因此,本文根据理论模型和实证结果提出如下的政策建议。
其一,充分发挥市场在资源配置中的决定性作用。要靠市场的力量调节生产资料和劳动力在各生产部门、各地区的分配,市场对资源的配置主要是通过价格、竞争和供求等发挥作用来实现。价值规律告诉我们,竞争能刺激商品生产者改进技术、改善经营管理、提高劳动生产率,其结果必然是推动整个社会的技术进步,促进整个社会的生产力水平不断提高。正如本文的研究所示,当前中国经济结构不合理,经济发展方式转变迟缓,技术进步不显著,根本原因是存在着许多妨碍市场主体创新的体制障碍,在相当程度上,政府充当了资源配置的主角,导致资源配置效率下降,企业创新动力不足,如果能充分发挥市场在资源配置中的决定性作用,就能更好地发挥价值规律的作用,使商品生产者在竞争中优胜劣汰,进而提高全社会的生产力水平。
其二,鼓励制造业从东部发达地区向其他地区迁移。正如本文研究所表明的,东部发达地区TFP相对越来越低,但是资本流入和劳动力流入却远高于TFP相对越来越高的中西部地区,由此带来的资本配置效率和劳动配置效率的双重下降是导致制造业TFP增长率下降的主要原因。目前东部、中部、西部经济发展的差距很大,不仅是产出规模上的差距,还有生产率的差距,东部地区的高产出是依靠较高的资本投入和劳动投入得到的,因此,政府要做好宏观调控,制定相应的政策促进区域协调发展,鼓励沿海地区产业向欠发达地区转移,这样不仅能缩小收入差距,也能从整体上提高资源配置效率,进而提高制造业的TFP。
