一种基于SVM的线性分类算法

程凤伟

(太原学院,山西 太原 030032)

引言

为了使支持向量机理论应用于无监督学习,Tax 和 Duin[1]提出了单类支持向量机算法,成功地应用于层次聚类[2-3]和核聚类等算法中[4-5],单类SVM分类算法的主要思想是用一个适当的函数[6-7]代替内积将数据点映射到高维特征空间,在特征空间里找到一个能包含最多数据点映射的最小范围,单类SVM算法的关键步骤在于解决一个有关样本维度的二次规划问题。随着样本数目的增加,算法的复杂度也越来越高。为了避免解决二次规划问题,本文提出了基于SVM的单类线性分类算法(Linear One-Class Classification Algorithm based on SVM,LOSVM),采用两种方法分别消除二次项和不等式。首先,增强约束不等式方程;其次,为拉格朗日惩罚项加平方。计算出简化的拉格朗日公式后,便可得到一组计算简便的线性方程。本文提出的新的分类算法可以应用到聚类和核聚类问题中。实验结果表明,本算法与单类SVM算法相比,在正确率不变的情况下,运行速率大大提高。

1 基于SVM的单类线性SVM模型

单类SVM算法是一种针对只有正类样本组成的数据集进行处理的核方法,算法的主要思想是计算出在特征空间能包含所有样本映射的最小超球。

‖φ(xi)-α‖2≤R2ξ+εi

(1)

其中,‖·‖是欧几里得范数,a是超球的中心,R是超球的半径,ξi是松弛变量,ξi≥0,i=0,1,2…n,为了解决这个问题,我们引入

(2)

其中,αi≥0和βi≥0,i=1,2,3…n,αi,βi是与公式(1)及ξi相关的拉格朗日乘子,C用来权衡算法的简易性和容错程度。

根据以上算法模型,本文提出了基于SVM的单类线性SVM算法(LOSVM),通过以下两种方法来实现本文的算法:

1)将上述公式(1)中不等式增强为等式,转化为:

‖φ(xi)-α‖2=R2+ξi

(3)

2)将拉格朗日转化为:

(4)

接着,我们将本文提出的LOSVM算法应用于层次聚类和核聚类。

将LOSVM算法应用于层次聚类算法。在高维特征空间得到的超球模型由若干部分组成,每部分是一个包含数据点的独立聚类,定义R(x)为特征空间数据点到超球中心的距离函数,R作为最小超球的半径,那么数据空间中球面的投影集合是{x|R(x)=R}。图1是单类SVM算法和LOSVM算法在同一数据集上的聚类结果的示意图,数据集由220个点组成,其中右上60个点,左下60个点,中间100个点。从图1可知,LOSVM算法的误差大于单类SVM算法的误差,因为在边缘的数据点(ξi>0)会被较小的球拒绝,然而对于LOSVM来说,为每一个数据点分配一个聚类并不是必要的。我们采用层次聚类算法对内部的点(ξi<=0)进行标记,对于外部的数据点(ξi>0)采用K近邻算法[8]进行标记。显然,LOSVM算法可以将数据集划分为两部分:内集和边缘集,而边缘集包含了潜在支持向量,这些支持向量可以在单类SVM算法模型中进一步训练。因此,LOSVM可以用于支持向量机的预处理,它也适用于在一定条件下的监督学习,基于LOSVM的预处理算法也正在进一步研究中。

将LOSVM算法应用于核聚类。核聚类算法侧重于数据点与中心点的距离,而不是数据集投影的精确形状,LOSVM算法获得的超球虽然比较小,但是超球中心点的功能并不低于用K近邻算法求得的中心点的功能。

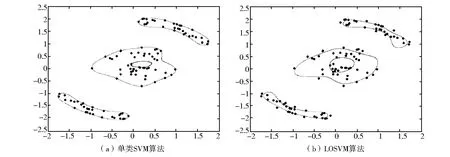
图1 单类SVM算法与LOSVM算法的聚类结果示意图

2 实验结果

将本文提出的算法与基于单类SVM核聚类算法和经典K-均值聚类算法进行比较,实验采用著名的IRIS数据集,LOSVM算法中惩罚参数C取值为1000,q取值为0.78;单类SVM算法中C取值为1.0,q为0.78.

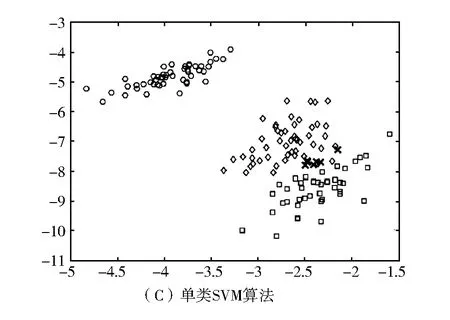
图2 三种方法的聚类结果

图2给出了三种方法的聚类结果,图中用粗体十字来表示被错误聚类的数据点。实验得出,K-均值聚类算法的正确率是88.7%,LOSVM算法的正确率是94.7%,单类SVM算法的正确率是96%,LOSVM算法与其他两个算法相比,运行速度有很大的提高,运算精度虽有所下降,但在可接受范围内。

3 结束语

本文提出了一种基于单类SVM的新型分类器LOSVM算法,通过消除方程中的二次方项大大提高了算法的运行速度,并将该算法应用于层次聚类和核聚类。在实验中,虽然LOSVM的误差大于单类SVM算法,但是LOSVM算法的运行速度较单类SVM算法有很大提高,同时说明LOSVM适合用于单类SVM算法的预处理算法,当将LOSVM应用于核聚类算法时,LOSVM的准确率几乎与单类SVM相同。在未来的工作中,考虑将LOSVM算法应用于对称矩阵和其他一些复杂算法的预处理算法中。