基于多智能体协商的公交分布式滞站控制策略

王志利，张昕明

(1.山西省城乡规划设计研究院工程设计中心，太原 030001；2.青岛海信网络科技股份有限公司，山东 青岛 266000)

优先发展公共交通，并不是只扩充公交车辆数，单方面增加供给，而应该根据公交需求，合理利用现有公交资源，实现公交均衡运量，提高公交运行准点率和满载率。现实公交车辆运行过程中，往往会出现“公交串车”的现象。这种现象主要由两个原因引起：一是车辆在公交站点间行程时间的不稳定性；二是乘客需求的时变性。这些因素导致了公交车辆到站间时间间隔的不稳定，从而增加了乘客的平均等待时间。尤其是在公交需求量大、公交车辆经常超载的情况下，这种影响会更加明显。

为避免公交串车现象，需要对公交车辆进行行车控制，常用的策略就是滞站策略[1]，可以分为两类，一类是通过车辆滞站来匹配既定的运行时刻表，另一类是通过滞站均衡车辆到站时间间隔。Daganzo以尽可能保持公交车辆最快运营速度为出发点，提出了使车辆到站时间间隔近似均匀的自适应控制策略[2]。控制策略基于前车的实时信息动态的决定车辆在滞站点的滞站时间。但其在交通干扰较大时，控制策略的效果并不能令人满意。为了克服这个问题，Daganzo和Pilachowski又基于公交前后辆车的间距，提出了一种双向合作的协同策略[3]。Bartholdi和Eisenstein则不以到站时间间隔均匀为目标，而是寻找能够适应当前系统的最优的到站时间间隔[4]。滕靖、杨晓光以优化全线车辆加权离站车头时距方差为目标，建立了基于APTS 条件下公交车辆单线路实时控制模型[5-6]。李细霞考虑了中途站点的车辆停靠行为对乘客候车时间的影响，建立了一种车辆停靠控制模型，达到了均衡中途各站待运乘客的候车时间的目的[7]。董高成等针对快速公交系统车辆出现串车和大间隔对车辆延误和乘客候车满意度的影响较大的情况，提出了一种基于区段划分的实时行车控制算法，为了进一步降低间隔不合理的情况，提出了对多线BRT汇入点的控制方法[8-9]。

本文构建了公交车分布式滞站控制的多智能体结构体系，结合边际费用计算方法，基于多智能体协商机制，设计了基于智能体协商机制，分布式的公交行车滞站控制策略。

1 问题描述

1.1 公交网络

本文以单向环路公交线路为例研究，如图1所示，公交线路包含K个站点和N辆公交车。

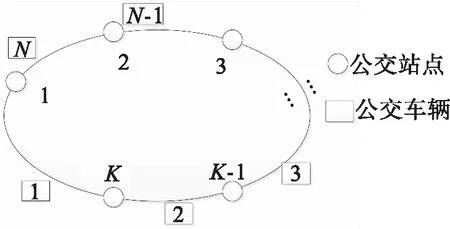
图1 公交网络
Fig.1 Public transport network

1.2 符号定义

ai,k——车辆i到达站点k的时间；

di,k——车辆i在站点k的离站时间；

λk(t)——t时刻站点k处乘客到达率；

Bi,k——车辆i在站点k上车乘客数量；

Gi,k——车辆i在站点k下车乘客数量；

tm,k——乘客m到达站点k的时刻，m∈Pk(t1,t2)；

bm,k——乘客m在站点k处的上车的时刻，m∈Pk(t1,t2)；

Mk(t1,t2)——在(t1,t2)时段内已经到达站点k的乘客的数量；

Pk(t1,t2)——在(t1,t2)时段内已经到达站点k的乘客的集合。

1.3 目标函数

在公交出行中，由于天气等因素，乘客在车外等待较车内等待更为不便，所以将乘客的等待费用分为车外的等待费用和车内的等待费用。

(1)车外等待费用WF，即乘客在车站等待公交车辆到来的费用，可由下式计算得到：

其中fF(t)为单个乘客车外等待的费用函数，fF(0)=0，当t≥0时，fF(t)≥0，t为乘客的等待时间。

(2)车内等待费用WN，即乘客在车内等待车辆出发时的费用，可由下式计算得到：

WNi,k=(Bi,k-1-Gi,k)·fN(di,k-ai,k)+

其中fN(t)为单个乘客车内等待的费用函数，fN(0)=0，当t≥0时，fN(t)≥0.

费用函数fF(t)和fN(t)的形式如下：

fF(t)=K1FtK2FeK3Ft,fN(t)=K1NtK2NeK3Nt，如果令K1F=K1N=K2F=K2N=1，K3F=K3N=0，则fF(t)=t,fN(t)=t.

模型的目标是使乘客的平均等待费用最小化，包括车外等待费用和车内等待费用，目标函数如下式：

其中NP为所有乘客的总数。

2 实时分布控制方法

2.1 结构框架

本文设计了分布控制的多智能体结构框架，如图2所示，Stop Agent表征该站点的控制策略，并且储存相邻站点的信息。Bus Agent利用这些信息在不同的Stop Agent中进行协调，以达到最优方案。

图2 多智能体系统结构图
Fig.2 Multi-agent system structure

2.2 协商机制

本文设计了基于边际费用计算的协商算法。滞站策略的实施会增加车内的等待费用，但由于时间间隔(di,k,di+1,k)的长度会逐渐的减小，相应的车外的等待费用也会降低。因此，当车内等待的边际费用与预期的车外等待的边际费用相等时，就会形成局部的最优化。

假设在t时刻，对车辆i和站点k协商。车内等待的边际费用MNi,k(t)如下：

预期的车外等待的边际费用MFi+1,k(t)则较为复杂。车外等待费用的期望E(WFi+1,k|t)如下所示，

其中，fai+1,k(y)是下一辆车到达时间的条件概率密度函数。则预期的车外等待的边际费用为：

给定费用函数为fF(t)=fN(t)=t，则

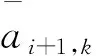
2.3 最优化条件

上述协商机制只是最优化的必要条件，需要进行适当约束，使其成为最优化的充分条件，再此引入两个引理，引理证明过程详见文献[9]：

引理1：若fN(t)为凸函数，则车内等待边际费用函数MNi,k(t)对于t单调递增。

由于滞站策略在减少车外等待时间的同时相应增加了车内的等待时间，故可以将车内等待时间的增加看作成本，车外等待时间的减少看作价格，则控制目标即为使利润最大化。由引理1和引理2可知，当成本曲线和价格曲线斜率相等时，即为最优化，如图3所示。

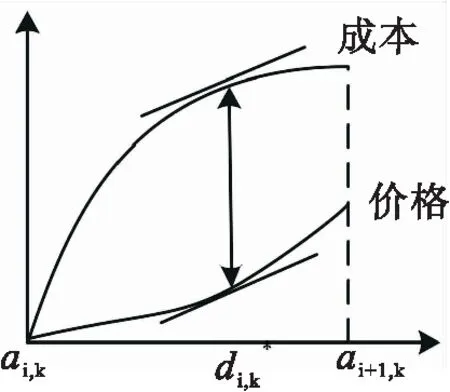
图3 最优化条件
Fig.3 Optimal conditions

即最优化的滞站时间满足：

MNi,k(di,k*)=MFi+1,k(di,k*)

由此得到协商算法：

Step1：在t0时刻，Bus Agent和Stop Agent分别计算他们的边际费用MNi,k(t)和MFi+1,k(t)；

Step2：若MNi,k(t)≥MFi+1,k(t)，则不滞站；否则，滞站并更新时间，令t0=t0+Δt，回到Step 1.

3 仿真实验

3.1 基本设置

设置包括10个站点、5辆车的公交线路，每个站点的乘客的到达率符合泊松分布，且到达率λ=1.0/min.每个站点乘客的下车率ρ=0.4，两个站点之间的行程时间服从对数正态分布，期望TBS=5min，方差σ2=4，费用函数fF(t)=fN(t)=t.每个乘客的上车所用时间DW=0.05min.

3.2 策略设置

设置四种策略进行比较分析：

(1)无策略(No Wait)：对车辆不进行控制，没有上车或下车人数时车辆即开出。

(2)基于车-车间隔的滞站策略(Headway-Based)：车辆在进站后进行滞站，目的是使该车辆与前、后同线路车辆时间间隔均匀。

(3)基于时刻表的滞站策略(Schedule-Based)：当车辆到站时间早于时刻表既定时间，则滞站以符合时刻表运行。

(4)基于边际费用的协商滞站策略(Negotiate)：利用本文提出的算法进行滞站。

通常在制定公交时刻表的过程中，都会在到站时间上留有余地，即若两站点间的行程时间为TBS，余留时间。

3.3 仿真结果

(1)情景1：公交车辆运行过程中未发生异常扰动，即交通状况、站点需求都在预期内，公交车辆能够按照既定时刻表按时发车，公交正常运行。

假设所有车辆在始发站处都按时出发，则在实施不同的控制策略的基础上，相比于不实施策略(No Wait)而言，在不同的既定间隔的情况下，乘客等待时间的减少率如图4所示。

图4 不同既定间隔下的等待时间变化趋势
Fig.4 The relationship of the waiting time versus different intervals

可知当既定间隔较小时(小于15 min)，Negotiate策略效果较好；当既定间隔在15～20 min之间时，三种策略的性能相当；而当既定间隔较大时(大于20 min时)，Schedule-Based策略的效果更为明显。

(2)情景2：公交车辆在行驶过程中遇到计划外的突发干扰，如站点需求激增、路段严重拥堵、道路交通事故等，导致车辆运行延误较大，不能按既定时刻表发车。

由于车辆在行驶中的延误，可能会导致始发站发车班次的延迟，设定既定间隔SH与其他参数之间的关系为：

SH=TBS(1+s)·NS/NB

其中NS为站点数，NB为车辆数。

不同的策略下既定间隔与乘客平均等待时间关系如图5所示。

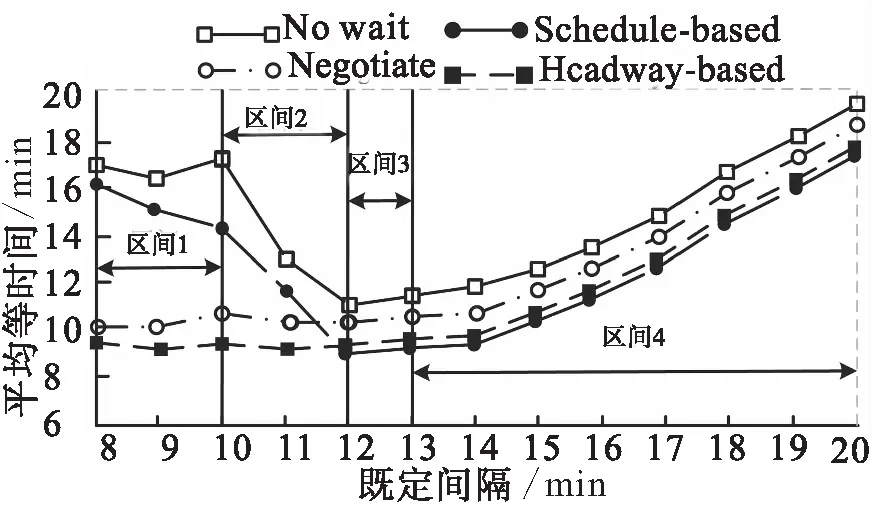
图5 不同的策略下既定间隔与乘客平均等待时间关系
Fig.5 The relationship between the given intervals and average passenger waiting time with different strategies

由图5可知，既定间隔在区间1和区间2时，No Wait和Schedule-based策略的平均等待时间随滞站时间增大而减少，但变化趋势不稳定，而Negotiate和Headway-based策略则表现稳定且平均等待时间均较小，这是因为Negotiate和Headway-based两种策略并不依赖于固定的时刻表，具有自组织的能力；区间3内四种策略都较稳定，区间3为最佳的既定间隔；区间4内随既定间隔的增大，平均等待时间递增，可见既定间隔不宜超过区间3的范围。由图可知车辆的最佳时间间隔为12 min，由

SH=TBS(1+s)·NS/NB

得到滞站时间s为0.2.

为更深入对四种策略进行比较分析，研究四种策略下各站点到站时间间隔的变异系数及平均到站时间间隔。由图6所示，Headway-based策略各站点到站时间间隔的变异系数最小，No Wait策略的变异系数最大，说明在不实施任何策略情况下车辆的到站间隔极不均匀；而由图7所示，Headway-based策略虽然变异系数小，但是其平均到站时间间隔为13.5 min，为四种策略最大。综合图6和图7，Negotiate策略均表现稳定，具有很好的鲁棒性。

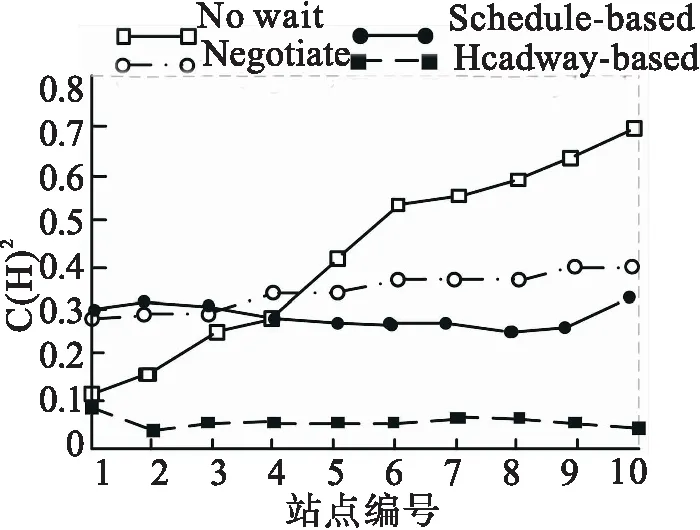
图6 各站点到站时间间隔变异系数
Fig.6 Each site arrival time interval of coefficient of variation

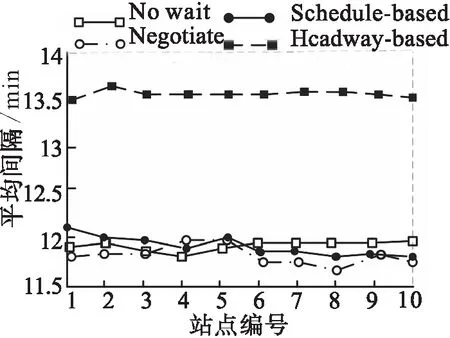
图7 各站点平均到站时间间隔
Fig.7 The average arrival time interval of each site

4 结 论

由于公交车辆在运行过程中经常受到外界干扰导致公交服务质量降低，乘客等待时间增加。本文根据车内、车外乘客的边际等待费用，设计了Bus Agent和Stop Agent之间的协商算法，提出了公交车辆的分布式滞站控制策略，能够通过对车辆的发车滞站控制，降低外界路况、需求等异常情况对公交运行的影响，提高公交服务的可靠性。仿真实验表明本文提出的算法对于不同的车辆运行情景具有很好的鲁棒性，能够显著降低乘客平均等待时间，提高公交服务质量。不过，由于乘客需求的时变特性难以准确把握，目前在公交运行中车辆的运力安排并不能与需求相匹配，存在运力不足或浪费的现象。今后的研究将重点解决乘客到达率不固定的情况，即不确定公交需求的情况下的车辆控制策略，以实现根据需求合理安排公交发车，实现公交资源优化配置，进一步提高服务水平和运营效率。