熔喷气流场与纤维运动及纤维直径的数学计算
2019-01-14谢胜应英方海素申屠宝卿
谢胜 应英 方海素 申屠宝卿


摘 要:对狭槽模头下熔喷气流场进行了数值模拟,得到气流的流线以及速度矢量分布,采用高速摄像技术捕捉狭槽喷嘴下的纤维运动轨迹,并对纤维运动的特征及其与气流场特征之间关系进行探讨,结果显示纤维的二维运动特征是由气流场的二维特征决定的。因为熔喷过程中纤维运动速度很高,测量设备很难在线测量熔喷过程中的纤维直径的变化规律,本文建立了一种可以计算纤维直径的数学方法,该方法只凭借纤维轨迹信息就能在线计算纤维直径的变化规律。首先对这种数学方法做统一的理论推导,之后在理论推导基础上对纤维模型进行离散处理,经过离散处理后可得到更精确的数学解,将数学预测的结论与实验获得的纤维直径进行对比,结果表明数学预测与实验结论较为吻合。
关键词:熔喷;气流场;纤维运动;纤维直径;数值模拟;数学预测
中图分类号:TS101;TS151
文献标志码:A
文章编号:1009-265X(2019)05-0015-06
Abstract:The melt-blowing air flow field under slot-die was numerically simulated, and the flow line and velocity vector distribution of air flow were gained. Fiber motion path was captured by high-speed photography technology, and the relationship between air flow field features and fiber motion features was discussed. The results showed that two-dimensional motion feature of fibers was determined by corresponding two-dimensional characteristics of air flow field. Since fiber velocity in melt-blowing process was high, online measurement of fiber diameter change rule in the melt blowing process by measuring equipment was unrealizable. In this study, a mathematic method was built to calculate fiber diameter, which can calculate fiber diameter change rule on line just according to the fiber path information. Firstly, the unified theoretical derivation was accomplished, and then discrete treatment was conducted for the fiber model on the basis of theoretical derivation. After disperse treatment, more precision mathematic solutions could be gained. The mathematically predicted conclusion was compared with the fiber diameter acquired by the experiment. The result showed that the mathematic prediction is consistent with the experimental conclusion.
Key words:melt blowing; air flow field; fiber motion; fiber diameter; numerical simulation; mathematic prediction
熔喷技术制备微米级纤维非织造布材料过程中,聚合物熔体经过高温熔融挤出、高速空气牵伸而形成微米级纤维[1]。熔喷非织造布的纤维直径在1~5 μm,属于超细纤维,使得熔喷非织造布材料在医疗卫生、过滤净化及保暖等领域有着重要的应用[2]。
目前对于熔喷技术的研究集中在两大方面,一是关于熔喷气流场的研究,二是熔喷过程中纤维运动的研究。Shambaugh团队对熔喷气流场进行了系统的数值模拟研究[3-5]和实验测量研究[6-7],Xie等[8]对螺旋形模头熔喷气流场进行了数值模拟。相对于气流场的研究,针对纤维运动的研究相对较少,Chhabra等[9]以及Yin等[10]在低速條件下对纤维运动进行了初步的探索。本文对熔喷气流场进行数值模拟研究,利用高速摄像技术对熔喷过程中纤维的运动规律进行定性研究。
熔喷过程中,纤维的直径变化信息非常重要,因为纤维直径的变化直接反映了气流对纤维的拉伸作用,而气流对纤维的拉伸作用正是熔喷技术制备微米级非织造材料的核心内容。聚合物熔体纤维从模头的喷丝孔挤出后继续保持熔融状态,熔体纤维在高速湍流场的吹喷作用下运动十分剧烈,使得在线测量纤维直径也变得异常困难[9-10],也导致对于纤维直径的变化规律研究大部分研究集中在理论推导,缺乏实验验证。
针对以上问题,笔者提出了一种仅凭借已知纤维轨迹信息即可实现对纤维直径在线求解的数学方法。这种数学方法不受实验测量的限制,是从纤维轨迹形貌为基础来计算纤维直径。首先对这种数学方法做一系列推导,之后对数学模型中的纤维模型施加离散处理,施加离散处理的原因是第一步推导出的数学方法具有一定的弊端,而经过离散处理后能消除以上弊端且能得到较为精确的数学解,数学预测得到的纤维直径与利用熔喷和静电两种纺丝实验获得的纤维直径进行验证,结果表明此数学方法在计算纤维直径变化规律方面具有一定的可行性和适用性。
1 熔喷技术与实验条件
1.1 熔喷技术
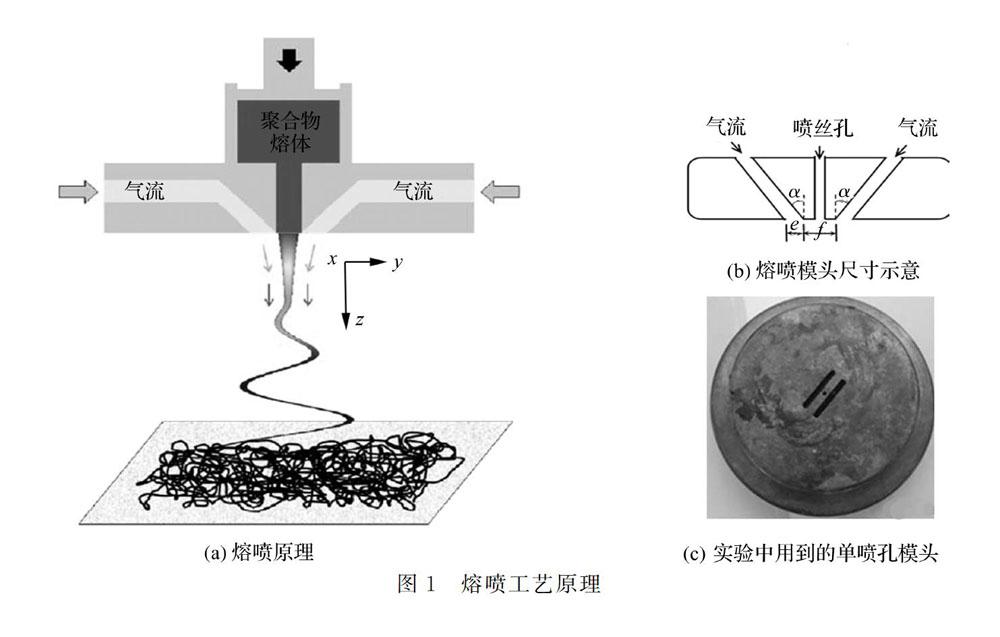
熔喷是一步法生产微米级纤维非织造布的方法之一。熔喷工艺如图1(a)[11]所示,从料斗注入的聚合物颗粒状原料经过高温螺杆的加热与挤压作用形成聚合物熔体,熔体经过计量泵的定量输出并从喷丝孔挤出,挤出后的熔体经高温、高速气流的吹喷作用而拉伸成超细纤维。
1.2 实验设备与条件
实验用到的模头类型为工业用单孔狭槽型模头,如图1(b)所示,具体尺寸为:鼻尖宽度(f)为1.28 mm;狭槽夹角(α)为30°;狭槽宽度(e)为0.65 mm;狭槽长度为6 mm;聚合物喷孔孔径为0.42 mm。图1(c)是实验用到的实际模头外观图。
熔喷实验中用的聚合物原料为聚丙烯(韩国SK公司),熔融指数为650 g/10 min。实验过程中,聚合物流量为7.8 cc/min;聚合物温度为260 ℃;气流温度为260 ℃;空压机施加的气流压力范围为5.1×104~12.7×104 Pa,因为高于12.7×104 Pa,纤维运动剧烈,超出了高速摄影机的捕捉能力。
在纤维轨迹的实验研究中,采用了HG-100K型高速摄像机(Inc., San Diego, USA),最大拍摄帧数为100 000帧/s。图像采集用到的是Nikon镜头,焦距24~85 mm。
2 气流场数值模拟与纤维运动
2.1 气流场的数值模拟建模
熔喷气流场的数值模拟模型是在GAMBIT 2.4下建立,数值模拟计算是在FLUENT 6.3下完成。
将模拟狭槽喷嘴下的区域定为:x[-6 mm,6 mm],y[-10 mm,10 mm],z[0,50 mm]。如图2(a)所示,可以看出模型关于x-z平面以及y-z平面都是对称的,这里只需要模拟1/4个流场区域并运用FLUENT自带的对称面设定功能即可实现对整个流场的模拟。图2(b)就是实际模拟的1/4流场区域,即模拟计算区域为:x[0 mm,6 mm],y[-10 mm,0],z[0,50 mm]。FLUENT 6.3模拟过程中,用到了雷诺应力湍流模型,湍流系数C1ε和C2ε分别设置成1.24和2.05[12]。
2.2 气流场结果分析
图3显示了数值模拟得到的狭槽喷嘴气流场流线图以及速度矢量图,两股气流从狭槽喷出后,经历了单独运行、相互接触以及融合过程[9],在这几个过程中,气流总体沿着平行于z轴的运动规律向下运动,图3(b)更加清晰地展示了以上3个过程,这也是为什么狭槽型熔喷气流场可以看做是二维流场的原因。值得注意的是,图3(b)展示了在模头下方,两股气流相互接触之前存在着气流的回流现象。目前为止,回流现象未得到实验证实。
2.3 纤维运动结果分析
图4展示的是在模头下方,不同压力的空气吹喷条件下的熔体纤维轨迹。可以看出,在低气压下纤维几乎是垂直向下运动的。随着气压的逐步提高,纤维的运动规律逐渐明晰。在相同的气压条件下,纤维的运动轨迹在y-z平面上的运动振幅(图4(a)-(d)所示)明显大于在x-z平面上的运动振幅(图4(e)-(h)所示),说明在狭槽型模头熔喷过程中,纤维的运动轨迹从截面上来看不是圆形结构,而是近似于椭圆的结构,这个现象与气流场的二维特征相符。
3 纤维直径的数学预测
3.1 数学方法的提出
在熔喷过程中,原料出现裂解、气化等状况的几率几乎为零,因此若不考虑以上因素,那么纺丝前的原料体积等于纺丝后纤维的体积,可得:
3.2 直径的离散化处理
式(9)推导出了纤维直径变化规律的数学表达式,但是通过式(9)得出的结果有如下弊端:当随着t的增加(纤维运动一段距离后),纤维的直径df会将t时间段内的纤维直径平均计算,在宏观上表现为:跟着t的增加,实际的较计算得到的纤维直径会偏小。为了解决这个弊端,将纤维直径做离散处理,如图5所示,离散处理的做法是:将t分割成若干个时间片段Δt,这里的Δt也称为离散时间。在计算过程中,每个Δt內纤维直径单独计算,每次计算的结果不受前面算过的纤维直径的影响。经过离散化处理后,式(2)就转化为:
在离散计算时候,设离散时间Δt=10-4 s。其经过离散处理后数学方法求得的纤维直径随着纺丝距离z的变化规律如图6所示,可以看出:用数学方法求得的纤维直径随着纺丝距离的增大而迅速减小,其趋势与Rao等[13]理论推导的趋势一致。从图6中还可以得到,用数学方法和实验方法获得的纤维直径较吻合。值得注意的是,实验中,纤维是用水浴方法接收获得,用水浴接收原因是:在喷丝孔附近区域,纤维是熔融状态且速度较高,直接用接收帘子接收纤维会严重粘连使得线下测量无法实现,越接近喷丝孔,纤维粘连程度越高,采用水浴接收方法,纤维可以迅速降温固化,降低粘连效应,25 mm是可以接收到独立纤维的极限距离,若接收距离小于25 mm,接收帘子接收到的纤维是熔融粘结状态,无法得到独立纤维。这也解释了图6中z=25 mm处实验得纤维直径较数学方法得纤维直径有一定差别,而在z=50 mm处差别较小的原因。
3.3.2 静电纺丝实例验证
静电纺丝过程中,纤维的直线部分、螺旋部分以及无序部分构成了整个的纤维轨迹[14-15],图7展示了静电纺丝过程中纤维轨迹的3个部分,本次验证利用了纤维的直线部分。
验证用到的静电纺丝纤维直线轨迹数据信息来源于Reneker等[14]的实验数据,Reneker等用摄像机拍摄了静电纺丝过程中纤维的直线段,并用粒子跟踪法测量了直线段纤维点的运动速度,根据Reneker团队提供的实验数据,将静电纺丝中纤维速度与纺丝距离z之间的关系进行回归分析,得到:
同樣的,设离散时间Δt=10-4 s。图8展示了经离散处理后,数学方法求得的纤维直径及Reneker等[14]测量的纤维直径随纺丝距离z的变化规律,图8显示:本数学方法与实验获得的纤维直径具有很高的吻合度,也说明本数学方法在求解直线轨迹的纤维直径精确度最好。本数学方法较“最小二乘法”数值回归的典型区别在于纤维直径的获得基于真实的纤维轨迹数据,结果是唯一的而不是拟合的,本数学模型不会使用大量的数据来做回归预测,而是精确计算唯一解。
4 结 论
采用数值模拟方法模拟了狭槽型模头熔喷的气流场,并对熔喷过程中的纤维运动进行了高速摄像技术的捕捉,针对纺丝过程中,尤其在模头附近纤维直径的变化规律在线测量尤为困难的情况,本文建立了一个在线计算纤维直径的数学方法,得到如下结果:
a)数值模拟结果显示,狭槽型模头熔喷气流场中,气流经历了单独运行、接触和融合过程,并且气流场具有二维分布特征。
b)在狭槽型模头熔喷过程中,纤维的运动轨迹截面不是圆形而是椭圆形结构,也具有一定的二维特征,这与熔喷气流场特征一致。说明气流场特征决定了纤维的运动特征。
c)通过提出的数学方法,分别预测了熔喷和静电纺丝过程中纤维直径随着纺丝距离的变化,并借助一定的实验来验证,验证的结果表明,本数学方法对于纺丝过程中的纤维直径预测是一种有效的手段,并且针对近似直线轨迹的纤维直径预测精确度最高。
参考文献:
[1] 柯勤飞,靳向煜.非织造学[M].上海:东华大学出版社,2010:284.
[2] 许川,杨成帅.熔喷非织造喷射流场研究进展[J].现代丝绸科学与技术,2011,26(4):158-160.
[3] KRUTKA H M, SHAMBAUGH R L, PAPAVASSILIOU D V. Effects of die geometry on the flow field of the melt-blowing process[J]. Industrial & Engineering Chemistry Research, 2003,42:5541-5553.
[4] KRUTKA H M, SHAMBAUGH R L, PAPAVASSILIOU D V. Effects of temperature and geometry on the flow field of the melt blowing process[J]. Industrial & Engineering Chemistry Research, 2004,43:4199-4210.
[5] KRUTKA H M, SHAMBAUGH R L, PAPAVASSILIOU D V. Analysis of multiple jets in the schwarz melt-blowing die using computational fluid dynamics[J]. Industrial & Engineering Chemistry Research, 2005,44:8922-8932.
[6] UYTTENDAELE M A, SHAMBAUGH R L. The flow field of annular jets at moderate reynolds numbers[J]. Industrial & Engineering Chemistry Research, 1989,28(11):1735-1740.
[7] MOHAMMED A, SHAMBAUGH R L. Three-dimensional temperature field of a rectangular array of practical air jets[J]. Industrial & Engineering Chemistry Research, 1994,33:730-735.
[8] XIE S, ZHENG Y S, ZENG Y C. Air flow field and fiber motion in a swirl-die melt blowing process[J]. Advanced Materials Research, 2013, 690-693:2861-2865.
[9] CHHABRA R C, SHAMBAUGH R L. Experimental measurements of fiber threadline vibrations in the melt-blowing process[J]. Industrial & Engineering Chemistry Research, 1996,35:4366-4374.
[10] YIN H, YAN Z Y, BRESEE R R. Experimental study of the meltblowing process[J]. International Nonwovens Journal, 1999,8(1):60-69.
[11] CHUNG C, KUMAR S. Onset of whipping in the melt blowing process[J]. J Non-Newtonian Fluid Mech 192:37-47.
[12] KRUTKA H M, SHAMBAUGH R L, PAPAVASSILIOU D V. Analysis of a melt-blowing die: comparison of cfd and experiments[J]. Industrial & Engineering Chemistry Research, 2002,41:5125-5138.
[13] RAO R S, SHAMBAUGH R L. Vibration and stability in the melt blowing process[J]. Industrial Engineering Chemistry Research, 1993,32(12):3100-3111.
[14] RENEKER D H, YARIN A L. Electrospinning jets and polymer nanofibers[J]. Polymer, 2008,49:2387-2425.
[15] RENEKER D H, YARIN A L, FONG H, et al. Bending instability of electrically charged liquid jets of polymer solutions in electrospinning[J]. Journal of Applied physics, 2000,87(9):4531-4547.
