基于改进Kriging插值的煤矿井下定位算法

朱恒军, 王冠钰, 张 靓

( 1. 齐齐哈尔大学 通信与电子工程学院，黑龙江 齐齐哈尔 161006; 2. 黑龙江交通职业技术学院 铁道机车学院，黑龙江 齐齐哈尔 161000 )

0 引言

掌握井下人员、车辆、设备的位置信息不但利于煤矿企业高效生产，而且能在发生矿难时快速施救，减少损失[1]。传统的射频识别定位技术已不能满足井下定位在精度、稳定性、效率方面越来越高的要求。无线传感器网络技术以能耗低、成本低、无线自组织通信、扩展性强等特点，在煤矿井下的定位应用逐渐成为研究热点[2]。

在与无线传感器网络定位技术对应的定位算法中，位置指纹定位算法具有受环境干扰小、精度高等优点，更加适合井下环境应用。在离线阶段构建位置指纹数据库时需采集大量位置指纹，以保证定位精度，耗费大量人力、物力。根据改进的路径衰减模型，Kubota R等估计位置指纹[3]； Racko J等运用线性和Delaunay插值对位置指纹进行估计[4]；Germán M等采用线性向量回归方法对位置指纹进行估计[5]。在环境干扰较小的情况下，这些算法对位置指纹的估计性能良好，且实现简单，但在井下巷道复杂环境下，位置指纹的估计精度大幅下降。刘辉元等采用距离倒数加权估计插值点位置指纹[6]；张梦丹等提出一种线性插值法重构离线指纹库[7]；刘文远等将整个室内环境划分为多个环路快速分割地图，获取射频指纹并构建位置指纹数据库[8]。根据采样点之间的相对位置关系，三种算法结合位置指纹对插值点进行估值，在井下复杂信号传播环境下，信号衰落不仅与位置有关，还受环境因素影响，位置指纹估计精度较低。王永星等提出一种基于Kriging插值算法的RSS指纹数据快速生成方法[9]，通过变异函数对信号传播环境进行描述，考虑环境影响，但在拟合变异函数时运用最小二乘法容易陷入局部最优。王红军等利用支持向量回归法拟合变异函数，提高插值精度。两种算法提高变异函数拟合精度，进而提高插值的精度[10]。

为解决井下定位中存在的逐点采集位置指纹工作量较大的问题，在保留Kriging空间插值优点的基础上，引入灰狼优化算法。首先通过采集的位置指纹构建实验变异函数，综合分组和差分进化策略对灰狼优化算法进行改进，优化变异函数参数的选取，提高由实验变异函数拟合理论变异函数的精度，进而提高对其它位置指纹估计精度和定位精度。在实现减少采集工作量目标的同时，实现通过采集部分位置指纹估计所有位置指纹的功能，以达到提升位置指纹的插值精度和井下定位精度的效果。

1 位置指纹匹配定位算法

因所处井下巷道不同位置，信号的多径结构不同，称每个位置独特的多径信号为位置指纹。定位过程包含位置指纹数据库构建和在线匹配定位[11]。基于位置指纹的匹配定位原理和流程见图1。

图1 基于位置指纹的匹配定位原理和流程Fig.1 Positioning fingerprint based on matching positioning principle and process

位置指纹数据库构建是在定位区域内设置若干基于位置指纹的匹配定位参考点，将每个参考点的实际位置和接收到的无线信号信息存入数据库[12]。因接收信号强度RSSI测量方便，无需额外硬件，大多选择记录RSSI。理论上，定位区域内的参考点越密集，目标定位精度越高。然而煤矿井下巷道狭长，干扰较多，为保证位置指纹定位精度不受影响，需大量部署参考点，耗费大量人力用于采集采样点位置指纹。

在线匹配定位阶段，将未知节点的位置指纹与数据库中的数据进行比较，寻找最相似参考点，用匹配定位算法计算未知节点位置。最常用的KNN定位算法，将欧氏距离最小的K个参考点位置坐标求取均值作为未知节点的位置坐标[13]。

在煤矿井下复杂环境中，将环境温度、湿度、粉尘，空间狭窄，管道纵横等因素对信号的干扰，作为位置指纹在定位中使用，以使算法抗环境干扰能力增强，工作更稳定，更适于井下定位。

2 构建位置指纹数据库

采用Kriging插值算法，在充分考虑区域化变量间的相关性后，对每一个区域化变量赋予一定的权重因数，最后进行加权平均估计预测区域[14]。受井下环境中多径效应对信号的影响，不能简单根据信号衰减模型计算RSSI值。Kriging插值算法既利于分析采样点和待估点的相对位置和RSSI值，又利于通过变异理论从整体信号空间变异结构角度，考量已知点间的关系及其对插值位置的影响，插值结果更准确、更符合真实环境。插值点RSSI值计算公式为

(1)

式中：Z*(x0)为插值点的RSSI值;Z(xi)为第i个参考点xi处的RSSI值;λi为第i个采样点对插值点的权重因数。Kriging插值算法的关键是计算权重因数。

通过变异函数描述空间距离为h的两个位置指纹之间的相关性，根据N个采样点位置指纹进行计算，则变异函数r(h)为

(2)

在实际应用中，很难得到所有点之间的变异函数，常采用采样点的变异函数对变异函数模型进行拟合，其中球状模型应用最为广泛，有

(3)

式中：C0、C和a为变异函数的参数，其中C0为块金值，C为偏基台值，a为变程。

在保证对待估点Z*(x0)的估计满足无偏性和最小方差性的情况下，解得权重因数为

λ=A-1γ0,

(4)

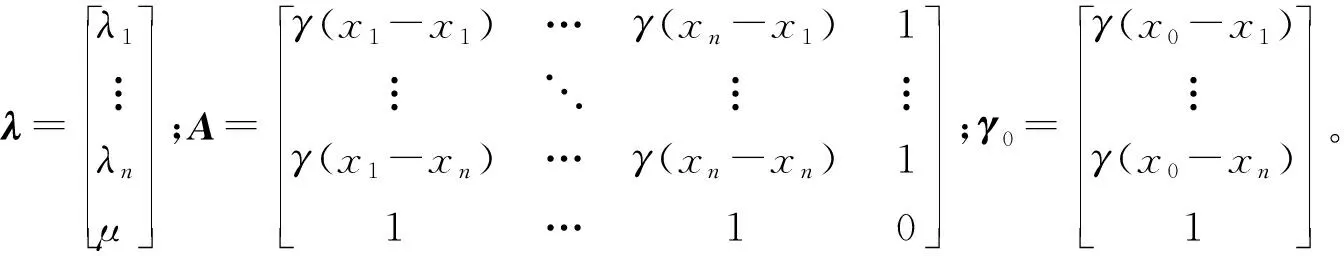
3 改进Kriging插值定位算法

3.1 普通灰狼优化算法

通过Kriging插值算法估计部分位置指纹可减轻采集工作量。由于位置指纹的估计精度影响井下定位精度，为进一步提升位置指纹估计精度，达到提高井下定位精度的目的，引入灰狼优化算法优化变异函数的C0、C和a三个参数。灰狼优化算法是由Mirjalili S等提出的、一种通过模拟灰狼的社会等级和狩猎行为的新型群体智能优化算法[15]。该算法具有结构简单、参数设置少、容易实现、收敛精度高和收敛速度快等特点。

灰狼优化算法实现步骤：

(5)

其误差越小，拟合效果越好。将灰狼按适应度值从小到大排序，前三名分别设置为α、β和δ狼，其余为ω狼。

(2)更新灰狼个体位置。由α、β和δ狼引导ω狼进行追捕猎物，即对每组解进行更新，有

(6)

(7)

(8)

式(6-8)中：t为当前的迭代次数;X(t+1)为更新后灰狼的位置;Dα、Dβ和Dδ分别为其它灰狼ω与α、β和δ的距离，且

Dj=|ClXj(t)-Xω(t)|,

(9)

其中j=α,β,δ；Al和Cl(l=1,2,3)的计算公式为

Al=2ar1-a,

(10)

Cl=2r2,

(11)

式(10-11)中：a从2线性递减到0；r1和r2为区间[0,1]的随机数。

3.2 改进灰狼优化算法

灰狼优化算法与其它贪婪算法一样，求解优化问题时易出现早熟、易陷入局部最优等缺陷[16]，提出综合分组策略和差分进化策略对灰狼优化算法进行改进。

首先，将整个灰狼种群按适应度排序分为两组。第一组适应度好的种群，按照灰狼优化算法对灰狼个体进行更新；第二组适应度差的种群，先采用差分进化算法对狼群进行变异，增强全局搜索能力，再进行灰狼优化。并且，随着迭代次数的增加，逐渐增大第一组种群的个数，逐渐减少第二组种群的个数。在迭代前期能够避免早熟和陷入局部最优，在迭代后期利于减少变异次数，提高搜索速度。

差分进化算法步骤:

(1)变异操作。在由变异函数的C0、C和a三个参数构成的灰狼种群中随机选取两个不同的灰狼，将其位置求差进行缩放后再与待变异的灰狼进行合成。第k个灰狼变异个体uk(t)为

uk(t)=Xp1+F(Xp2-Xp3),

(12)

式中：Xp1、Xp2、Xp3为灰狼种群中随机选择的三个不相同个体;F为[0,1]之间的缩放比例因子。

(2)交叉操作。将原有灰狼个体Xk(t)与变异后产生的个体uk(t)的第j个参数进行交换，增加种群的多样性，即

(13)

式中：CR为取值[0,1]之间的交叉概率；rand(m,n)是[m,n]上均匀分布的随机函数。

(3)选择操作。通过差分机制可保证子代个体至少不比当前个体差。选取适应度值较好的个体:

(14)

3.3 井下定位算法

通过优化的Kriging插值算法进行井下定位步骤:

(1)人工多次采集采样点位置指纹。通过高斯滤波剔除由环境干扰造成的异常值，可得比较稳定的位置指纹，并记录采样点的位置信息。

(2)将采样点的位置指纹和位置信息通过式(2)构建实验变异函数数据集。

(3)初始化灰狼个体位置，即C0、C和a三个参数，并计算每个灰狼个体的适应度值。根据适应度值将灰狼个体划分为两组：第一组适应度好的灰狼个体，按式(5-10)更新自身位置；第二组适应度差的灰狼个体，先按式(11-13)进行差分变异，灰狼个体再按式(5-10)更新自身位置。判断是否达到迭代次数，如果没有，则调整每组灰狼的个体数量，并且重复这一过程；如果达到迭代次数后，则输出C0、C和a三个参数。

(4)将C0、C和a三个参数代入式(3)，构建理论变异函数。

(5)根据式(1)、式(3)、式(4)估计插值点的位置指纹。

(6)采集井下人员的位置指纹，采用KNN匹配算法计算井下人员位置。

采用改进的灰狼优化算法，优化Kriging插值位置指纹井下定位算法流程见图2。

4 实验及结果分析

4.1 实验环境

实验区域选择长为80.0 m、宽为4.0 m，高为3.0 m的狭长通道模拟井下巷道环境。采用CC2530模块作为信标节点和未知节点，在通道两端和中心分别布置5个信标节点，距地面1.8 m，以实验区域的长、宽、高为坐标系的x、y、z轴。由于巷道长度远大于宽高，故宽高可忽略不计，在巷道中央每隔1.0 m设置一个采样点。每个采样点采样100次，将求取均值作为位置指纹实际值。采用MATLAB软件对算法进行测试，井下节点部署实验环境见图3。

图2 Kriging插值位置指纹井下定位算法流程Fig.2 Kriging interpolation location fingerprint downhole localization algorithm flow

4.2 实验结果

首先，分析不同数量的采样点，采用改进Kriging插值算法估计位置指纹的误差，定义相对估计误差e，即

(15)

分别从采样点集合中随机选取20%～80%数量的位置指纹估计剩余的位置指纹，计算RSSI估计误差，重复实验10次，将求取均值作为最终误差。为比较不同算法的插值性能和检验算法的改进效果，选择有代表性的IDW插值、普通Kriging插值和改进Kriging插值算法生成位置指纹的误差。不同算法生成RSSI位置指纹实验结果见图4。

由图4可知，随着已知位置指纹数量的增加，位置指纹估计误差逐渐减小，当位置指纹数量超过50%时，估计误差下降缓慢；改进Kriging插值算法估计误差小于普通Kriging插值算法的，也小于IDW插值算法的，表明改进Kriging插值算法可以提升位置指纹插值精度，更加接近实际采集值。

改进Kriging插值算法在不同数量采样点的位置指纹估计误差和运算时间见表1。由表1可知，当采样点数量超过50%时，估计误差下降缓慢，但算法的运行时间即运算量不断增加，因此选择采集50%的位置指纹估计剩余的位置指纹。

当采样点数量为50%时，比较随机选取采样点与隔点均匀选取采样点对位置指纹估计的影响，实验结果见表2。由表2可知，相对于随机采样，均匀采样位置指纹估计误差更小，并且采用改进Kriging插值算法时，隔点采集50%位置指纹估计剩余50%位置指纹估计误差最小。

表1 改进Kriging插值算法估计误差与运算时间

图3 井下节点部署Fig.3 Underground node deployment

Table 2 Influence of different sampling methods on relative estimation error%

其次，分析不同插值算法对定位精度的影响。选择节点估计坐标与节点实际坐标间距离的均方根误差E作为评判标准，有

(16)

分别采用IDW插值、普通Kriging插值、改进Kriging插值算法和逐点采集位置指纹，构建位置指纹数据库，在定位区域内，随机采集50个未知节点的位置指纹，采用KNN算法进行定位并计算定位误差。重复实验20次，将求取均值作为最终误差。4种算法的定位结果见图5，定位误差结果见表3。

图4 不同算法生成RSSI位置指纹误差Fig.4 Different algorithms generate RSSI fingerprint error

图5 不同算法的定位结果Fig.5 Localization results of different algorithms

误差类别逐点采集改进Kriging插值普通Kriging插值IDW插值平均误差/m2.552.723.033.27误差方差0.870.951.051.86

由图5和表3可知，改进Kriging插值算法定位误差最接近逐点采集构建数据库定位误差，相比于普通Kriging和IDW插值算法，改进Kriging算法进一步提升定位精度，且误差波动最小，定位性能更加稳定。在采用隔点采集位置指纹情况下，通过改进Kriging插值算法构建完整位置指纹数据库定位性能，最接近逐点采集构建位置指纹数据库，在节省位置指纹采集工作量的同时，相对于普通Kriging和IDW插值算法，其插值精度和定位精度有大幅提升。

5 结论

(1)在采集部分位置指纹的基础上，首先利用Kriging插值算法估计全部位置指纹；然后改进灰狼优化算法，优化Kriging插值算法的变异函数参数；最终提出基于改进Kriging插值的煤矿井下定位算法。

(2)该算法在定位时只需隔点采集位置指纹，就可以估计全部位置指纹，提高位置指纹的采集效率，与普通Kriging和IDW插值算法相比，改进Kriging插值算法提升位置指纹估计精度和定位精度，更加适合在煤矿井下定位过程中应用。