双重介质致密分形气藏水平井压力动态分析

张春光， 姜瑞忠， 乔 欣， 崔永正， 沈泽阳， 张福蕾， 原建伟

( 1. 中国石油大学(华东) 石油工程学院，山东 青岛 266580； 2. 中国石油北京油气调控中心，北京 100007 )

0 引言

研究双重介质致密分形气藏的渗流特征，需要充分考虑致密基质块的非线性渗流、启动压力梯度及裂缝的应力敏感性、分形特征等因素，应用达西渗流理论描述该类储层存在局限性[1-3]。

基于Warrant-Root模型，何国良[4]、同登科等[5]建立双重介质渗流模型，分析压力对具有分形特征的孔隙度和渗透率的影响。宋付权[6]考虑启动压力梯度和介质变形，推导低渗透油藏的产能公式并研究产量递减规律。姜汉桥等[7]建立不完全可逆变形介质的渗流模型，釆用全隐式和Richtmyer线性化方法对模型进行数值求解。李允等[8]认为低渗透气藏存在启动压力梯度，在特定压力范围内，渗流速度与压力梯度呈非线性关系。孙贺东等[9]根据裂缝性应力敏感气藏的实验数据和试井理论，引入渗透率模量，建立渗透率呈指数形式变化的双重介质试井模型。Zhang L等[10]考虑压力变化对孔隙度和渗透率的动态影响，建立第二类边界条件下可变形双重介质分形气藏的非稳态流数学模型，基于分形理论，证明模型存在收敛的有限元离散数值解。姜瑞忠等[11]分析低渗透储层非线性渗流的微观机理，引入屈服应力和边界层流控制的非线性参数，以Hagen-Poisseuille定律为基础，推导得到低速非线性渗流模型。基于质量守恒原理和达西定律，Rao L等[12]建立双孔介质—三线性流动模型，分析双重孔隙参数、裂缝流动能力、二次梯度项和表皮因数对量纲一的压力的影响。Razminia K等[13]应用分形几何和分数阶微分的概念，研究双区复合储层压力的数学解析方法。Amin D等[14]利用瞬态产量递减分析估算，提出计算天然裂缝性储层平均压力的方法，与物质平衡法得到的结果一致。刘建军等[15]根据复杂学科的多尺度关联方法及多尺度裂缝建模的相关文献，提出储层中多尺度裂缝的分级标准,分析连续介质和离散介质构建的代表性模型。

人们研究双重介质致密气藏的压力特点，简化储层的渗流模型，但不能充分体现双重介质致密气藏的特点。笔者考虑该类储层的裂缝分形特征、致密基质块的非线性渗流机理及渗透率各向异性，建立双重介质致密分形气藏水平井非线性渗流模型，利用等价压力点处理模型内边界条件，基于有限元原理求解井底压力，绘制井底压力动态曲线，对比不同模型渗流规律并对相关参数进行敏感性分析。

1 渗流机理

1.1 裂缝分形特征

达西渗流理论基于欧式空间，描述储层裂缝的复杂性与非均质性具有局限性。引入分形理论，利用分形维数及异常扩散系数表征分形裂缝的渗透率和孔隙度，使模型更精确地描述实际储层的裂缝形态[16]。

令分形体内流体储集在某节点处且每处节点体积相同，由节点的密度得出渗流节点的数量α为

(1)

式中：Df为裂缝分形维数；ds为谱维数；μ为流体黏度；rw为井筒半径；kfw为生产井处的渗透率；φfw为生产井处的孔隙度；Cft为裂缝综合压缩系数。

用d表示分形体嵌入岩块的欧式维数，则裂缝孔隙度φf为

(2)

式中：B为描述对称性的几何常量；Vs为储集流体的节点体积；Vf为裂缝孔隙体积；V为储层总体积；r为距生产井的距离。

裂缝孔隙度主要受孔隙空间的聚集方式(可用分形维数表征)影响，与有效上覆压力呈指数关系。引入裂缝压缩系数Cf，考虑应力敏感性的分形孔隙度φf(r)为

(3)

式中：mi为原始地层拟压力；mf为裂缝系统拟压力。

裂缝之间的连通性(可用异常扩散系数表征)影响裂缝渗透率。Pedrosa O A研究应力敏感地层不稳定试井，证明渗透率与基岩上覆压力呈指数关系[17]。引入异常扩散系数θ，考虑应力敏感性的分形渗透率kf(r)为

(4)

式中：γm为渗透率模数。

1.2 基质非线性渗流

低渗透储层研究常用模型为拟启动压力梯度模型、分段模型及连续模型。3种模型基于渗流实验，由不同函数拟合实验数据所得，由于物理背景不丰富，很难解释低渗透储层启动压力梯度和非线性渗流产生的根本原因。笔者在低渗透储层微观渗流机理及毛管渗流模型的基础上，改进并简化低速非线性渗流模型。

考虑启动压力梯度及非线性渗流，在Hagen-Poisseuille定律的基础上进行修正可得

(5)

式中：ν为通过岩心的流速；K为岩心渗透率；r0为毛细管半径；δ为表边界层厚度；τ0为表流体屈服应力；p为压力梯度。

同一根毛管，压力梯度越大，边界层越薄，即δ/r0与压力梯度成反比关系，令δ/r0=a1/p；同一种流体屈服应力不变，令8τ0/3r0=a2(a1、a2为实验数据拟合所得常数)。式(5)变形并简化为

(6)

(7)

式中：c1、c2为实验数据拟合所得非线性参数,c1反映流体的屈服应力及边界层对渗流的影响，c2主要反映边界层对渗流的影响。

当c1=0时，式(7)为达西模型；当c2=0时，式(7)为拟启动压力梯度模型，c1/(p-c2)为启动压力梯度项。

令ν≥0，满足p≥c1+c2，则最小启动压力梯度为pmin=c1+c2。当c1+c2=0时，pmin=0，即渗流不存在启动压力梯度；当c1+c2>0时，pmin>0，渗流存在启动压力梯度，式(7)变形为

(8)

此时，渗流曲线不通过原点，随压力梯度增大曲线趋于直线，即压力梯度增大到一定程度，所有孔喉参与流动，边界层厚度不再发生变化开始出现拟线性流。拟线性流段的反向延长线与横轴的交点即启动压力梯度。

2 渗流模型

2.1 物理模型

双重介质致密分形气藏水平井物理模型见图1。假设条件：

(1)模型由基质系统和裂缝系统组成，是基质系统向裂缝系统发生拟稳态窜流的双孔单渗的圆形气藏；

(2)外边界封闭或定压，储层厚度为h，地层拟初始压力为mi，水平井半长为L，气藏半径为re；

(3)水平井位于气藏平面中心，地面产气量为qsc；

(4)考虑储层的表皮因数、井筒储集系数及渗透率的各向异性，裂缝水平渗透率为Kfh，裂缝垂直渗透率为Kfv，基质系统渗透率为Km；

(5)考虑裂缝系统的应力敏感性和分形特征，以及基质向裂缝系统的非线性渗流；

(6)忽略重力与毛管压力的影响。

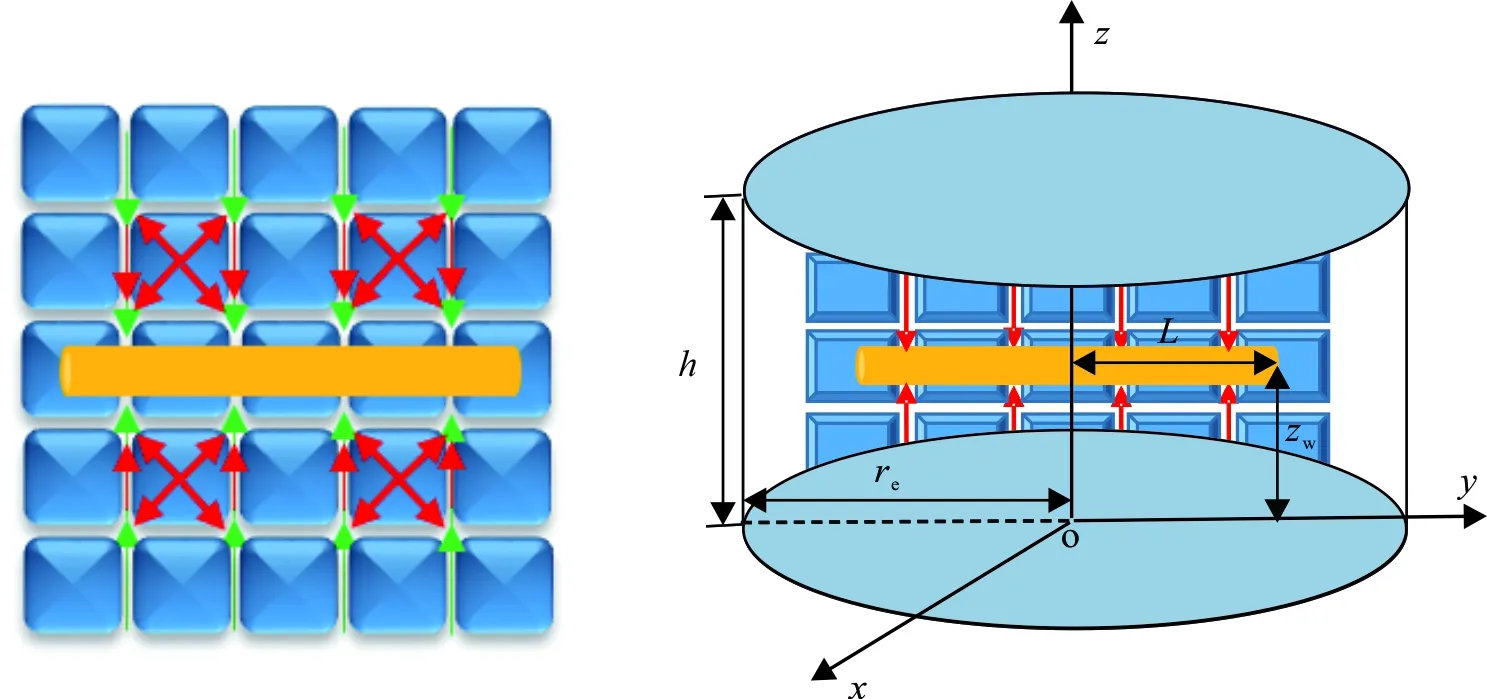
图1 双重介质致密分形气藏水平井物理模型

2.2 数学模型

2.2.1 模型建立

在圆柱坐标系下，运动方程式(7)结合质量守恒方程及状态方程，考虑储层应力敏感性，得到双重介质致密分形气藏水平井非线性渗流模型[18-19]：

(9)

(10)

限制条件：当mfD-mmD<(c1D+c2D)/2时，δLVD=0；当mfD-mmD≥(c1D+c2D)/2时，δLVD=1-c1D/[2(mfD-mmD)-c2D]。

初始条件为

mfD|tD=0=mmD|tD=0=0。

(11)

内边界条件为

(12)

式中：zwD、εD分别为量纲一的水平井纵向坐标和微变量。

封闭外边界条件为

(13)

(14)

式中：reD为量纲一的泄流半径。

定压外边界条件为

mmD(rD=reD)=mmD(zD=0,1)=0;

(15)

mfD(rD=reD)=mfD(zD=0,1)=0。

(16)

2.2.2 模型求解

对双重介质致密分形气藏水平井模型，采用隐式方法求解裂缝系统、显式方法求解基质系统。

应用Galerkin法得到裂缝系统的有限元方程(不存在源汇项时)为

(17)

式中：Ni为形函数，i=1,2,…n。

以格林公式为基础，通过分部积分得到内部单元和封闭条件外边界单元的有限元方程为

(18)

裂缝系统单元有限元方程的矩阵形式为

(19)

对矩阵方程化简得

(20)

式中：Ke为非线性系数矩阵；Fe为单元载荷向量；n为时刻变量。

式(20)中的Ke、Fe表达式为

(21)

(22)

同理，基质的有限元矩阵方程化简得

(23)

式(23)中的Ke、Fe表达式为

(24)

(25)

式(20)和式(23)分别为裂缝系统和基质系统的有限元单元平衡方程。根据基质场的上一时刻值求解裂缝场的压力解，再将该时刻裂缝场压力解引入基质场求基质压力解。

模型求解过程中需要处理水平井的内边界条件，无限导流能力模型符合水平井的实际情况，考虑无限导流能力模型比均匀流量模型求解困难，选取0.7L处为水平井在两种模型下的等价压力点，利用均匀流量模型评价水平井的井底压力[20]。

将水平井考虑为单元内源汇项并积分，应用Delta函数将水平井划分n个节点，得到量刚一的单元源汇项有限元方程为

(26)

考虑井筒储集效应与表皮因数，利用Duhamel原理并对压力解进行Laplace变换得

(27)

式中：S为表皮因数；s为Laplace变量；CD为井筒储集系数。

采用Stehfest数值反演方法，得到考虑井筒储集效应与表皮因数的水平井井底拟压力解为

(28)

(29)

3 数值模拟

3.1 模型对比

双重介质致密气藏水平井的达西模型、非线性模型及分形非线性模型的拟压力及压力导数曲线见图2。其中：CD=100，S=0，ω=0.02，λ=10-5；对于达西模型，γmD=0.02，cD=0，θ=0，Df=2.0；对于非线性模型，γmD=0.02，cD=0.5，θ=0，Df=2.0；对于分形非线性模型，γmD=0.02，cD=0.3，θ=0.2，Df=1.9。设非线性参数cD=c1D=c2D，分形指数β=2+θ-Df。考虑应力敏感性越强，曲线末端上翘幅度越大[21-22]。

根据曲线形态，将双重介质致密气藏水平井渗流划分7个流动阶段，不同模型在各流动阶段的试井曲线呈不同形态，流动阶段划分及模型对比见表1。

表1 流动阶段划分及模型对比

3.2 敏感性分析

对非线性参数cD、水平井长度LD及分形指数β进行敏感性分析。

非线性参数对压力动态曲线的影响见图3。由图3可见，非线性参数主要影响基质向裂缝系统的窜流强度及出现时间。随非线性参数的增大，窜流的非线性增强，窜流强度减弱且窜流段出现时间延迟，在拟压力导数曲线上表现为下凹段右移且下凹程度减小，非线性参数不影响基质向裂缝窜流的结束时间。

水平井长度对压力动态曲线的影响见图4。由图4可见，随水平井长度的增加，早期径向流阶段越明显，早期线性流阶段曲线的斜率越大，且不同长度水平井的拟压力导数曲线在中期径向流起点处相交。水平井增长延迟窜流出现的时间，不影响窜流持续的时间及强度。考虑储层应力敏感性与非线性渗流，不同长度水平井的拟压力导数曲线在末端不是汇聚成一条直线，而是上翘形成一簇平行线。

分形指数对压力动态曲线的影响见图5。由图5可见，初始阶段分形指数对曲线形态影响不明显，随时间的增加，各导数曲线在中期径向流的起点处相交。分形指数越大，中期径向流阶段后拟压力导数曲线上翘幅度越大。分形特征使压力波在储层中逐渐传播并形成动态边界，导致系统在径向流阶段后拟压力导数曲线上翘幅度逐渐增大，体现分形气藏的典型特征[23]。

图2 不同模型压力动态曲线对比Fig.2 Comparison of different models pressure dynamic curves

图3 非线性参数对压力动态曲线的影响Fig.3 Influence of nonlinear parameter on pressure dynamic curves

图4 水平井长度对压力动态曲线的影响Fig.4 Influence of horizontal well length on pressure dynamic curves

图5 分形指数对压力动态曲线的影响Fig.5 Influence of fractal index on pressure dynamic curves

4 结论

(1)引入分形理论描述裂缝系统的应力敏感性及分形特征，应用非线性渗流模型描述致密基质块的渗流特性，考虑启动压力梯度，建立双重介质致密分形气藏水平井非线性渗流模型。

(2)采用等价压力点方法处理内边界条件，利用有限元原理求解模型；绘制并对比3种模型的井底压力动态曲线，划分7个渗流阶段，即井筒储存、表皮效应过渡、早期径向流、早期线性流、中期径向流、基质向裂缝窜流及基质向裂缝拟径向流。

(3)非线性参数增大，拟压力导数曲线下凹段右移且下凹程度减小；水平井长度增大，窜流出现的时间延迟；分形指数越大，中期径向流段后拟压力导数曲线上翘幅度越大，各拟压力导数曲线在中期径向流的起点处相交。