随机场模型下相关距离及参数变异系数对边坡稳定可靠度的影响

盛建龙 杨 博 翟明洋

（1.武汉科技大学资源与环境工程学院，湖北武汉 430081；2.冶金矿产资源高效利用与造块湖北省重点实验室，湖北武汉430081）

边坡失稳问题一直是学者们所关注的领域，近些年来对边坡稳定性的研究也越发的成熟。土的结构十分复杂，因此，土的性质在空间上随着时间是不断地变化的，即土性的表现为空间各向异性。由于变化的不确定性，土体性质也会表现出不确定性，用确定性的方法很难反映这种随机的变化。边坡的不确定性得到了大量学者的重视，其中，杨继红等［1］在对黄河边坡进行可靠度分析时采用了随机场计算模型，总结出在边坡稳定性计算时，计算边坡失效概率并采用随机场计算模型更加合理；Griffiths［2］在进行边坡稳定性分析时，提出随机有限元强度折减法计算方法，并证明了计算方法的合理性；白桃等［3-7］采用Morgenstern-Price简明算法编制程序对边坡破坏概率进行了研究，总结出边坡在相同安全系数条件下，破坏概率也是可能不同的，即在判断一个边坡是否失稳时，计算可靠度会更加合理；薛亚东等［8-11］运用随机场理论，将随机场离散中的局部平均法与FLAC3D计算软件结合，总结出随机场计算模型中，相关距离对边坡稳定可靠度的影响在垂直与水平方向上比较时，垂直方向的影响更为显著；李典庆等［12-14］在研究中，采用随机场计算模型，比较了不同变异系数下的参数对失效概率变化的影响，总结出参数变异系数存在一定的变化范围，即参数的变异系数在随机场模型中也会对边坡失稳造成一定程度的影响。各种研究都对研究随机场做出了有益的推进，但是大多数的研究仅仅关注了相关距离对边坡稳定性的影响，而忽略了参数的变异性。本研究利用C++语言以及FLAC3D软件，实现边坡土体参数在空间分布上的随机性，在对边坡失效概率的分析中，考虑土体黏聚力变异系数以及随机场计算模型对结果的影响。

1 随机场基本理论

1.1 局部平均法

设X(t1,t2)为二维的连续性随机场，得到随机场模型，最重要的工作是要将变量之间的关系转换为数值来表示，也就是随机场的离散。设μ和σ2分别为随机场的均值与方差。可以将随机场划分为有限个矩形单元A,A1,A2,…建立随机场模型，即将随机数据离散到随机场的每个单元中，按照离散后随机变量与离散单元随机场的关系，随机计算模型的建立有很多方法，其中局部平均法以其对数据要求低，收敛快，精度高的优点得到广泛的应用。本文采用该离散方法进行各向异性随机模型的分析。随机场中，划分的每个单元边长可表示为T1T2、，就其中一个矩形单元A=T1T2为例，用此法计算随机场在局部单元A内的结果为

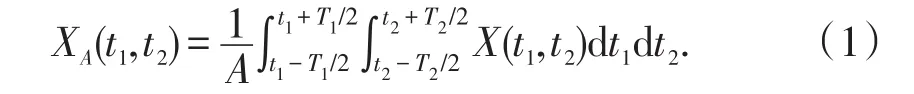
同理，可以算出各个单元的局部XA1(t1,t2),XA2(t1,t2),…。

设X(t1,t2)为一个稳定的空间随机模型。则对应局部单元的计算结果可以用各单元均值E[XA]、方差Var[XA]、协方差Cov[XA,XA1]等来近似表述。由式（1）可以得到用此法的计算过程中，并不会对原随机模型的均值有所改变，因此可以得到

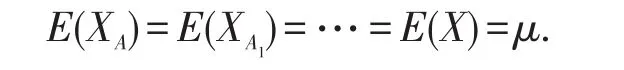
计算中，设γ(T1,T2)为X(t1,t2)的方差折减函数，为在随机场离散过程中造成的“点方差”σ2到“局部平均方差”的折减程度，则方差

同理，可以算出其他单元的方差。

A,A1为随机模型中2个单元，则协方差在这2个单元中可表示为

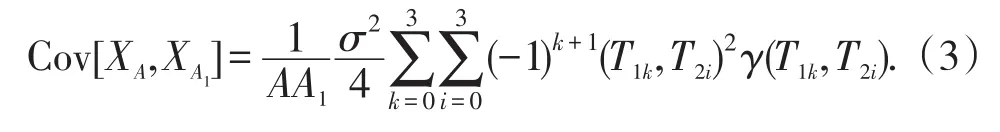
其中，T1k,T2i(k=0,…,3;i=0,…,3)所表示的意义由图1［15］所表示，γ(T1k,T2i)为方差折减函数。

1.2 相关距离

Vanmarcke［16］给出了如下关系来表示相关距离：

式中，T表示随机场空间中任意朝向的局部平均长度；γ(T)则为向量T所对应的方差折减函数。受相关性影响，土的结构性质在特定的范围里是基本相似的。超过此范围的土体之间，其性质大体没有联系。

1.3 相关函数

设ρ(τ1,τ2)，用来表示相关函数。其所表示的意义是随机场中的任意2个随机单元之间的土性参数的相关性。表1列举了在计算中比较常见的几种二维相关函数。

表1中，τ1,τ2表示随机场中任意2个单元所代表的坐标的水平以及垂直方向上的距离。可以用下式描述上述函数与各自方差折减函数之间的联系。

选取不同的函数对局部平均法的结果所带来的变化很小。表中所列举的以上表达方式有较大区别，但是所对应的方差折减函数在形式方面上差别实际不大［17］。因此，对随机模型记性分析计算时，相关函数采取简单的选取可以很大程度上简化过程。

按照一定的比例进行随机场的网格划分后，即可用协方差矩阵来表示每个网格之间的关系。从而根据统计参数的均值以及标准差对每个网格进行随机场数据的映射处理，形成随机场模型。

2 土性参数的空间各向异性

受到各种自然条件影响，土体特征理应为空间各向异性。Vanmarcke［18］首次提出了随机场模型，随后大量的学者对随机场进行了研究。一般来说随机场模型中用相关距离以及参数的变异系数表示，研究表明［19］，在空间中，水平方向上的相关距离对于垂直方向而言，要大很多。在垂直方向上，相关距离一般介于0.2～2 m之间。而在水平方向上，相关距离一般是介于20～80 m之间，有的甚至更大。参数变异系数一般用来表示不同数据之间的数值分散程度的大小，其定义为标准差和均值的比对于一般土坡，均值即使相同，其性质其实也有较大的差别，用变异系数来表征其中的区别程度会更加的合理。

由相关函数的表达式可以得出，当随机场中俩坐标的垂直与水平距离不相等时，即δ1≠δ2，根据上文中所表述的内容所建立的模型各土性参数的特征均表现为明显的空间各向异性。相比较于指数与高斯函数，可分离的指数函数所对应的方差折减函数更容易求得。上节中提到，对于相关函数的选取，局部平均法并不敏感。所以，为简化计算过程，减少计算量，对于模型的建立，所取的是可分离的指数函数。则有：

将式（7）代入式（5）则可以得到

3 随机场模型下边坡可靠度计算

对边坡失稳分析计算中，由于在随机场模型中，各个网格中的材料的赋予都是不确定的，因此用极限平衡法时，很难对边坡滑移面做出预先的确定。采取了有限元计算中的强度折减法进行分析，有效解决了上述问题。强度折减法就是：在边坡分析时，使其处于临界破坏状态，对其参数进行折减，以至使其失稳，相应数值软件自动根据计算结果得到安全系数。

对边坡进行分析时，采取了有限差分法对网格划分，并将响应面法与Monte-Carlo法相结合，其主要步骤如下：

（1）利用C++语言根据相关函数以及方差折减函数将随机场划分为均匀的矩形单元，生成协方差矩阵。本文为计算的简便，未考虑网格的划分对随机场模型下计算结果的影响，生成协方差矩阵。

（2）利用协方差矩阵和参数均值以及标准差，生成出随机场变量。

（3）在FLAC3D中将边坡进行有限差分，并根据局部平均法的坐标位置，将步骤（2）中生成的随机场变量赋予到有限差分网格中，完成对计算模型的建立。

（4）利用强度折减法对边坡进行有限差分计算，得到安全系数Fs并利用拉丁超立方抽样计算出响应面函数。

（5）结合Monte-Carlo法，利用响应面函数对边坡进行稳定计算，计算出实效概率Pf。计算流程见图2。

4 算例分析

以文献［2］中均匀土坡为例，采用本文所提方法进行分析。边坡坡比为1∶2，边坡高10 m，模型为20 m×60 m。土体饱和重度为20 kN/m3，土体弹性模量为100 MPa，泊松比为0.3，不排水抗剪强度为Cu（取φ=0）。为减少计算量，仅对黏聚力系数进行不确定性模拟，假设c服从对数正态分布，均值μc=0.25，标准差σc=0.125。

分析了在δx=30 m时，δy从1 m变化到10 m，与δy=2 m时，δx从5 m变化带80 m时，在不同黏聚力变异系数下其对边坡破坏所造成的影响。

利用边坡各条件，生成模型，并将其划分为1 m×1 m的规则网格。对随机场进行划分，如图3所示，为2 m×2 m的均匀矩形网格在有限差分网格中的映射，即建立的随机场模型图。

在FLAC3D中，利用强度折减法对边坡进行稳定性分析，图4所表示的为δx=30 m，δy=2 m时边坡失稳时的滑移面。

在δx、δy分别为30 m与2 m时，采用本文中的方法对失效概率进行计算，得到的结果Pf=0.032 6，对照文献［16］的结果0.035，绝对误差仅有0.002 4，相对误差仅有6%，说明所用研究理论是合理的。

图5反映了在垂直相关距离δy=2 m时，水平方向上在5～80 m变化时，对随机场模型下边坡失效概率的影响。分析比较得出，在相同变异系数条件下，水平相关距离越大，边坡破坏的几率也越大。在相同的水平相关距离条件下，黏聚力变异系数增大，边坡失稳的可能性同样也呈现出上升趋势，并且变异系数在0.1～0.4的上升过程中，失效概率的变化趋势比较平稳，δx=5 m时，变异系数由0.1上升到0.4，失效概率仅从0.002上升到0.003 4，增幅为0.001 4。而当从0.4变化到0.5时，失效概率由0.003 4上升到0.006 1，增幅为0.002 7，为0.1～0.4时的1.93倍。

图6反映了在δx=30 m，δy在1～10 m范围内变化时，对随机场模型下边坡失效概率的影响。从图中可以总结出以下结论：在参数变异系数相同时，随垂直相关距离增加，边坡发生失稳的可能性也会增大。相同垂直相关距离下，失效概率也随着黏聚力变异系数的增大而增加。变异系数在0.1上升到0.3的过程中，破坏概率的增加较为平缓，当变异系数由0.3增加到0.5，其数值呈现出显著增加趋势，尤其当δy在3 m以上时，这种变化尤为明显。在δy=10 m时，黏聚力变异系数由0.1增加到0.3时，失效概率由0.065上升到0.072，而黏聚力变异系数从0.3变化到0.5时，失效概率增加了0.08，为0.1～0.3的11倍以上。同样，对于垂直方向而言，其距离越大，在变异系数变化时，失效概率的变化程度越大。

通过分析比较图5和图6可知，在相同变异系数下垂直相关距离对边坡失稳可能性大小的影响远大于水平相关距离。在变异系数为0.5时，δx从5 m变化到80 m时，边坡的失效概率从0.68%上升到8%。对于垂直方向相关距离而言，当δy从1 m增加到10 m时，边坡失效概率由1.22%提升到15.21%。垂直相关距离的增幅仅为水平相关距离增幅的，而在失效概率上的增幅却是其2倍以上。在对2个图相关距离、变异系数变化曲线进行比较时，发现垂直与水平相关距离的差距并不明显，都呈现出一种上升趋势。垂直方向上，从变异系数为0.3开始，增幅有增大的趋势，而在水平方向上，这种趋势是从变异系数为0.4时开始的。在变异系数从0.1变化到0.3时，2个图的上升都较为平缓。

5 结论

基于局部平均法等随机场基本理论，采用C++语言编制了土体边坡随机场离散程序，在此基础上结合有限差分强度折减法及可靠度分析方法，研究了随机场模型的相关距离以及黏聚力变异系数对边坡可靠度的影响。所得结论如下：

（1）在相同变异系数下，通过比较相关距离在空间上的变化可以得出边坡失效概率在空间相关距离增大时呈现出一种上升的变化。

（2）在相同相关距离的条件下，通过变化曲线可以得出边坡失效概率由于变异系数的上升呈现出一种上升趋势。对于水平方向相关距离而言，变异系数在0.4以上时，这种变化趋势显著增大；对于垂直方向而言，变异系数在0.3以上时，这种变化表现出增大趋势。

（3）通过对空间中各方向上的相关距离对边坡失稳概率的变化程度进行比较分析。发现其在垂直方向上的影响程度远大于水平方向。

（4）对土性参数空间各向异性的研究还存在着许多不足之处。比如说，本文仅考虑了黏聚力系数的变化对失效概率的影响；同时建立的随机场模型只是黏聚力系数的单因素随机场，未考虑多因素随机场下对边坡失效概率的影响。