降雨条件下土石坝渗流稳定性研究

(广东省水利水电科学研究院 广东省水利重点科研基地，广州 510635)

0 引 言

我国是地质灾害频发国，土石坝失事即为其中一种。查阅文献可知，渗流是土石坝失事的主要原因之一[1]，而这种渗流往往都是饱和-非饱和渗流，它能够使非饱和土基质吸力迅速降低，从而造成失稳事故发生。目前，对饱和-非饱和渗流已有比较多的研究。Lu N等[2]基于非饱和渗流理论，利用数值模拟研究了煤岩质边坡在渗流作用下的稳定性，发现高孔隙水应力会影响到裂隙网络，使裂缝增多，入渗速率加快，有效应力降低，进一步导致煤岩边坡失稳。Oh S等[3]研究了基质吸力与体积含水率的变化对非饱和土坡稳定性的影响，得出非饱和渗流条件下的边坡稳定性与土体的渗流特性密切相关。陈善雄、陈守义[4]利用临界平衡法研究了非饱和土边坡的稳定性，得出饱和度影响基质吸力并进一步影响非饱和土体的抗剪强度的结论，对传统数值方法进行了改进。李兆平[5]等依据非饱和渗流理论，构建了一维瞬态含水率模型，并依据Fredlund提出的非饱和抗剪强度公式，推算出与基质吸力相关的安全系数公式，并应用于工程实例中。影响饱和非饱和渗流的外部因素主要是天然降雨，并受到多方面因素影响，如降雨雨型、降雨强度、降雨持时等[6-12]。本文将研究某土石坝在饱和-非饱和渗流作用下的稳定性分析，考虑到该土石坝所在地区气候较湿润，因此选择降雨工况进行研究。基于该地区雨季的平均日降雨量，进行相同降雨量下不同降雨强度与持时的土石坝渗流稳定性数值分析，结果可为土石坝渗流稳定性分析提供参考依据。

1 饱和-非饱和渗流基本方程

1.1 达西定律

达西渗透定律最先是由饱和土研究得来的。发现者为法国的工程师达西，他将均质土放置于圆筒，并进行渗透试验，得出结论：渗流断面间的渗流平均速度，与两断面间的水头差Δh成正比，与两断面间的渗径长度L成反比。这就是达西定律，它的表达式为：

(1)

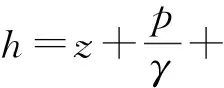
后来研究表明，达西定律也可以运用于非饱和土渗流。区别在于非饱和条件下，土体的渗透系数不再是常数，而是与含水率有关的一个变量，并且也与孔隙水压力的变化有关。

在达西定律中，v指的是达西流速，假设土体中流速为v′，其关系如下式：

v=nv′

(2)

其中n为孔隙率。

需要留意的是，达西定律仅适合研究层流渗流运动。而对于紊流渗流，则可用下式来描述:

(3)

式中：若m取1，则为层流；若m=2，则为完全紊流；若m取1到2之间，则为非完全紊流。

将式(3)变形，即可得到达西定律的空间表达式：

(4)

1.2 饱和非饱和渗流基本方程

图1为水流流过二维单元体时的渗流情况，取单元体厚度为dz。

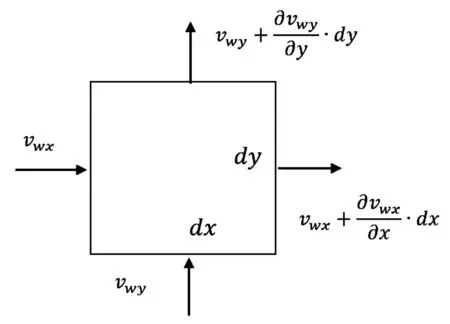
图1 二维单元体渗流图

从图1中可以知道，单位时间内，流入单元体中的水流体积为:

vwxdydz+vwydxdz

(5)

流出单元体的水流体积为:

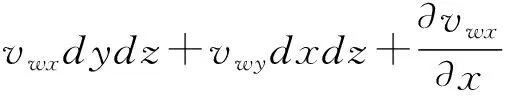
dxdzdy

(6)

于是两式做差，可得单位时间内流入流出的水量差为：

(7)

在dt时间段内，水量差为：

(8)

设θw为体积含水量，则单元体内水体积为θwdxdydz。根据质量量守恒，单元体内水的变化量应该等于流入流出水量差，因此得到下式：

(9)

由达西定律可知：

代入式(9)可得：

(10)

这就是非饱和土渗流的基本微分方程。

2 降雨入渗理论

降雨入渗理论是基于入渗率这个概念上的，入渗率代表土壤的入渗能力。Horton曾指出，降雨的入渗率会随着降雨持时的增加而越来越低。对于每一种介质而言，都可以用一条极限曲线来反映它每一时刻的最大入渗量，这条曲线与土体的饱和渗透系数有关。见图2、图3。

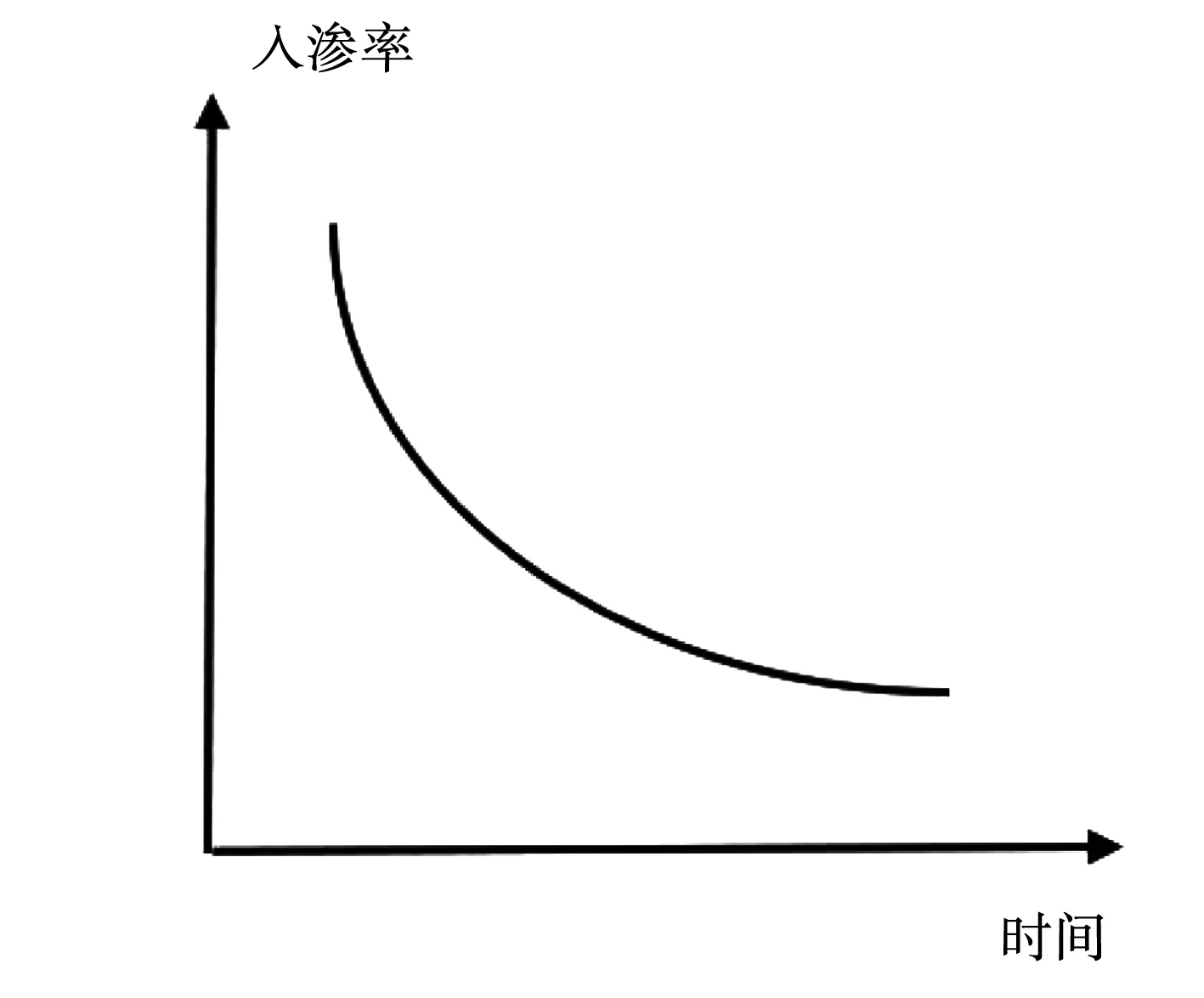
图2 最大入渗率图

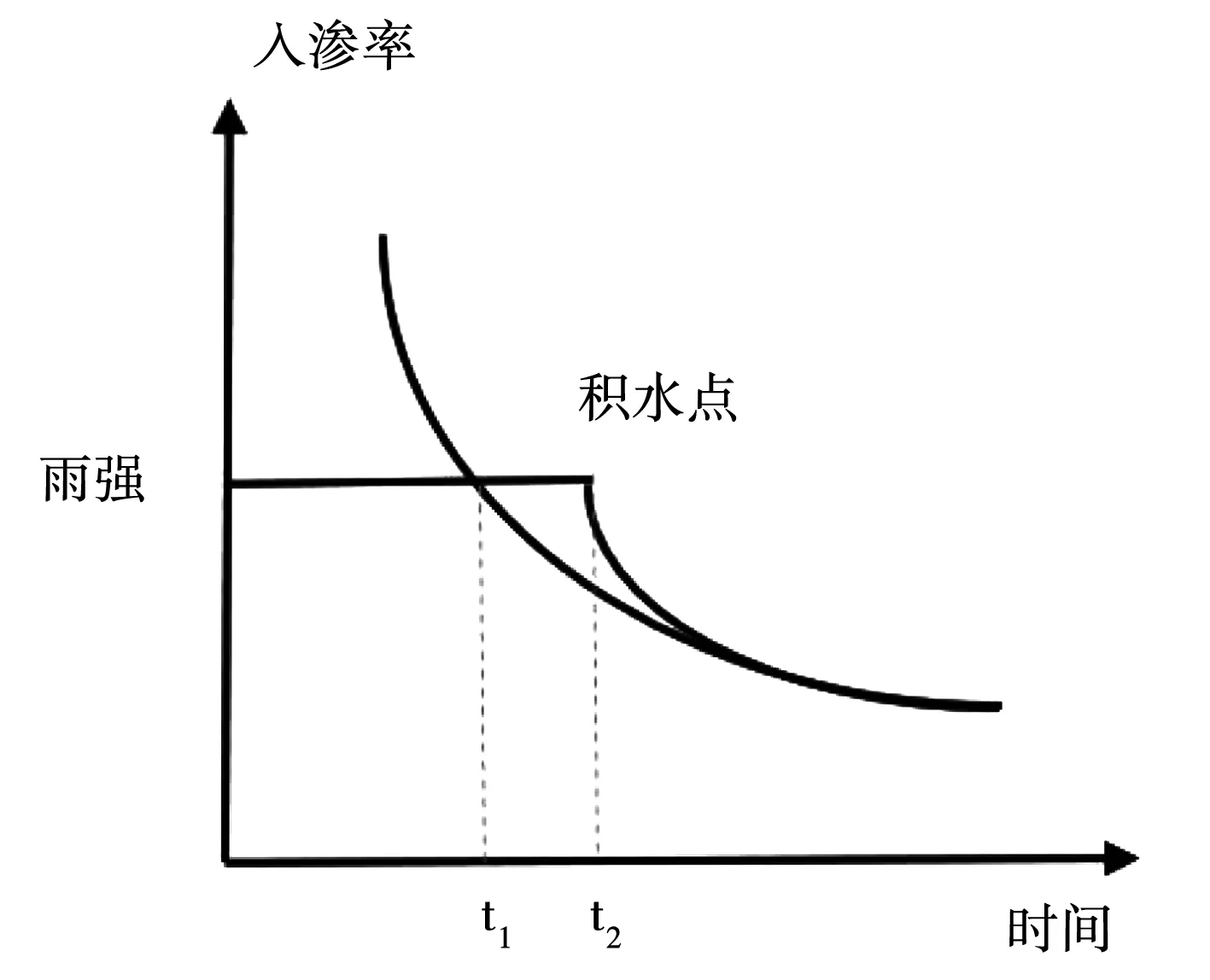
图3 实际入渗量图

入渗率与时间的关系曲线见图2。假设有某强度的均匀型降雨作用，则由图3可知，当降雨刚开始一段时间内，入渗率即为降雨强度，所有降雨全部渗入土内。这是因为初始时期土石坝表面的饱和度很低，基质吸力较大，入渗能力强。当降雨持时达到降雨强度直线与入渗率-时间曲线的交点，也即图3中的t1点时，降雨入渗率并没有马上降低，而是继续沿着降雨强度持续了一段时间，到t2才开始降低。这是因为到t1的时候，尽管达到了该时间点的最大入渗率，但是t1时间段内的总降雨量还没有达到理论的最大入渗量。而到达t2时，由于非饱和区基质吸力的降低以及浅层土体的饱和导致边坡达到积水点，入渗率开始降低，未入渗的降雨大部分转化为地表径流流走，少部分降雨从裂隙入渗或者蒸发，降雨的入渗率逐渐降低至饱和渗透系数。

基于该理论，可将降雨入渗模式分为两种：

1) 完全入渗模式：当降雨强度恒小于入渗能力时，降雨将全部入渗，不产生径流。

2) 部分产流模式：当降雨强度不恒小于入渗能力时，降雨将产生径流。

3 某土石坝渗流稳定性数值分析

3.1 工程概况

根据资料，该土石坝所在地区气候温和，雨量充沛，多年平均降雨量达到2 500 mm。土石坝为黏土心墙土石坝，坝高65 m，坝顶宽度20 m，底部坝基厚度为170 m，正常蓄水位为215 m，见图4。土石坝材料参数见表1。

图4 某心墙土石坝横截面图

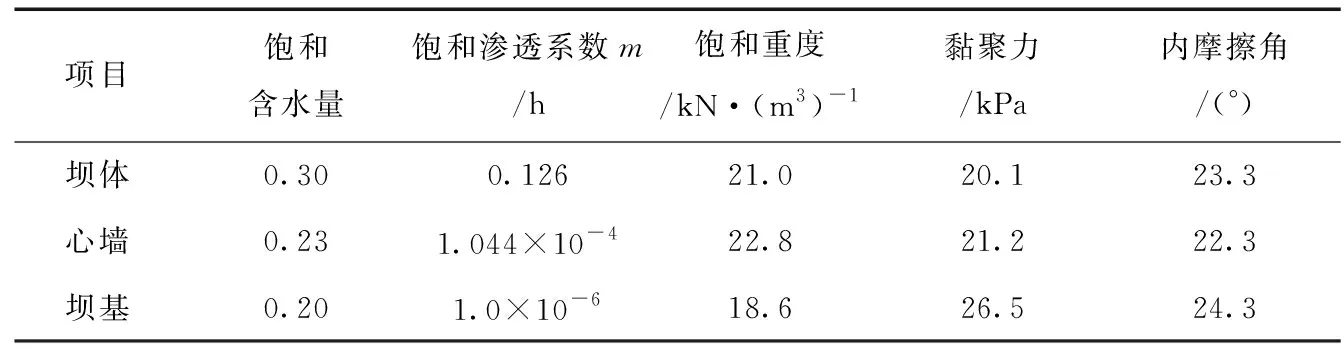
项目饱和含水量饱和渗透系数m/h饱和重度/kN·(m3)-1黏聚力/kPa内摩擦角/(°)坝体0.300.12621.020.123.3心墙0.231.044×10-422.821.222.3坝基0.201.0×10-618.626.524.3

3.2 降雨入渗作用下土石坝渗流场分析

基于土石坝所在地气候湿润多雨的特点，设定某次连续降雨雨量为480 mm，分为3种不同工况：

工况1：降雨强度20 mm/h，降雨持时24 h

工况2：降雨强度10 mm/h，降雨持时48 h

工况3：降雨强度5 mm/h，降雨持时96 h

在求解降雨入渗问题的数值软件中，Geostudio中的Seep/w是使用较为普遍的，并且它在处理入渗边界时采用迭代算法，计算结果较为可靠。因此，本文采用Seep/w程序进行降雨入渗下的土石坝渗流特性有限元计算。

对于土水特征曲线与渗透系数曲线的确定，本文采用样本函数进行估算，见图5。

计算模型依据图4建立。首先利用稳态算法计算初始渗流场，见图6，坡面初始负压接近300 kPa。

在初始渗流场的基础上，施加降雨边界条件进行3种工况下的入渗模拟试验，其渗流场计算结果见图7以及图8。从中可以看到，经过降雨作用后，非饱和区内的孔隙水压力有明显的上升趋势，非饱和区有明显的缩小趋势。对比图7(a)、图7(b)、图7(d)可知，在降雨持时一定时，降雨强度越大，孔隙水压力上升就越快，这是由于强降雨使得非饱和区的饱和度增加更快，从而导致孔隙水压力上升更快。此外，3种工况在降雨结束时的渗流场也有一定的差异。工况1的渗流场受到降雨的影响是最大的，工况3的渗流场受到降雨的影响是最小的，这是因为坝体的渗透系数比较大，因此强降雨并没有产生地表径流；另一方面，久雨(工况3)会使得坝体内的水分有更多的时间流失，孔压散去，因而工况3受到的影响是最小的。从图8可以看到，随着降雨强度的增加，非饱和区孔压随深度变化的曲线越陡，这能够说明强降雨对于高渗透性坝体的影响更为显著。

图5 各层土水特性曲线与渗透系数曲线

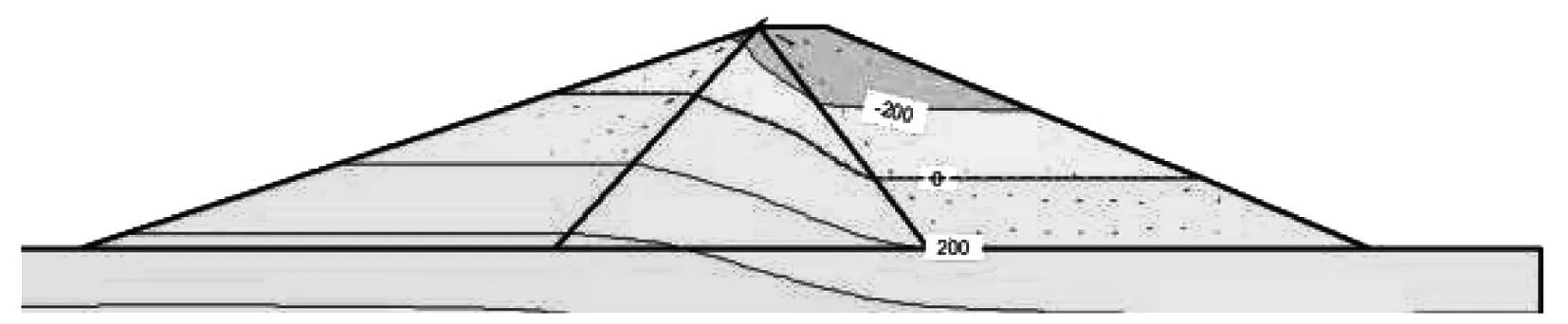
图6 初始条件下孔隙水压力分布

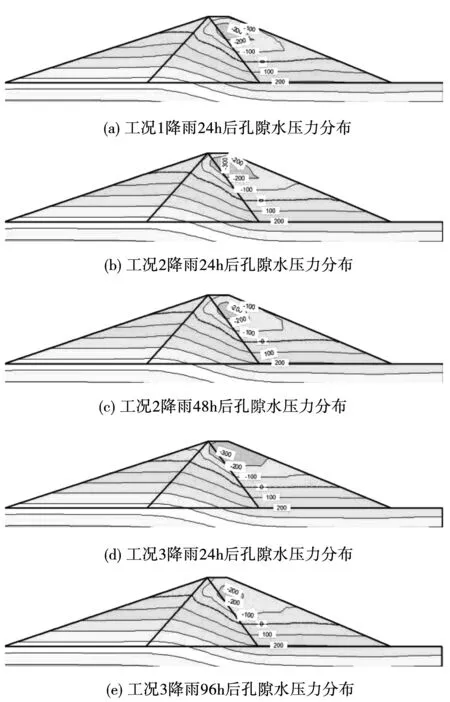
图7 各工况降雨影响后的孔隙水压力分布

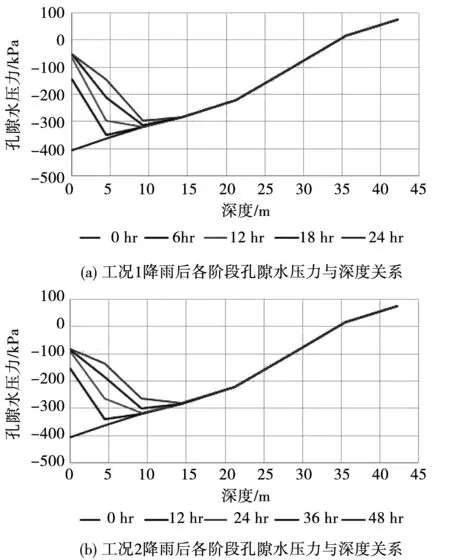
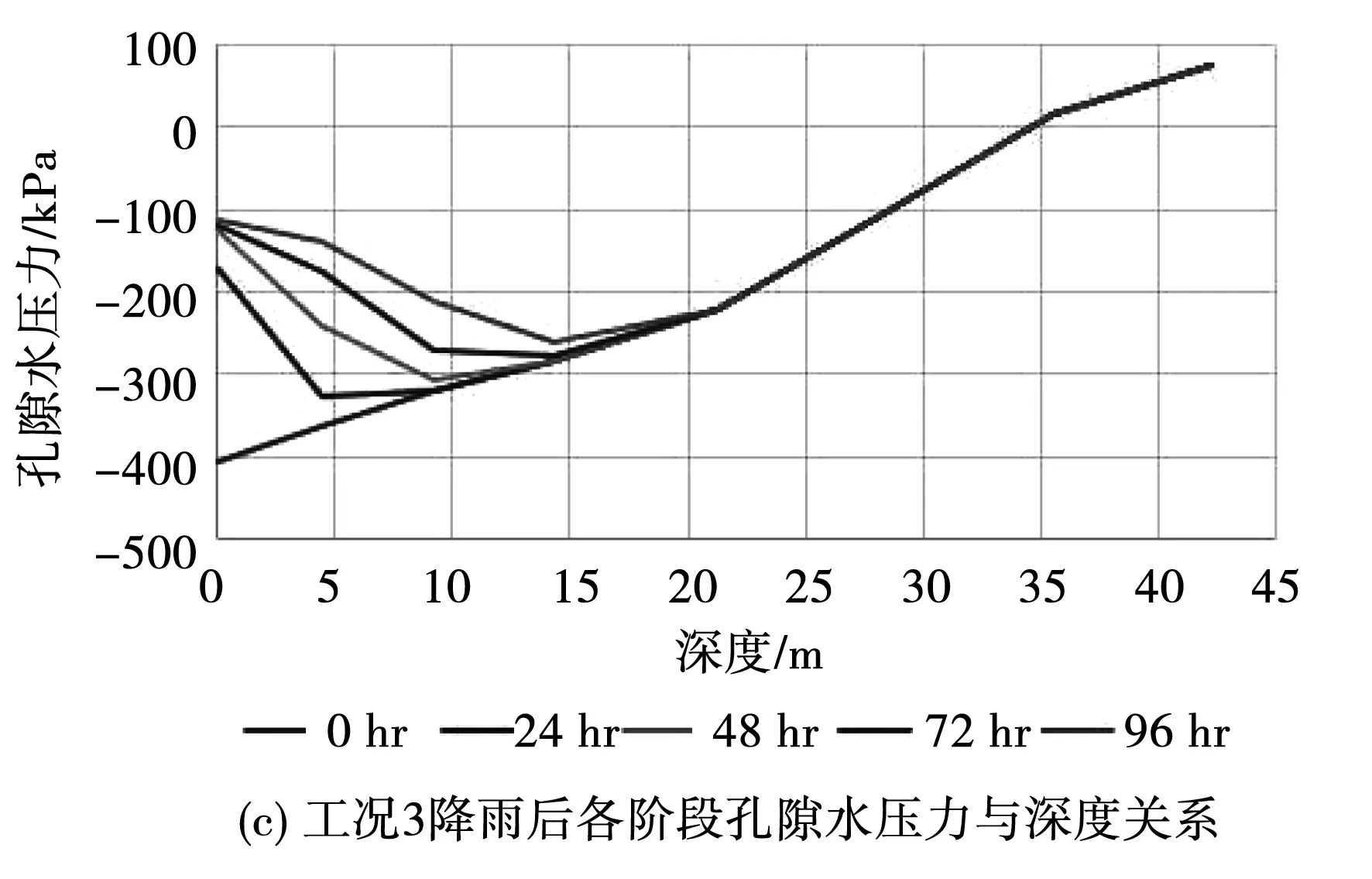
图8 各工况各阶段孔隙水压力与深度关系

3.3 降雨入渗作用下土石坝稳定性分析

土石坝的稳定性分析有极限平衡法、强度折减法等。本文使用极限平衡法中的摩根斯坦-普莱斯法，由3.2中计算得到的渗流场，基于Slope/w程序进行有限元计算，从而进行降雨入渗作用下土石坝稳定性评价。

各工况下的最危险滑面计算结果见图9。初始条件下，土石坝的安全系数为1.362，工况1降雨结束后安全系数降为1.330，工况2降雨结束后安全系数降为1.325，工况3降雨结束后安全系数降为1.325，工况1的稳定性是最低的，这与渗流场分析得到的结论相吻合。降雨后，浸润面高度也随着时间而不断上升，特别是对于久雨来说上升较为明显。这是因为久雨有更多的时间使得雨水充分入渗，抬高浸润面，同时可以看到心墙内的浸润面抬升较坝体十分微小，足见心墙起到了一定的止水作用，降低了坝体内的渗流流速，减少了渗流力对下游边坡的不利影响，增加了土石坝的整体稳定性。

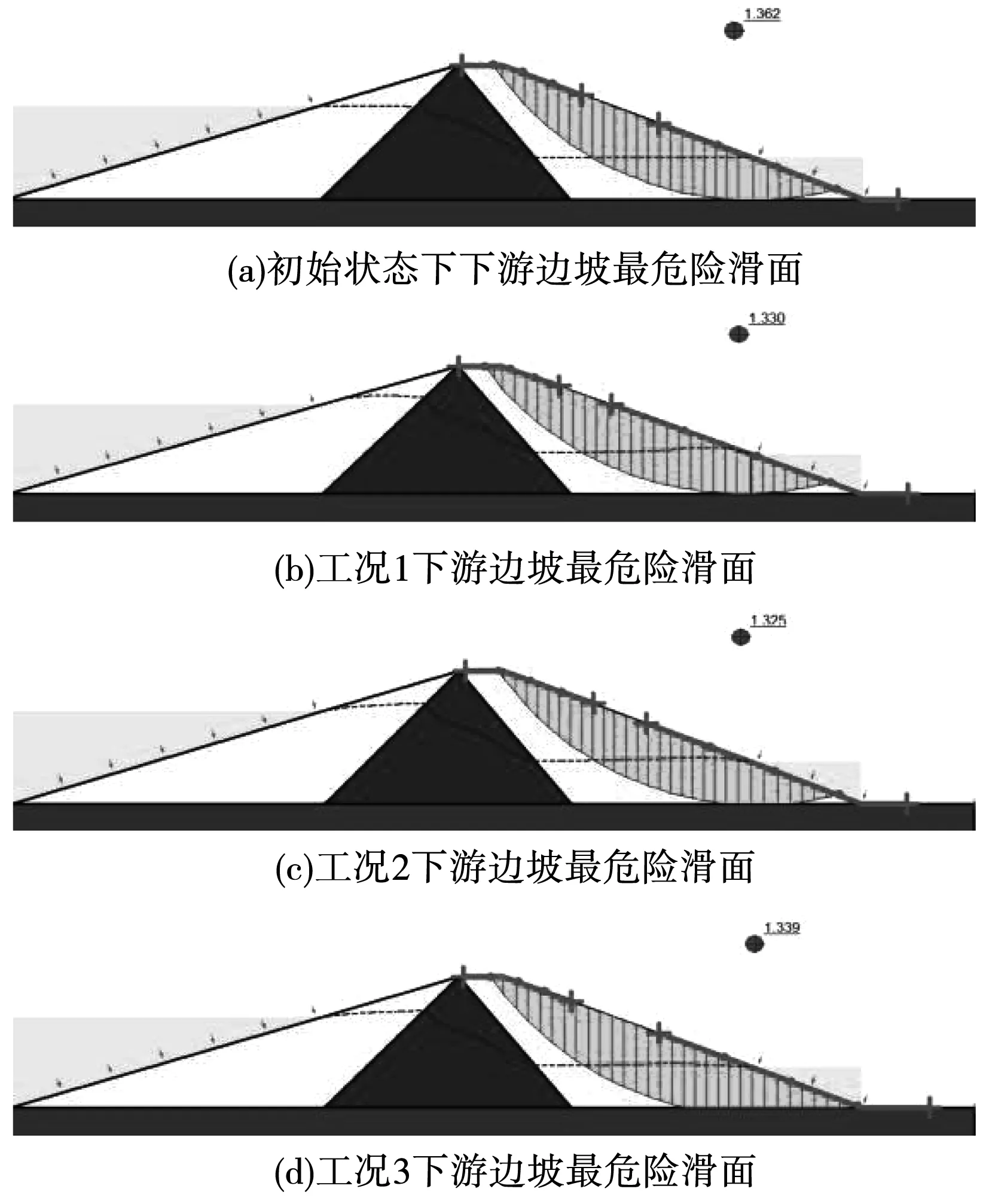
图9 各工况下下游边坡最危险滑面

4 结 论

本文基于某心墙土石坝进行降雨入渗条件下的土石坝渗流稳定性分析，运用Seep/w程序通过迭代计算得到不同降雨强度与持时的降雨下的渗流场，运用Slope/w程序通过极限平衡摩根斯坦-普莱斯法得到对应的最危险滑面以及安全系数。本文的主要结论如下：

1) 在相同的降雨持时下，降雨强度越大，非饱和区的孔隙水压力上升越快，对土石坝下游边坡更易造成不利影响。

2) 在相同降雨量下，本文所研究的心墙土石坝的渗流场受强降雨的影响更大，受降雨持时的影响较小。这是因为本文研究的坝体渗透系数较高，强降雨没有产生地表径流；另外久雨作用下，孔压有更多的时间消散，因此高渗透性的坝体受强降雨影响更为明显。

3) 心墙起到了较好的止水作用，减小了渗流力对土石坝下游坡体稳定性的不利影响。