基于双口内模控制的导引头稳定回路设计*

王业兴，骆长鑫，张 涛

（空军工程大学防空反导学院，西安 710051）

0 引言

雷达导引头稳定控制回路作为导引头跟踪和搜索模式下的内回路，为保证在弹体强扰动情况下雷达天线对目标的稳定跟踪，需要设计具有强鲁棒性的控制器来实现天线稳定平台对弹体扰动的解耦控制。同时，导弹在末制导阶段需要导引头天线实时对准目标，因此，对天线稳定回路的动态响应性能也提出了很高的要求。

在众多的控制方法中，文献[1]提出改进型干扰观测器来提高稳定平台伺服系统对扰动的抑制性能。文献[2]提出了一种基于自适应灰色预测控制的复合控制方法，实现了对复杂扰动信号的抗干扰能力。在文献[3]中，把二阶主动扰动抑制器应用到陀螺稳定平台的三回路控制模型上，取得了良好的鲁棒性和动态响应性能。内模控制的良好抗扰性、设计的简便性得到了广泛的关注，众多学者也进行了深入的研究[4-5]。文献[6]中，详细地介绍了内模控制算法在惯性稳定平台中的应用，并进一步介绍了双口内模控制改善扰动抑制比的优点。笔者在此基础上，设计了基于二次型性能指标的双口内模控制方法，实现了控制器参数在线自适应调节，仿真结果表明该方法满足了导引头稳定回路对于鲁棒性和良好动态响应的要求。

1 导引头稳定回路建模

导引头伺服系统在工作过程中分为3个模式，即预定模式、搜索模式和跟踪模式。其工作原理如图1所示。

图1中，θg表示框架角，d为弹体扰动角速率，θt表示目标位置角，θl表示光轴在惯性空间的姿态。

雷达导引头伺服系统是一个复杂的光、机、电系统，对其精确建模十分困难。本文主要针对稳定回路进行双口内模控制进行研究，同时假设框架的俯仰和方位通道不存在耦合。

电机及负载模型：电机电枢电压Ua到输出转矩Mm的传递函数为：

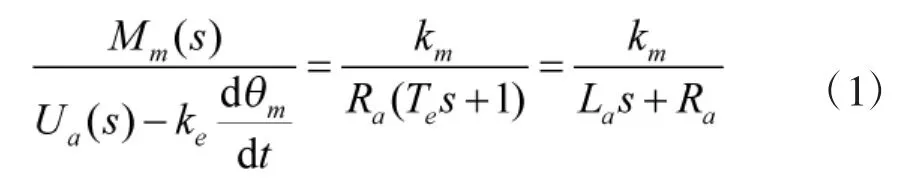
式中，ke为电机反电势系数，km为电机力矩系数，Ra为电机电枢电阻，La为电枢电感。Te=La/Ra为时间常数。

忽略电机和负载之间的非刚性因素，设J为电机及负载折合到电机轴上的总的转动惯量，则可得电枢电压到负载转动角速度ω的传递函数为：

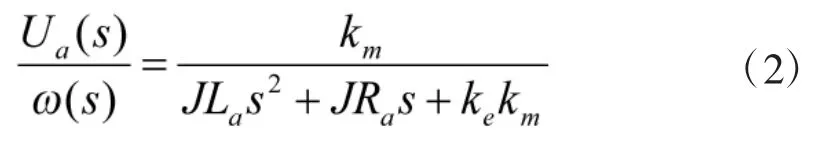
式（1）和式（2）构成了电机与平台负载模型。

速率陀螺模型：其传递函数一般可以用二阶系统近似表示：

其中，Tg=1/ωn，kg为速率陀螺增益，Tg为时间常数，ξg为陀螺阻尼系数。在导引头伺服系统中，由于速率陀螺的带宽远大于系统带宽，所以，可以将传递函数简化为比例环节：

功率放大器可看作比例环节，记为kpwm。综上，雷达导引头伺服系统稳定回路模型如图2所示[7]。

2 基于二次型性能指标的内模控制参数整定

根据图2雷达导引头伺服系统稳定回路的开环传递函数为：，即对被控对象进行数学模型时，存在建模误差。针对式（5）所示的实际被控对象，取其对象模型Gm（s）为：

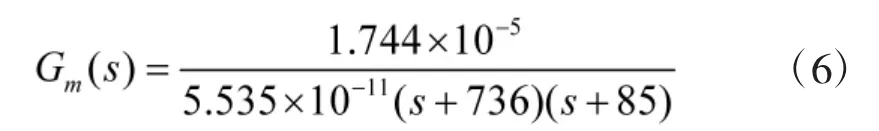
式（5）和式（6）所对应的开环对数频率特性曲线如下页图3所示。

由图3可以看出，建立的对象模型与实际模型之间存在较小的误差。下面就式（6）所对应的对象模型设计内模控制器。

根据内模控制器设计步骤，首先分析对象模型的开环零极点分布。从式（6）可以直接看出，对象模型的零极点都在s域的左半平面内，即Gm（s）是一个最小相位系统。则：

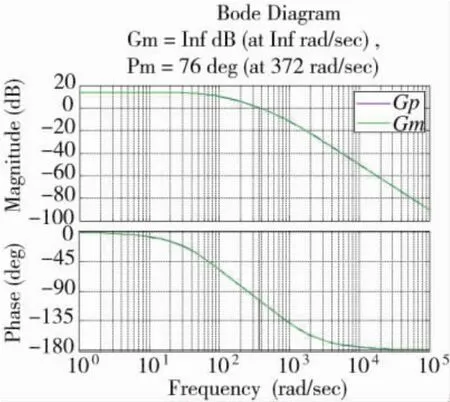
图3 实际模型及对象模型bode图

为保证内模控制器的物理可实现性，选取二阶低通滤波器[8]：

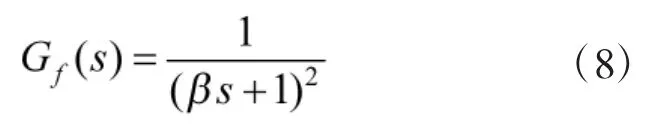
根据式（8）得到稳定回路的内模控制器为：

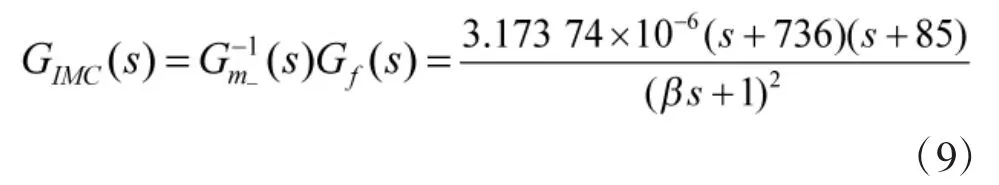
等效为反馈控制结构有：

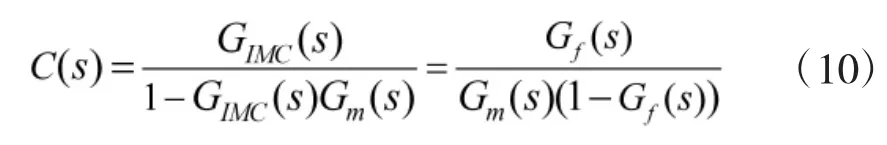
分析上式得到，设计的内模控制器只有一个可调参数β。β越大，系统的鲁棒性和抗干扰能力越强，β越小，系统的响应时间越短，超调越小。因此，β的选择应在这两方面的性能之间折中。

为进一步提高控制效果，使内模控制器参数实现在线自适应调节，设计基于二次型性能指标的内模控制器。性能指标为：

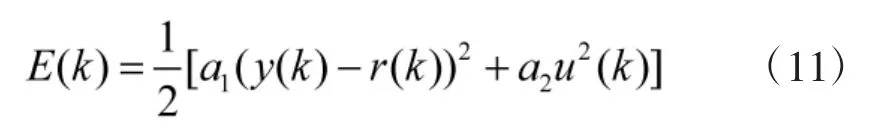
其中，y（k），r（k）分别为系统k时刻的输出和输入；u（k）为 k 时刻的控制量；a1，a2分别为误差和控制量的权重。为保证算法收敛，则必须满足：

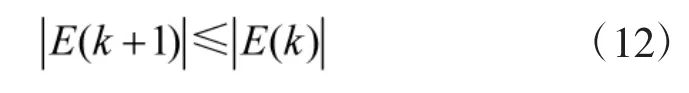
因此，结合神经网络学习规则，采用梯度下降法修正参数β，并且附加使搜索快速收敛到全局最小的惯性项，即控制算法为：

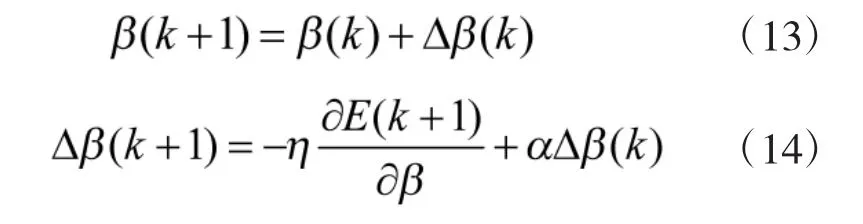
式中，α为惯性系数；η为学习速率。且

3 基于二次型性能指标的双口内模控制器设计

在传统的闭环负反馈回路的基础上添加内模回路，构成复合控制，其控制效果等效为由扰动前馈和输入前馈复合作用形成的。其结构图如图4所示[6]。

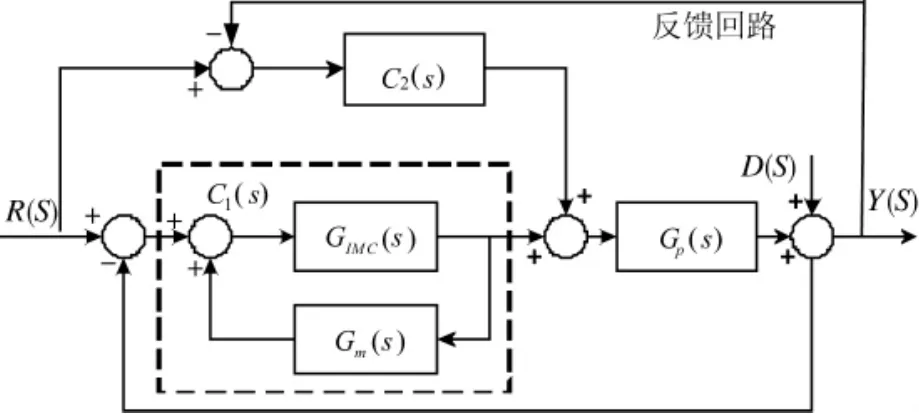
图4 双口内模控制结构

图4中，C1（s），C2（s）分别是内模控制器和反馈回路控制器。从图4可以看出，被控对象Gp（s）有两个控制输入量，因此，又被称作双口内模控制（2-port Internal Model Control，2-port IMC）。根据图4得到输入 R（s）和载体扰动 D（s）到输出 Y（s）的传递函数分别为：

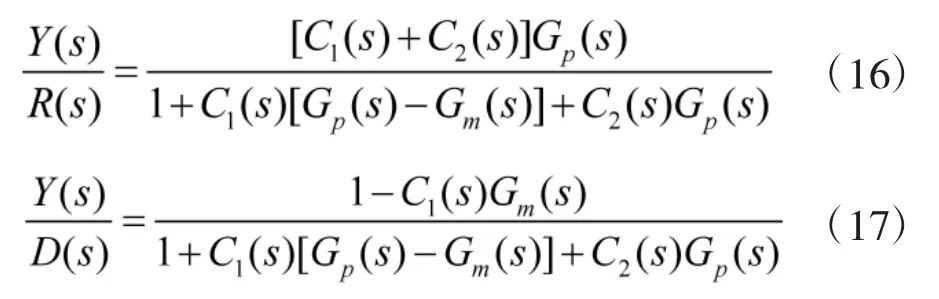
误差传递函数E（s）为：

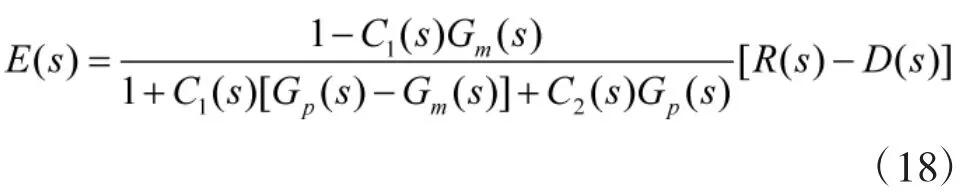
而一般结构的内模控制器误差传递函数为：

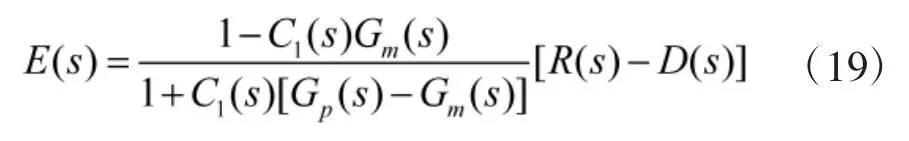
对比式（2）和式（18）知：双口内模控制结构比一般的内模控制结构在对载体扰动能力的抑制方面具有优势；对比式（25）和式（26）可知，双口内模控制的分母多了一项：C2（s）Gp（s）。当满足：

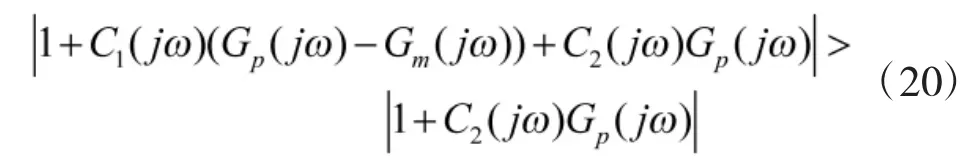
双口内模控制结构对输入的跟踪误差比一般的内模控制结构小[9]。

由式（25）得到双口内模控制系统的特征多项式为：

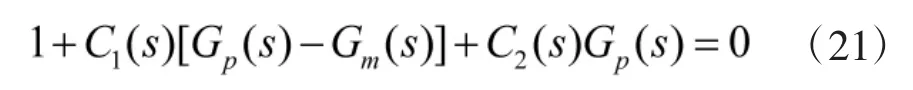
要使系统稳定，则必须使上式的根都在s域左半平面，结合式内模控制器校正后的系统闭环稳定的充要条件为[10-12]：

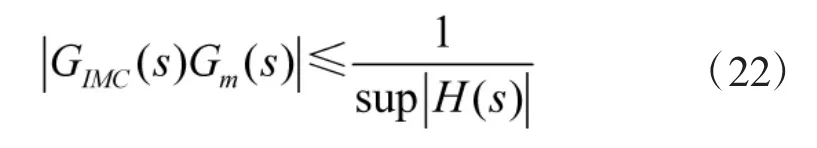
得到双口内模控制系统闭环稳定的充要条件为：

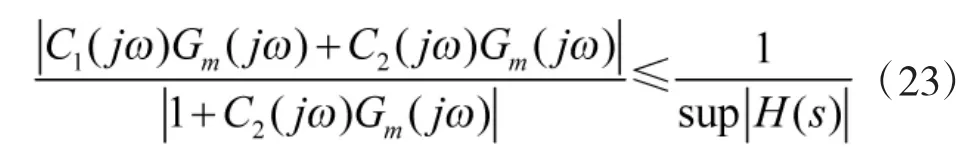
将图4所示的双口内模结构等效为经典的馈系统，其控制器为：反

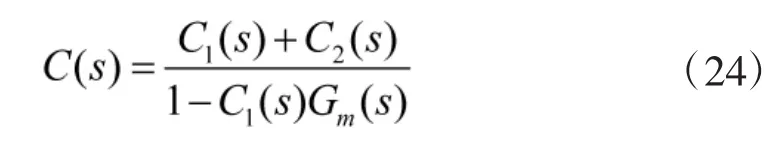
针对导引头伺服系统稳定回路，C1（s）采用上节介绍的基于二次型性能指标的内模控制器，C2（s）采用设计好的基于频域的控制器。即：

4 仿真分析

针对式（10）所示的内模控制器，选取加权系数a1=2，a2=1，惯性系数 α=1，学习速率 η=0.029 5，初值为 0.009，β 仿真步长为 0.001 s。则根据式（13）、式（14）得到参数β的自适应调节曲线如图5所示。

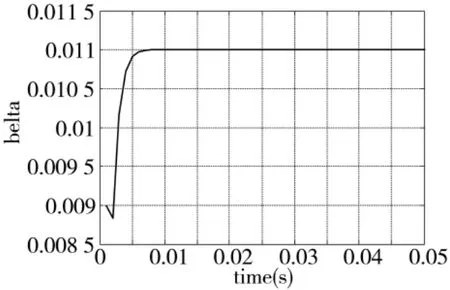
图5 β自适应变化曲线

由图5中可以看出，β迅速收敛到0.011，实现了内模控制器参数的在线调节。校正后的系统单位阶跃响应及对幅值为1°/s，频率为1 Hz的载体扰动的隔离效果分别如图6、图7所示。

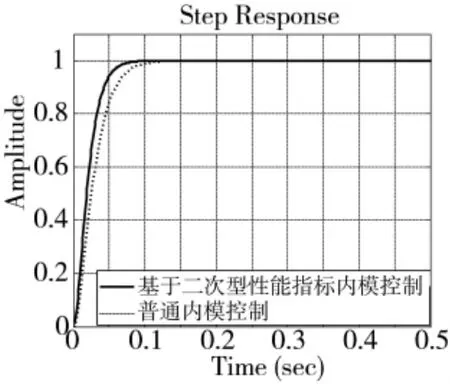
图6 校正后系统单位阶跃响应

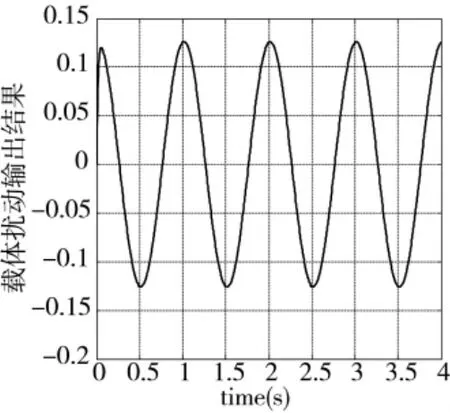
图7 校正后系统对1 Hz载体扰动的隔离效果

从图（6）可以看出，相对于普通的内模控制，基于二次型性能指标的内模控制器在调节时间上有一定的提升。但是基于二次型指标的内模控制算法对载体扰动的隔离效果不佳。

当载体扰动为0时，采用双口内模控制校正后的系统对幅值为1°/s，频率为1 Hz正弦信号的跟踪响应和跟踪误差分别如图8、图9所示。

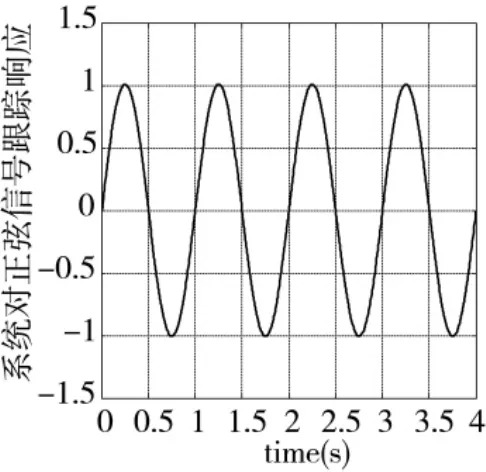
图8 1°/s，1Hz正弦跟踪响应

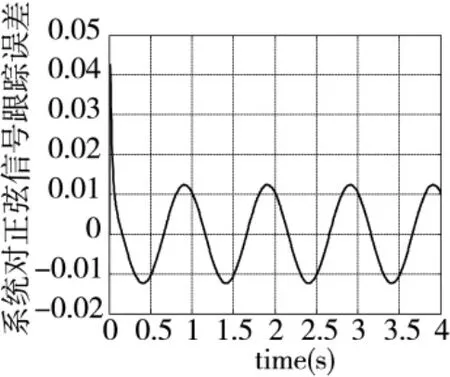
图9 1°/s，1Hz正弦跟踪误差

系统输入为0，载体扰动幅值为1°/s，频率分别为 0.5 Hz，1 Hz，2 Hz，3 Hz时，系统对载体扰动的响应如图10所示。

图10 系统输入为0时，隔离正弦扰动仿真结果

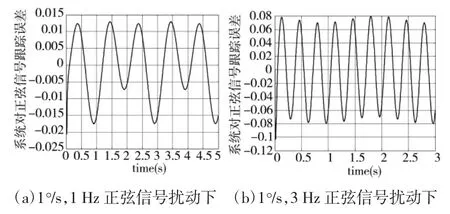
图11 系统在扰动下跟踪1°/s，0.5 Hz正弦信号的误差

当系统输入为1°/s，0.5 Hz的正弦信号时，系统在 1°/s、1 Hz和 1°/s，3 Hz正弦扰动下的跟踪误差如图12所示。

从图10可以看出，系统对0.5 Hz频率扰动信号的隔离度为-46 dB，对1 Hz频率的扰动信号的隔离度为-38.4 dB，对2 Hz频率的扰动信号的隔离度为-29.1 dB，对3 Hz频率的扰动信号的隔离度为-23.1 dB，其对载体的隔离性能满足系统对稳定回路隔离度的要求。

当系统输入为1°/s，1 Hz的正弦信号时，系统在1°/s、2 Hz和 1°/s，3 Hz正弦扰动下的跟踪误差如图12所示。

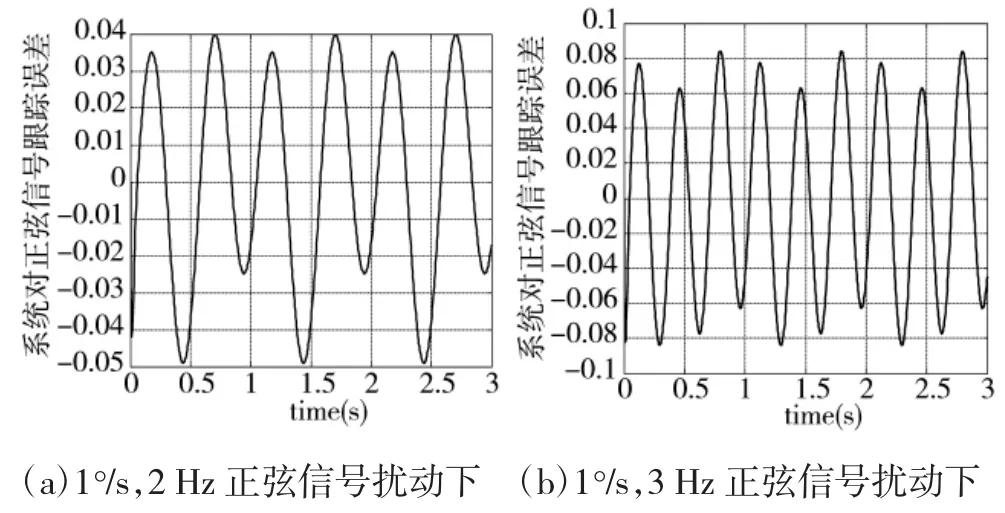
图12 系统在扰动下跟踪1°/s，0.5 Hz正弦信号的误差

从图8～图12可以看出，所设计的稳定回路控制器能够较好地跟踪输入信号，且对弹体扰动角速率有较好的隔离效果，基本满足设计要求。

5 结论

1）由于可以实现参数β的自适应调节，基于二次型性能指标的内模控制器相比于普通的内模控制，在调节时间上有一定的提升，但抗载体扰动能力较差。

2）采用基于二次型指标的控制器和频域法设计的控制器的双口内模控制在抗干扰性和系统动态性能方面由于基于二次型指标的内模控制器和普通内模控制器，达到了系统设计的指标需求。