UCAV自主空战战术机动动作建模与轨迹生成*

王 杰，丁达理，董康生，库 硕

（空军工程大学航空航天工程学院，西安 710038）

0 引言

自主制空作战代表着无人作战飞机（Unmanned Combat Aerial Vehicle，UCAV）的必然发展方向。空战行为是以机动轨迹的形式表现的，其目的就是要通过机动获取战场态势优势，因此，空战战术机动建模与轨迹生成是实现UCAV自主空战的关键技术之一。对UCAV空战复杂机动进行建模，并以此为基础建立准确、完备的空战机动动作库[1]，是实现自主空战机动轨迹规划与控制的基础。

针对机动动作建模与轨迹生成问题，文献[2]设计了一种包含描述参数的机动动作库设计方法，对不同机动动作，采用一个或多个参量进行定量描述，以体现其空间和时间特性，但并未给出控制参数的自适应调整机制，且机动动作的持续时间及参数设置合理性等问题有待于进一步研究；文献[3]提出依靠扩展操纵动作库[1]的拼接的实现复杂机动，但操纵动作库设计时往往采用极限操纵，且控制量参数设置在某一范围内不可变，难以实际应用；文献[4-5]提出以控制量变化率为优化对象，对标准机动动作进行优化，这种方式控制量变化较为灵活，但需要较多的飞行统计数据，给动作库的设计造成一定困难。

综合考虑机动动作建模的准确性和多约束条件下轨迹生成的快速性，将战术机动动作建模与轨迹生成问题分解为控制量寻优和飞行参数解算两个过程，建立了机动轨迹最优控制模型，设计了基于自适应遗传算法的求解策略，快速求解得到优化的控制量变化率，运用UCAV质点运动动力学模型对所求控制量变化率进行解算，得到机动轨迹的具体参数，并以斤斗机动为例进行了仿真验证。

1 UCAV空战机动模型结构

本文将机动动作建模与轨迹生成问题中分解为控制量寻优和飞行参数解算两个过程。UCAV机动过程可以由运动微分方程描述，其过程与实际飞行中UCAV飞行控制系统通过舵面、油门等操控飞机，在机理上完全一致。以轨迹优化模型确定控制输入量的取值来模拟飞行控制系统对飞机的操纵，而以质点运动动力学模型对控制输入量的反应解算结果来模拟UCAV对操纵指令的反应，这就是用计算机模拟UCAV机动飞行的全部[6]。其基本逻辑关系如图1所示。

2 UCAV机动轨迹运动动力学精细建模

图1 UCAV空战机动模型结构

为了准确描述机动过程中UCAV的状态特性，必须选择合适的坐标系并对空战机动轨迹进行精细建模。

本文考虑的主要坐标系包括：惯性坐标系，描述UCAV的空间位置；航迹坐标系，描述机动轨迹状态；机体坐标系，描述UCAV的姿态变化。

2.1 UCAV运动、动力学建模

考虑到模型复杂度和解算快速性的要求，建立三自由度质点运动动力学模型，模型的参数定义如图2所示。

图2 质点模型参数示意图

1）惯性坐标系下，UCAV质点运动方程

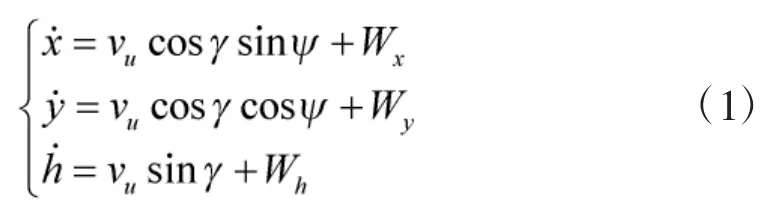
2）航迹坐标系下，UCAV质点动力学方程

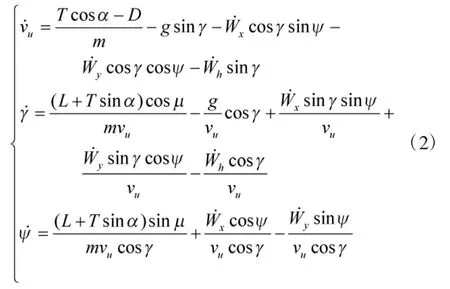
3）气动力模型

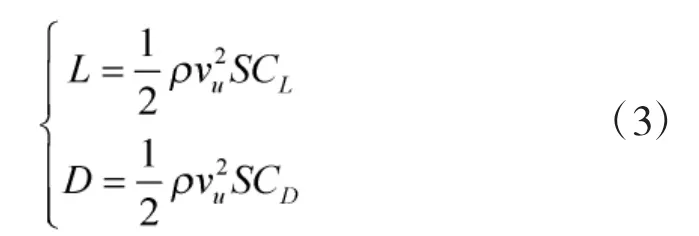
4）燃料消耗近似模型

式中，c为燃料消耗系数。

5）推力模型

考虑到发动机模型的复杂度，采用简化的推力计算模型[9]：

式中，δ为油门设置；Tmax为发动机最大推力。

2.2 UCAV机动轨迹约束建模

1）飞行包线约束。考虑UCAV实际飞行包线对复杂机动轨迹的影响，保证机动动作实施时的平台可飞行，在UCAV三自由度模型的基础上，设置约束如下[10]：

考虑UCAV飞控能力的限制，对伪控制量及其多阶导数进行约束：

考虑平台的结构安全性，同时保证平台安全返航，需满足：

式中，nz为UCAV法向过载，有；nmax为UCAV所能承受的最大法向过载，mmin为保证UCAV安全飞行的前提下最小质量。

2）状态参量约束。考虑实际飞行环境，确保安全飞行，需满足：

3 UCAV机动轨迹最优控制模型

为了提高UCAV飞行控制系统对机动动作的控制能力，减小机动动作实施过程中的状态偏差，建立以控制量变化率为优化对象的机动轨迹最优控制模型。将机动动作根据轨迹特性，划分为彼此相连的轨迹片断，每个片段有相同的控制量变化率，并将控制量变化率作为整个过程中的优化参数[4]，记为 f。

将机动动作按轨迹特性划分为彼此相连的轨迹片断，预留了较多的退出窗口，保证了机动的及时退出，符合空战实际，因而具有较强的适用性。轨迹片段的终止条件为：

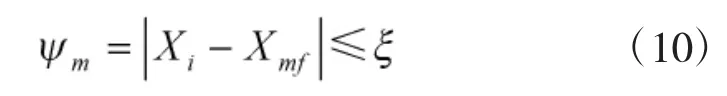
式中，Xi表示第i时刻的状态向量，Xmf表示第m个轨迹片断终止的状态向量，ξ为一个很小的数。

3.1 性能指标函数设计

3.1.1 性能指标要求

考虑性能指标函数对不同机动动作的广泛适应性，函数应主要包括以下内容：

1）关键点的状态约束。按照一定的规则设置关键点，并施加相应的状态约束，以修正动作实施过程中的状态偏差。关键点的选取可以根据统计数据获得，也可以根据需要自适应地选取。

2）控制量变化率约束。用以保证机动过程中状态参量的稳定过渡，增强系统的稳定性和安全性。

3）时间状态约束。设置时间约束，保证机动动作的快速进入和有效实施。按需划分出时间范围片段，并设置相应的状态参量范围。

4）其他约束。考虑到不同机动可能需要分别建模，预留窗口，以适应不同的机动类型。

3.1.2 性能指标函数

为了消除函数各部分之间由于量纲或数量级不同而对总体目标函数产生影响力的差距，对性能指标函数的4个部分均进行归一化处理[4]。表示形式如式（11）所示。

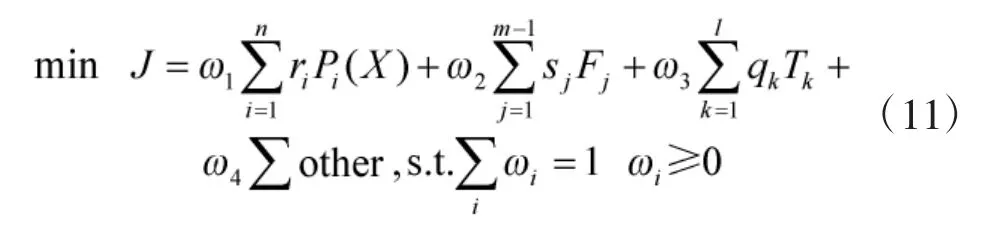
式中，n表示关键点的个数，m表示轨迹片断数，l表示时间状态片段的个数，ωi为函数各部分的权重系数。

Pi（X）表示第i个关键点超出标准约束的罚函数，定义有：

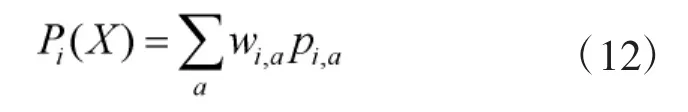
式（12）中，wi，a表示第 i个关键点第 a个参数的权重，pi，a表示第i个关键点第a个参数的罚函数；ri表示第 i个关键点的权重[4]。

Fj为相邻轨迹片段控制量变化率差值的归一化表述，有：

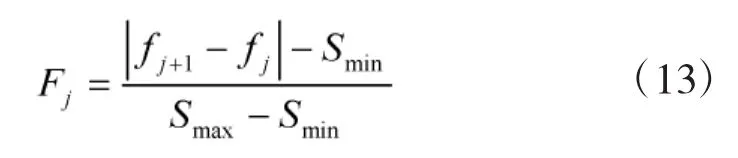
Smax和Smin分别表示控制量变化率差值的最大值与最小值；sj表示第j个变化率差值所具有权重，通常情况下，各个轨迹变化率差值的权重相同，即。

Tk表示第k个时间片段，各状态量超出标准约束的罚函数。在每个时间段内，存在多个状态点，为保证操纵的连续性，应使尽可能多地满足约束。为简化计算，设每个状态点均需要符合约束要求，定义有：

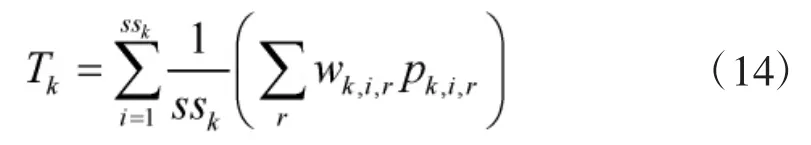
式中，ssk表示第k个时间片断的状态点的个数，有，ΔTk为该时间段的时长，Δt为仿真步长；wk，i，r和 pk，i，r分别表示第 k 个时间片段第 i个状态点第r个参数的权重和罚函数。qk表示第k个时间片段所具有的权重。

3.2 斤斗机动最优控制模型

为了验证所建模型的有效性，以斤斗机动动作为例，建立斤斗机动最优控制模型。斤斗机动是典型的铅垂面机动，主要有爬升和俯冲两个过程，具有大机动、大迎角的特点，在典型机动动作中具有很好的代表性。

以航迹倾角γ为划分对象，每10°航迹倾角划分一个轨迹片断，对于一个完整的斤斗动作，可划分为36个彼此相连的轨迹片断，每个轨迹片断均有相同的控制量变化率。假设斤斗机动过程中，航迹滚转角u=0，发动机保持最大工作状态，即油门设置δ=1，则斤斗机动过程中，优化参数为迎角变化率fα，仿真过程中，取。

3.2.1 关键点的选取

关键点对机动状态进行数学表征，保证UCAV及时修正动作偏差，但过多的关键点会造成数据冗余和计算量的增加。因此，关键点的选取，应在保证动作正常完成的同时，设置数量尽量地少。仿真以航迹倾角γ为划分对象，需要进行参数判断的关键点设置为4个，如表1所示。

表1 斤斗机动操纵关键点

对于斤斗机动过程中的4个关键点，设置状态约束及超出标准约束的罚函数。其中两个关键点的约束及对应的罚函数如表2所示。罚函数设置时，对状态参数进行了归一化处理。状态参数的阈值范围由数据统计获得。

3.2.2 时间状态约束

为了克服斤斗机动实施过程中出现的进入机动过慢，导致爬升高度过高，高点速度过低的典型错误，需要对时间状态进行约束。状态约束及其超限的罚函数如表3所示。

表2 斤斗机动关键点状态约束及其罚函数

表3 斤斗机动时间状态约束及其罚函数

3.2.3 轨迹判断终止条件

判断斤斗动作的终止状态参数为航迹倾角γ[4]，判断条件为：

式中，γj，f为轨迹片断的终止条件，ξ为一个很小的数，仿真取 ξ=0.1°。

综上，斤斗战术机动动作最优轨迹控制过程是一个多约束的最优控制问题，控制对象为第2节所建立的非线性时变系统，性能指标为4个关键点状态约束、36个控制量变化率约束和1个时间状态约束，求解对象为使式（11）所描述的性能指标函数达到最优的36组迎角变化率序列。

4 基于自适应遗传算法的求解策略

机动动作最优控制模型的求解是一个对于非线性时变系统的函数优化问题，遗传算法具有较强的适应性。本文根据遗传算法的基本原理，设计了基于自适应遗传算法[11]的最优轨迹控制问题求解策略。基本步骤如下：

第1步：确定决策变量及约束条件

选择合适的控制量，根据轨迹片断的划分方式，分别确定其变化率序列长度及取值区间。

第2步：建立优化模型

根据机动动作状态约束，确定性能指标函数J的类型及数学表示形式，如式（11）所示。

第3步：确定编码方式

采用十进制编码方式，对染色体进行编码，将控制量变化率序列对应染色体上的基因片段。对于斤斗机动，每一个染色体对应一个由36个迎角变化率构成的序列。

第4步：确定个体评价方法

如式（11）所示，性能指标函数非负，优化目标是求函数的最小值。遗传算法以个体适应度的大小来确定该个体被遗传到下一代群体中的概率，个体适应度值越大，其被选择的概率就越大，因此，遗传算法适合求解适应度函数的最大值。故将性能指标函数的倒数作为适应度函数，定义为：

f为个体适应度函数，J为性能指标函数。适应度函数的计算流程如图3所示。

第5步：设计遗传算子

选择运算采用顺序选择策略。首先按适应值大小对个体进行排序，适应度值最大的个体选择概率为q，排序后的第j个个体选择概率为：，NP为种群数量。保证每个个体都能够被选中产生后代，保持种群的多样性。

交叉与变异运算采用自适应策略[12]，使交叉概率和变异概率能够随适应度值大小自动改变，当种群各个体适应度趋于一致或趋于局部最优时，交叉概率和变异概率二者同时增加，而当种群适应度比较分散时，两者均自适应减小。交叉运算使用单点交叉算子，变异运算采用基本位变异算子，交叉概率Pc和变异概率Pm计算方式如下

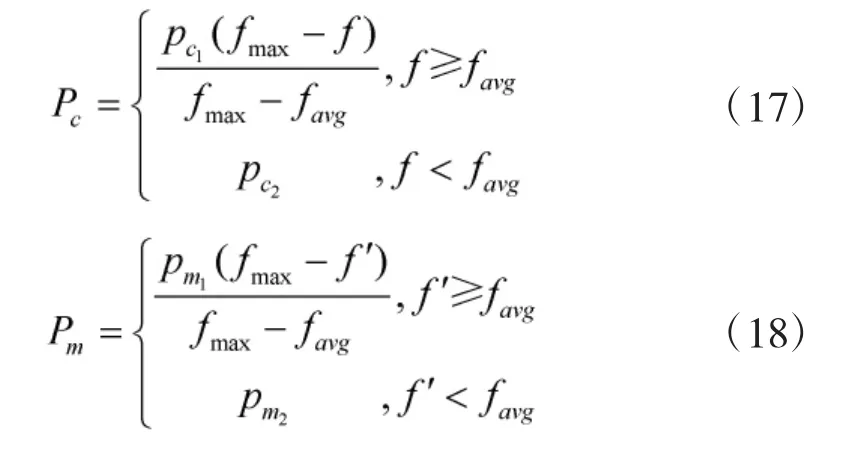
其中，fmax为种群中的最大适应度值；favg为群体平均适应度值；f为要交叉的个体中较大的适应度值；f′为要变异的个体的适应度值，为杂交常数，为变异常数。

第6步：设定遗传算法的运行参数

根据实际需要确定染色体编码长度L，种群大小NP，进化代数NG，选择概率q，杂交常数，变异常数。

图3 适应度函数计算流程

5 模型验算与仿真分析

以斤斗动作为例，对UCAV战术机动模型进行验证。

5.1 参数设置

仿真实验中，忽略风场扰动的影响，UCAV初始方位设置为（0，0，1 000）km，初始速度 vu0=220 m/s，迎角 α=0°，航迹倾角 γ=0°，航迹偏角 ψ=0°，航迹滚转角 μ=0°；油门设置 δ=1；仿真步长 h=0.1 s；UCAV性能参数参照文献[6]。性能指标函数各部分权重之比为，即优先保证系统的稳定性；关键点的权重之比为，即尽可能地满足机动改出条件；关键点各状态参量的权重相同。

遗传算法的性能参数设置如下：种群数量NP=500，进化代数NG=1 000，染色体编码长度L=36，杂交常数，变异常数。

5.2 仿真曲线与结果分析

适应度函数进化的曲线如图4所示。由图4可知，种群均值和最优适应度函数值随进化代数迅速增加，至159代时趋于平稳，第840代时，收敛到全局最优，最优控制量变化率曲线如图5所示。

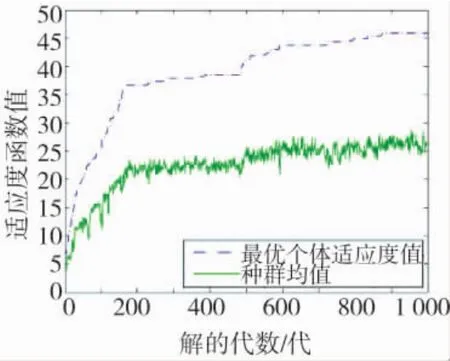
图4 适应度函数进化曲线

图5 迎角变化率曲线

图6 迎角随航迹倾角变化曲线

参照所建立的UCAV空战机动模型结构，将所求得的最优控制量变化率序列带入质点运动动力学模型进行飞行参数解算，得到状态变量[x，y，h，v，γ，ψ，m]T的具体值。

控制量迎角随航迹倾角的变化曲线如图6所示。综合图5和图6可知，斤斗机动迎角变化过程分为两个阶段，第1个阶段0°≤γ≤250°，迎角随航迹倾角逐渐增大，至γ=250°，迎角达到最大值；第2阶段250°＜γ≤360°，迎角随航迹倾角增大逐渐减小，直至满足终端约束要求，斤斗动作正常改出。

航迹变化曲线如图7所示，UCAV姿态角度由式（7）求得。机动过程中，铅垂方向，最大高度差值为1 851 m；水平方向，最大水平跨度为1 987 m。

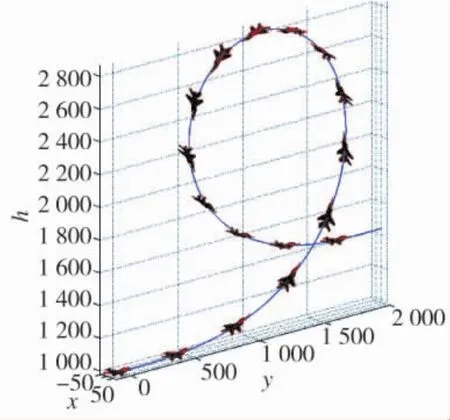
图7 航迹变化曲线

图8和图9分别表示过载随时间和航迹倾角的变化曲线。过载产生主要受升力L、推力T和迎角α的影响，参照气动力变化曲线（如下页图10）及过载转化公式，可知升力L对法相过载的产生起着决定性作用。机动过程中，法向过载变化过程可分为4个阶段，大致与升力变化曲线保持一致，当γ=40.71°，仿真时间t=6.1 s时，法向过载取最大值，为nz=5.29。仿真飞行时间为33.5 s。仿真过程中，速度随航迹倾角的变化曲线如下页图11所示，可见，机动实施时，先短暂加速，以完成进入机动前的准备，之后进行减速爬升和加速俯冲两个过程，这与飞行实际是相吻合的。

图8 法向过载随时间的变化曲线

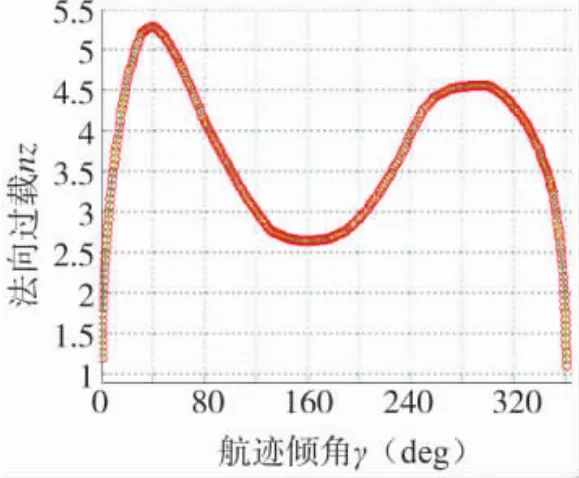
图9 法向过载随航迹倾角的变化曲线

综上可知，所建模型，能够准确描述和表征机动动作；求解策略能够迅速收敛到全局最优，并得到控制量变化率；生成的轨迹符合机动动作的几何形态和状态特性，并满足时间窗口限制。

图10 气动力随航迹倾角的变化曲线

图11 速度随航迹倾角的变化曲线

6 结论

本文面向UCAV自主空战技术的迫切需求，对UCAV战术机动动作建模与轨迹生成问题进行了研究，提出了实现UCAV空战机动动作的模型结构，建立了精细的UCAV质点运动模型，设计了以控制量变化率为优化对象的机动轨迹最优控制模型，并给出了基于自适应遗传算法的求解策略，仿真表明所建立的模型可以较好地体现机动动作的几何形态和状态特性。研究成果对UCAV空战战术决策、空战战法模拟、以及飞行员辅助驾驶等问题具有广泛的适用性。