基于代理模型的空间飞越发射窗口
2019-01-14向开恒李人杰陈杨
向开恒 李人杰, 陈杨
(1. 航天科工空间工程发展有限公司, 北京 100854; 2. 北京电子工程总体研究所, 北京 100854)
空间飞越是指运行在停泊轨道的航天器,收到指令后沿着设计的转移轨道,从距离目标航天器或天体极近的空间一点(飞越点)掠过,进行短时间观测并远离的过程[1]。对空间飞越的研究具有重要意义。首先,飞越探测是深空探测的一种重要方式,如嫦娥二号对4179 Toutatis小行星的飞越探测[2]。其次,在进行在轨服务之前,对目标实施飞越可以对其进行快速有效的观察,获取目标运行状况、故障类别等信息[3]。最后,飞越式接近还可以作为一种安全接近方法,使在轨服务航天器沿一条无碰撞路径到达目标,且保证出现故障时也能安全撤离[4-5]。
飞越轨道的优化设计是实施空间飞越的基础,然而因为各种不确定性因素的存在,航天器难以按照预先设计的最优轨道进行飞越,所以相对于轨道优化设计,更为关注的是在一定初始条件下发射窗口的计算方法。目前对运载火箭的发射窗口计算已较为成熟,但是对从停泊轨道出发的发射窗口研究较少。文献[6]使用遍历搜索方法,研究了嫦娥二号从环日地L2点轨道出发,飞越探测小行星的发射窗口;文献[7]提出了基于发射窗口的天基发射方案,在给定初始条件下计算了发射窗口,研究了轨道规划策略。在进行分析计算时,不同初始条件下的发射窗口不同,初始条件是一个重要的影响因素,所以有必要对此进行研究。
为研究初始条件的影响,需要对若干组不同初始条件下的发射窗口进行分析,而每一组都需要采用数值方法进行遍历搜索来计算,因此计算量大、耗时长,需要研究高效的计算方法。代理模型(surrogate models)技术是一种降低计算成本的有效方法,所谓代理模型是指计算量小、但计算结果与真实模型的结果相近似的分析模型。在研究过程中用代理模型替代真实的高精度模型,可以有效地减少计算量、提高仿真计算的效率[8-9]。代理模型技术是多学科优化领域的重要研究内容之一,但在航天器轨道设计与发射窗口计算中的应用较少。文献[10]通过构建BP神经网络(Back Propagation Neural Network,BPNN)代理模型,进行了空间飞行器可遭遇区与最小速度增量遭遇点的计算。
本文针对空间飞越问题,研究不同初始条件下发射窗口的数值计算方法和代理模型技术,对比分析不同的代理模型构造方法在解决该问题中的效果和适用性,基于代理模型快速分析初始条件对发射窗口的影响。
1 考虑初始条件的发射窗口计算
1.1 空间飞越任务流程
一次空间飞越任务如图1所示。
都市生态的内涵十分丰富,除了自然生态之外,还涉及到了都市的人文生态,因此都市生态不仅关系着城市居民的生活环境质量,同时也影响着其精神层面的发展[1]。通常情况下,我们会将都市生态分为两个部分,其中自然生态即是指城市环境,人文生态则是指一些历史遗留的古建筑和非物质文化遗产。当前阶段的市政工程管理存在明显的片面性,普遍存在重视自然生态保护,忽视人文生态保护的情况,对文化遗产的继承发展造成了严重的阻碍。
从接收飞越任务指令到完成飞越任务的具体流程如下:
Cloumn-Bot采用Arduino mega 2560单片机作为核心控制器,其上具有54路数字输入输出,适合需要大量IO接口的设计.
1)t0时刻接收指令,此时飞越航天器和目标航天器的位置分别为rf0、rt0。
图4是美国前三轮加息周期中上证指数的月线波浪形态。通过观察不难看出,美国加息时段中的A股存在一个共性之处,即大致都呈现出先跌后涨的V形走势,并与中国股市特有的浪形态势相契合。自2015年12月以来的美联储这轮加息周期时间最长,共已加息9次。2016年1月至今三年时间里,A股主要经历了前两年的缓慢上扬和今年的持续大幅调整。有预期认为2019年美国还将加息两次,那么,中国A股是否会在新的一年里止跌并出现一波上涨呢?目前看来的确有这样的可能。关于近几年A股市场走势的浪形分析,读者朋友可参考上期专栏文章及图示。
3) 在t1时刻,飞越航天器施加脉冲进行变轨。
4) 飞越航天器变轨后,飞行Δt时间,到达t2时刻,t2=t1+Δt。此时飞越航天器到达飞越点,实现飞越。因为飞越点与目标航天器的距离和该点与地心的距离相比极小,可以忽略,所以假定此时飞越航天器和目标航天器的位置均为rt。
相似度比较计算是信息分类及判别的关键技术。由于自然语句是由字、词语及关键字等组成,相似度的比较计算可以分为词语相似度、语义相似度、句子相似度、句长相似度等多个特征方面。其中,词语相似度是指两个或几个词语所表达的内涵相同或相近,可以互相替换使用而不改变整个语句的文义的程度,常用的词语相似度算法有基于统计和基于规则的两种方法;句子相似度主要由基于语法的分析和基于词汇相似度矩阵的分析方法。通过多个特征相似度的分析计算,对语句及其含义进行综合对比研究,从而达到自动评阅的目的。
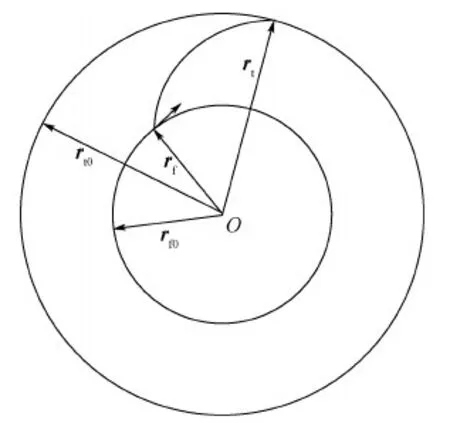
图1 空间飞越任务示意图Fig.1 Schematic diagram of space fly-by mission
完整的飞越任务时序如图2所示。定义从接收指令到施加脉冲前的时间Δt0为等待时间,从施加脉冲到完成飞越的时间Δt为转移时间,总时间为飞越时间Δts= Δt0+Δt。
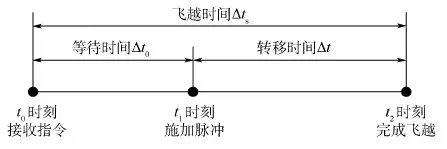
图2 空间飞越任务时序Fig.2 Timing sequence of space fly-by mission
1.2 不同初始条件下发射窗口计算方法
学校里教什么行业的班级都有:厨师(刀功、面案、烹饪、摆台),汽车修理和驾驶,公共电汽车售票员,园艺工(花匠),开城市洒水车,美容美发,电影放映员,澡堂子服务员,商店售货员,服装裁剪,仓库保管员,会计、出纳和文秘,差不多就是一个综合性社会服务业预备班。
2.2 NAFLD组与对照组CD4+CD25+T细胞结果比较 NAFLD患者外周血CD4+CD25+T细胞百分率较对照组明显降低,差异有统计学意义(P<0.05),见表2。
将所有满足约束的t1时刻的集合作为发射窗口,发射窗口随t0时刻初始条件的变化而变化。假设不考虑摄动力的影响,飞越航天器和目标航天器的轨道在空间固定不变,则t0时刻两者的初始位置rf0和rt0只与其平近点角mf0和mt0有关。所以,研究初始条件对发射窗口的影响即研究平近点角的影响,具体步骤如下:
步骤1初始化飞越航天器平近点角mf0=0°。
Put the optimized formula of glass holder profile into SAP system, and extend BOM list code[5-7]. The length of each profile can be calculated for actual need. The result can be listed in related order as below:
步骤2初始化目标航天器平近点角mt0=0°。
清朝沿袭明朝的闭关锁国政策,直到1684年之前都禁止海外贸易。1684年,清政府设广州、漳州、宁波、云台山(今江苏镇江)四处为对外通商口岸,并引用已有的内陆口岸的规定管理海关。1757年(乾隆二十三年),清政府撤销其他口岸,限定广州一口通商,直到鸦片战争,一直实行单口贸易政策。关税税率大体为进口税率是16%,出口税率4%④。进出口关税税率的差异一定程度上体现了清政府鼓励出口、抑制进口的初衷。但由于进出口规模有限、海关行政效率低下及贪污腐败盛行,关税对整个财政收入的贡献微乎其微。
步骤4初始化转移时间Δt=Δtmin,Δtmin为最小转移时间。
步骤5根据mf0和mt0计算飞越航天器和目标航天器的初始位置rf0、rt0,然后根据Δt0和Δt计算出rf、rt,使用普适变量法求解Lambert问题得到速度增量Δv;计算飞越时间Δts=Δt0+Δt;如果Δv<Δvmax且Δts<Δtsmax,则t1时刻属于初始条件为mf0和mt0时的发射窗口,其中Δvmax和Δtsmax分别为变轨速度增量和飞越时间的最大允许值。
因为本文研究的是空间飞越而非空间交会,所以飞越点速度约束暂不考虑;本文采用二体动力学模型下的Lambert变轨,不考虑摄动因素,因而可以保证飞越点位置约束满足要求,且无需考虑中途修正及其燃料约束;在飞越点附近对目标航天器进行观测时要求日光、月光、地气光等不能进入观测设备的视场影响观测效果,仿真结果表明,光照条件在短时间内变化极小,因此本文假设在任务期间飞越点光照条件不变且满足约束。而变轨速度增量和飞越时间是最重要、最基本的2个约束,如文献[7,10-11]均在只考虑这2个约束的条件下来计算发射窗口。综上,本文重点考虑变轨速度增量约束和飞越时间约束。
步骤3初始化等待时间Δt0=Δt0 min,Δt0min为最小等待时间。
步骤6更新Δt=Δt+Δtstep,Δtstep为转移时间的步长;如果Δt<Δtmax,则返回步骤5,否则进行步骤7,其中Δtmax为最大转移时间。
(一)多阅读积累故事。每天在课每周我会用一节课时间,给同学们讲故事,有时是我站在讲台上给同学们绘声绘色手舞足蹈的边说边演;有时我把故事说完,会让孩子根据故事中的角色进行表演,并且允许他们自行改编。这也为他们改变故事和给故事写续集做好了充分的准备。
步骤7更新Δt0=Δt0+Δt0step,Δt0step为等待时间的步长;如果Δt0<Δt0max,则返回步骤4,否则进行步骤8,其中Δt0max为最大等待时间。
步骤8更新mt0=mt0+mtstep,mtstep为目标航天器平近点角的步长;如果mt0<360°,则返回步骤3,否则进行步骤9。
步骤9更新mf0=mf0+mfstep,mfstep为飞越航天器平近点角的步长;如果mf0<360°,则返回步骤2,否则结束。
计算过程如图3所示。
可以看出,研究初始条件对发射窗口的影响,需要对mf0、mt0、Δt0和Δt4个变量进行循环计算,计算量极大。
文献[11]研究了一种特殊的情况:飞越航天器和目标航天器的轨道为共面圆轨道时,初始条件对发射窗口的影响。定义初始相位角θ0为t0时刻飞越航天器与目标航天器的地心角,即两者纬度幅角之差,则在共面圆轨道的假设下,初始条件的变化只与初始相位角θ0的变化有关。因此,只需研究初始相位角的变化对发射窗口的影响,即在计算过程中只需θ0、Δt0和Δt3个变量的循环。研究结果显示,在共面圆轨道情况下计算耗时约为10 min。而对于一般情况,初始条件与平近点角mf0和mt0有关,相比于共面圆轨道,计算过程多了一重循环,假设以1°为步长,则计算量为原来的360倍,预计耗时约60 h,计算时间过长,因此需要研究提高计算效率的方法。
1.阔盘吸虫病。阔盘吸虫病感染的环境需要含虫卵粪便、蜗牛及牧草混合在一起,我国南方牛、羊受感染的季节主要在秋季(7~10月)。其它季节发病率不高。
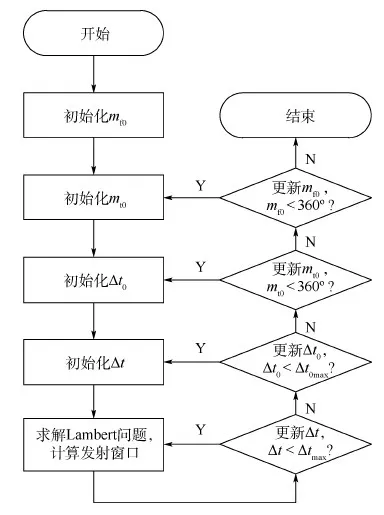
图3 发射窗口计算过程Fig.3 Calculation process of launch window
2 代理模型技术
代理模型是根据真实模型的输入/输出样本数据来构造的一个替代模型。构造代理模型一般需要3个步骤:首先,选取样本点,通过真实模型计算出对应的输出值,生成输入/输出样本数据;然后,根据样本数据构造出代理模型;最后,对代理模型的精度进行校验,评估其可信度[12-13]。
2.1 生成样本数据
构建代理模型,首先是选取样本点并计算样本点的输出值。通常使用试验设计作为采样策略,通过科学合理的数学安排,在设计空间内生成能够反映真实计算模型的数值特征的样本点[14]。常用的试验设计方法包括:全析因设计、正交设计、中心复合设计、均匀设计、拉丁超立方设计等。
在试验设计中,输入变量被称为因素,因素所处的状态称为水平[15]。本文选用全析因设计方法,该方法将所有因素的所有水平进行组合来选取样本点,能够全面反映输入变量及其相互间的交互作用对输出值的影响。全析因设计生成的样本点数ns为
ns=(nl)nv
(1)
式中:nv为因素数,即输入变量的个数;nl为水平数。
通过试验设计得出样本点x=[x1,x2, …,xns]之后,需要计算每个样本点所对应的输出值,针对本文研究的问题来说,即为样本点所对应的发射窗口长度。发射窗口长度的计算使用1.2节的方法,只是对于每个样本点来说,mf0和mt0确定,只需计算Δt0和Δt2个变量的循环,即步骤3~步骤7。最终得到样本点输出数据y=[y1,y2,…,yns]。
生成输入/输出样本数据后,可以进行代理模型的构造。
2.2 构造代理模型
常用的代理模型构造方法包括多项式响应面法(Response Surface Method,RSM)、移动最小二乘(Moving Least Square,MLS)、径向基函数(Radial Basis Function,RBF)、Kriging模型、BPNN和支持向量回归(Support Vector Regression,SVR)等。文献[14]从近似精度、计算成本、实现难度等方面对典型的代理模型构造方法进行了对比评估,得出RBF模型和Kriging模型的综合性能优于其他代理模型。因此,本文研究这2种代理模型在空间飞越发射窗口计算中的应用。
设计导入期的目的,一是稳定基线,二是洗脱药物。14项研究中有6项(42.86%)设计了导入期,时长1~4周。其中1周1项,2周2项,4周3项。随访目的为观察腹痛的复发率。14项研究中10项设计了4周~6个月随访。其中,4周5项(35.71%),8周3项(21.43%),12周及6月各1项(各占7.14%)。
μ=(dTQ-1d)-1dTQ-1y
径向函数是以未知点与样本点之间的欧氏距离为自变量的一类函数。以径向函数为基函数,通过线性叠加构造出来的模型即为RBF模型,其基本形式为[14,16]
(2)
式中:fR(xu)为未知设计点xu处RBF模型的预测值;α=[α1,α2,…,αns]T为权重系数向量;gi(xu)为径向函数,常用的径向函数有
(3)
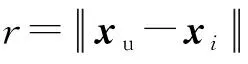
构建RBF模型的重点是求解权重系数α,α应满足插值条件,使样本点处的预测值与真实值相等,即
(4)
式中:xj为第j个样本点;yj为第j个样本点的输出。式(4)的矩阵形式为
Gα=y
(5)
式中:G为径向函数矩阵
(6)
则权重系数
α=G-1y
(7)
2.2.2 Kriging模型
Kriging模型是由南非地质学者Krige提出的一种针对空间分布数据的无偏最优估计插值模型,由全局模型和局部偏差模型叠加而成,其基本形式为[14,17]
fK(xu)=w(xu)+Z(xu)
(8)
式中:w(xu)为多项式全局近似模型,反映近似对象在设计空间内的总体变化趋势,可取常数μ;局部偏差项Z(xu)是一个随机过程,其均值为零、方差为σ2、协方差非零。Kriging模型的近似能力主要由局部偏差项Z(xu)决定,其协方差矩阵可表示为
Cov[Z(xi),Z(xj)]=σ2Q[q(xi,xj)]
(9)
式中:Q为对称相关矩阵;q(xi,xj)为高斯相关函数
(10)
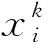
对任一设计点xu,引入相关向量p(xu)为
fK(xu)=μ+pT(xu)Q-1(y-dμ)
(11)
由此,Kriging模型可以表示为
我的母校已不复存在了,连身后那幢曾与我们朝夕相伴的水房也龟裂了,坍塌了。在那些山墙下的垃圾与瓦砾堆中,蹿出的紫棒花和野草正叙说着不尽的孤寂。秋风中那一排粗大的杨树,正不断地往下飘落着桔红色的叶子。羁旅行役,半世蹉跎,这一生我已经走完了大半了呵……
p(xu)=[q(xu,x1),q(xu,x2),…,q(xu,xns)]T
(12)
式中:d可设为元素全为1的ns维列向量。模型中存在3个未知量:μ、θ和σ2,其中μ和σ2都是θ的函数,两者的最小二乘估计可通过式(13)和式(14)求出:
2.2.1 RBF模型
(13)
(14)
将μ和σ2的表达式代入式(15)所示的一维优化问题可求解得到相关参数:
s.t.0≤θ≤∞
(15)
2.3 校验代理模型精度
代理模型构建完成之后,需要对其精度进行评估和校验。通常根据以下2个准则来判断代理模型的精度[8]:复相关系数R2和均方根误差(Root Mean Square Error,RMSE),其表达式为
(16)
(17)
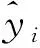
R2越接近1,表示代理模型的全局近似程度越好,一般认为大于0.9即满足要求,此处R2为统计学符号,并非平方,其值可能为负;RMSE越接近0,表示最大的局部误差越小,一般认为小于0.2即满足要求。
空间飞越发射窗口的计算需要考虑多个约束条件,包括变轨速度增量、飞越时间、飞越点状态、飞越过程燃料等。其中飞越点状态约束包括飞越点位置和速度约束、飞越点光照条件约束等;飞越过程燃料约束是为了保证飞越点精度,进行中途修正所需的燃料约束。
3 两种代理模型方法的对比
针对本文研究的空间飞越过程中初始条件对发射窗口影响的问题,利用1.2节提出的数值计算方法,根据代理模型技术构造RBF模型和Kriging模型,对2种模型的精度进行对比分析。
设t0时刻飞越航天器和目标航天器的轨道根数如表1所示。表中,a为半长轴,e为偏心率,i为轨道倾角,Ω为升交点赤经,ω为近地点幅角。
覆盖在顶管上的载荷主要由管节上方土压力和道路交通载荷组成,管节上方土压力主要与覆土深度和土层有关,在考虑卸荷拱效应的作用下,采用散粒体的极限平衡理论的马斯顿法计算土压力,马斯顿法相比其他土压力理论方法考虑了土体内聚力的影响[1-2]。
采用全析因试验设计方法选取样本点。本文研究的是初始条件对发射窗口的影响,因此输入变量设为飞越航天器和目标航天器的平近点角mf0和mt0,因素数为2;在设计空间[0°,360°)内以10°为步长取值,因素数为36;因此是一个2因素36水平的试验设计问题,样本点数ns=362=1 296。
计算出每个样本点所对应的输出值,利用输入/输出样本数据x、y构建RBF模型和Kriging模型。
为校验代理模型的精度,在设计空间内随机选取200个测试样本点,计算2个代理模型的R2和RMSE。计算结果如表2所示。
从表2可以看出,以R2和RMSE 2个准则来判断,RBF模型的精度都高于Kriging模型。测试样本点的预测值与真实值的对比如图4所示,图中的点越靠近对角线,表示该点的预测值与真实值越接近。可以看出,相对于Kriging模型,RBF模型的点在对角线附近更集中,精度更高。

表1 t0时刻轨道根数Table 1 Orbit elements at moment t0

表2 两种代理模型精度对比Table 2 Accuracy comparison of two surrogate models
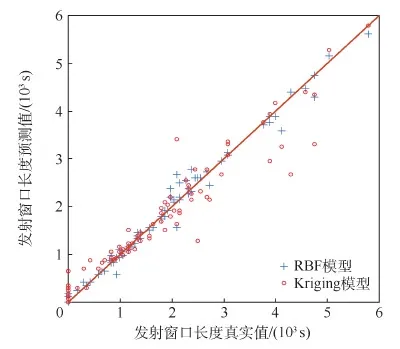
图4 测试样本点分布Fig.4 Distribution of test sample points
因此,本文采用RBF模型研究空间飞越过程中初始条件对发射窗口影响。
4 实例验证
以表1中的轨道根数为例,基于RBF模型进行分析。计算发射窗口时,变轨速度增量约束Δvmax=500 m/s,飞越时间约束Δtsmax= 9 000 s。
提高计算效率、减小计算耗时是本文研究代理模型的初衷和目的,因此首先检验应用代理模型后计算时间上的变化。根据第1节中的分析,在设计空间内以1°为步长使用真实模型进行计算,预计耗时约60 h,计算时间过长。因此以2°为步长使用真实模型和代理模型分别进行计算,计算时间如表3所示。
从表3可以看出,使用RBF模型计算发射窗口耗时仅为使用真实模型的0.29%,计算效率得到极大提高。使用代理模型之前需要先进行构建,因为在构建和校验精度时需要大量样本数据,而这些样本数据是通过使用真实模型计算得出的,所以需要花费一定的时间。但总计算时间也仅为使用真实模型的6.31%,相比而言效率还是较高。而且代理模型的构建是一次性的,一旦构建完成,对于相同轨道根数情况的计算就可以重复使用,无需再次构建。
代理模型除了极大地提高计算效率外,还需要满足一定的精度要求。表2中的数据显示,RBF模型的R2>0.9,RMSE<0.2,均满足要求。为直观显示其应用效果,绘制发射窗口长度相对于平近点角mf0和mt0的等值线图,如图5所示。可以看出,应用RBF模型计算得到的等值线图与使用真实模型得到的结果基本相同,可以反映出初始条件对发射窗口的影响。
通过对等值线图分析可以看出:
1) 对于飞越航天器和目标航天器为非共面圆轨道的情况,发射窗口长度取决于初始时刻两者的平近点角,平近点角之差相同并不能保证发射窗口长度相同。图6中的虚线为两者平近点角之差为零的点的集合,这些点对应的发射窗口长度不等,最长为2 204.4 s,最短为0 s。
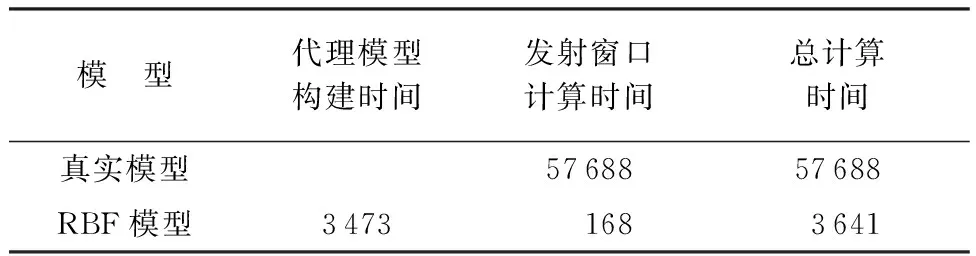
表3 代理模型和真实模型计算时间对比Table 3 Comparison of calculation time between surrogate model and true model s
2) 对于任意的mf0,都存在对应的可行mt0区间,使发射窗口存在,即当目标航天器位于该区间内时,飞越航天器在速度增量和时间约束下能够实现飞越。不同的mf0对应的mt0区间不同,区间长度108°~172°;同样,对于任意的mt0,都存在mf0区间,区间长度108°~188°。如图7所示,当mf0=160°时,可行mt0区间为[40°,158°],区间长度118°;当mt0=160°时,可行mf0区间为[162°,288°],区间长度126°。
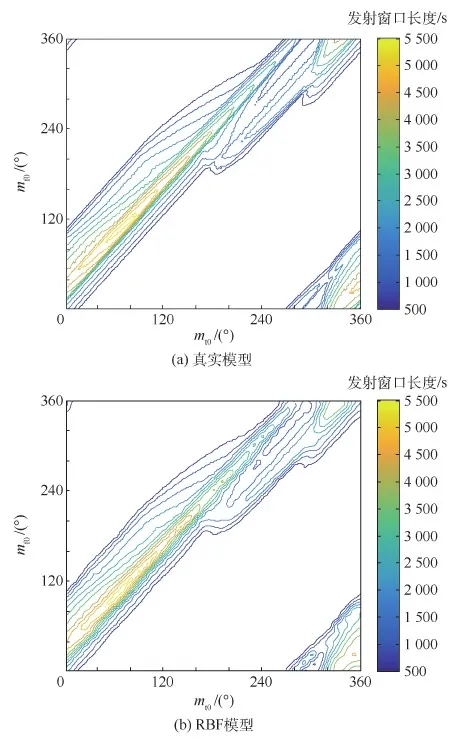
图5 真实模型和RBF模型的发射窗口长度等值线图Fig.5 Contour map of launch window length of true model and RBF model
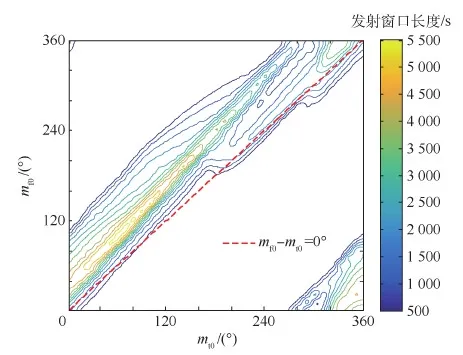
图6 平近点角相等时的发射窗口长度Fig.6 Launch window length of equal mean anomalies
3) 从图5能够直观地看出发射窗口长度的分布情况和变化趋势,可以选取发射窗口较长的点,在实施空间飞越任务时将其作为初始条件。从图5(b)可以看出,当以mf0=112°、mt0=72°为初始条件时发射窗口最长,为5 743.1 s。而飞越航天器的轨道周期为5 801.1 s,这意味着在一个周期之内基本都可以实施飞越。
4) 对任意一点,可以根据图5直接判断其是否具备飞越条件及其发射窗口长度;若以某点为初始条件的发射窗口为0,则可以判断出多长时间后可以具备飞越条件。如图8所示,A点对应的mf0和mt0为(40°,80°),以其为初始条件,发射窗口为0,根据飞越航天器和目标航天器的轨道根数,两者平均角速度n1/n2=1.2,则两者的位置随时间的变化在图上表示为以A为起点、斜率为1.2的线段,如图中的虚线所示。可以看出,经过2 526.2 s后虚线与等值线图首次相交于B点,以该点为初始点发射窗口长度为500 s;若要求发射窗口长度不少于某值,如2 000 s,则需要从A点起经过4 124.6 s后到达C点,以C点为初始条件开始飞越。以A点为起点,发射窗口长度随时间变化如图9所示。
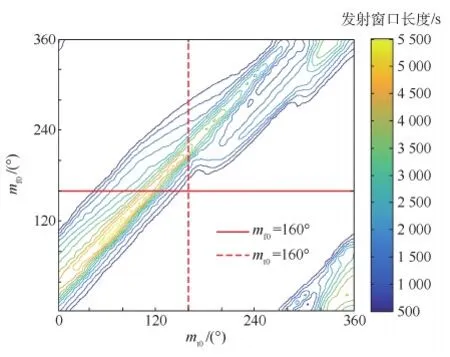
图7 可行的平近点角区间示意图Fig.7 Schematic diagram of feasible region of mean anomaly
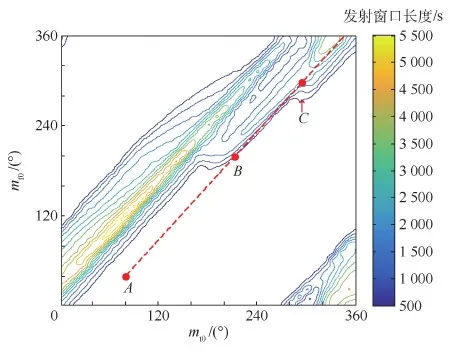
图8 任意一点的发射窗口分析Fig.8 Analysis of launch window of one point
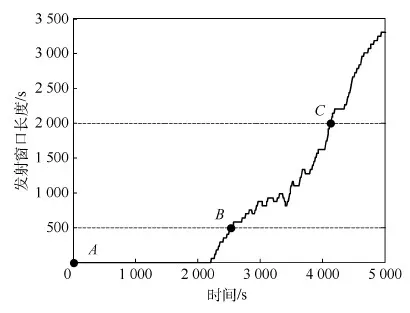
图9 发射窗口长度随时间的变化Fig.9 Change of launch window length with time
5 结 论
1) 本文分析了空间飞越任务流程,建立了用于分析初始条件对发射窗口影响的数值计算模型,该模型包含4个变量的循环,计算耗时约60 h,效率较低。
2) 研究了代理模型技术,采用全析因试验设计方法生成样本数据,构建了RBF模型和Kriging模型,以R2和RMSE准则对比了2种模型的精度,结果表明RBF模型精度较高。
3) 应用RBF模型计算发射窗口长度,计算耗时仅为真实模型0.29%,而且精度校验满足要求。根据发射窗口长度的等值线图,分析了初始条件对发射窗口的影响。
4) 后续可以在2个方面进一步开展研究:一方面,提高发射窗口计算模型的精度,如采用高精度轨道动力学模型,考虑飞越点状态约束、飞越过程燃料约束等;另一方面,提高代理模型的效率和精度,如改善样本点选取方法来减少构建代理模型的成本,研究代理模型的更新和修正方法来提高模型精度等。
