纳卫星电磁对接机构技术

慕忠成， 叶东， 吴树范，*

(1. 上海交通大学航空航天学院, 上海 200240； 2. 哈尔滨工业大学航天学院， 哈尔滨 150001)

随着微电子、微机械系统和集成电路的快速发展，卫星小型化技术有了大幅进步。在此背景下， 1999年，斯坦福大学的Bob Twiggs提出立方星，引起了广泛关注[1]。立方星形状如名，是边长为10 cm的立方体，输出功率相当于手机，在几瓦范围内，重量不足1.3 kg[1-2]。立方星大量采用货架产品，具有成本低、研制周期短、扩展性强等特点，一般应用于小型试验、对地观测和业余无线电通信等。统计显示，2013—2015年，274颗立方星已成功发射。2014年，立方星被《科学》杂志评选为10大科学突破之一。一方面，随着载荷技术的提升，立方星空间应用得到拓展，已经开始由“试验应用型”向“业务服务型”转变[3-5],另一方面，在轨重构和在轨组装引起越来越多研究人员的关注。然而传统的在轨交汇对接技术主要通过推力器配合相应敏感器实现，在近距离对接阶段，为避免碰撞，控制精度要求相对比较高，并且容易产生羽流污染和冲击力等方面的问题。对此，利用电磁技术实现在轨交汇对接成为近几年研究热点，尤其是针对电磁对接中的动力学及控制问题[6-10]。对比基于推力器的对接方式，电磁对接技术不需要消耗燃料，且无对接冲击和羽流污染等优势[11]。但是，在现有技术条件下，由于其所能够提供的电磁力量级较小，仅适用微小型航天器的对接驱动需求[12-13]。

综上所述，电磁对接技术与立方星技术的结合，不仅弥补了当前电磁对接技术的缺陷，而且进一步促进了立方星空间应用，增强立方星空间重构特性，一定程度上补偿软件重构的不足。利用电磁对接技术，具有模块化标准化特性的立方星可以像乐高积木一样，进行空间自主分离和重组。本文以此为背景，首先，结合立方星自身约束，设计出一种适用于立方星的低成本电磁对接机构。然后，通过理论分析，给出了适用于工程应用的电磁力和电磁力矩模型，并通过数值仿真方法，研究了铁芯的影响，以此来弥补理论分析的不足。

1 电磁对接机构设计

电磁对接的主要特征是电磁体之间的作用力随距离的增加而减小，其量级与电磁体材料与结构密切相关[8]。在距离范围、功耗、质量等约束下，适用于微纳卫星编队飞行与交会对接所需大小的电磁力/力矩，当前主要存在2种电磁力产生方式：一是采用“超导线圈”；二是在普通线圈中加铁芯以增加电磁力[14-15]。

超导体材料对热环境的要求比较苛刻，在地面试验中需要采用液氮冷却，在太空中需要设计专门的热系统进行制冷，从而增加额外的制冷设备和功耗，不适用立方星。螺线管中插入铁芯可以增加磁场磁通量，并且结构简单、功耗小，适用于立方星。对此，本文以螺线管电磁铁作为电磁对接机构的设计基础，设计了一种适用于1U立方星结构的电磁对接机构。

电磁对接机构由2部分组成，一部分为能够产生对接驱动力的电磁装置，另一部分为用于对接和锁紧的对接端口。考虑到立方星尺寸限制，2部分均秉承结构简单、占用空间小设计原则。电磁装置采用含铁芯的直流螺线管式电磁铁结构，选择软磁材料1J50作为铁芯，其具有低矫顽力和高磁导率、易于磁化和退磁等优势，减少了由于剩磁原因对卫星姿控系统的影响。

螺线管电磁铁直径、长度、线圈匝数等主要通过卫星本身体积约束、功耗约束以及发热平衡约束迭代设计获得，主要设计过程如图1所示。

首先，利用经验公式(1)～式(4)，获得圆形铜导线基本参数：

(1)

(2)

(3)

(4)

式中：In为安匝数，I为线圈电流，n为线圈匝数；P为线圈额定功率；A0为线圈窗口截面积；lav为线圈平均长度；U为线圈电压；Aa为线圈带绝缘导线截面积；dd为线圈带绝缘导线线径。

其次，通过发热平衡约束设计磁棒参数，磁棒参数包括磁芯材料、直径、长度及绕线后的外径。其中磁芯直径由纳卫星的重量和体积限制，长度由线圈长度确定，发热方程为

Pt=a1Sa+a2SM

(5)

式中：Pt为发热平衡功率；Sa和SM分别为与空气和金属接触的散热面；a1和a2分别为单位散热面上所散出的功率，是由线圈厚度和类型得到的经验值。

再次，基于上述约束，最终确定螺线管电磁铁设计参数：磁芯直径为10 mm，长度为97 mm。线圈直径为0.65 mm，绕线长度为88 mm，线圈匝数为975±5，线圈厚度为5 mm。绕制完成的螺线管电磁铁如图2所示。

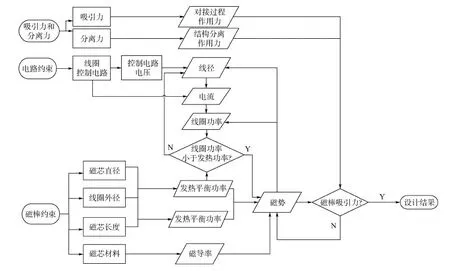
图1 螺线管电磁铁设计参数获取过程Fig.1 Gaining process of solenoid electromagnet design parameters

电磁对接机构采用“类杆-锥式”对接方式，此类对接方式对比异体同构周边式对接机构，结构更加简单、质量较轻、使用可靠且应用广泛，适用于纳卫星。对接端口分为对接杆和接纳锥2部分，分别安装于主动卫星和被动卫星，如图3所示。对接杆与接纳锥通过螺线管电磁铁所产生的磁力驱动近距离对接过程。采用“笔帽式”锁紧方式进行锁紧，对接杆外部有一圈球状挡位，接纳锥的内部有3个半球状卡扣，当对接杆进入接纳锥内部时，在轴向力的控制下，对接杆外部与接纳锥内部可通过球面接触实现对接锁定与脱离。卡扣与挡位均由弹性材料制备，当对接杆进入接纳锥后，对接杆上的挡位与接纳锥内的卡扣相互接触挤压，发生弹性变形。变形后的挡位和卡扣在材料恢复力的作用下使对接杆上的挡位与接纳锥内的卡扣相互夹紧。该锁紧原理机械结构简单、质量轻、体积小、对控制精度要求低，适用于纳卫星，对接过程如图4所示。

图2 含铁芯的螺线管电磁铁Fig.2 Solenoid electromagnet with iron core

图3 锁紧机构示意图Fig.3 Schematic diagram of locking mechanism

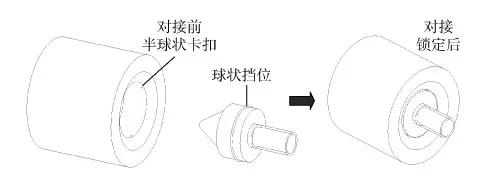
图4 对接锁紧过程Fig.4 Docking locking process

最后，基于自由度约束准则，采用3组对接端口分布于同一圆周设计布局，实现主动卫星与被动卫星之间6个自由度的动力学约束，如图5所示,F为自由度。

综上所述，基于螺线管电磁铁、对接端口以及1U立方星优化布局3个方面的分析设计，实现了1U电磁对接机构的设计，如图6所示。

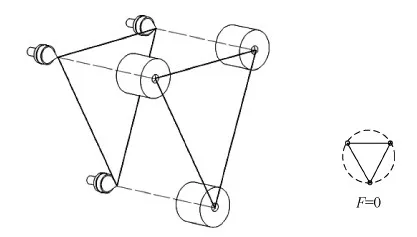
图5 自由度约束设计Fig.5 Freedom degree constraint design

图6 1U电磁对接机构实物图Fig.6 Picture for 1U electromagnetic docking mechanism

2 电磁力/力矩模型简化

2.1 通电螺线管模型的简化

针对第1节电磁对接机构，对电磁力/力矩模型进行简化，将有限长通电螺线管模型简化为单匝线圈模型，通电线圈与通电螺线管模型如图7所示。

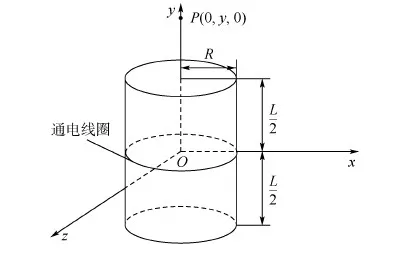
图7 通电线圈与通电螺线管模型Fig.7 Electrified coil and solenoid model

对单匝线圈与通电螺线管在轴线上所产生的磁场进行对比分析。单个线圈轴线上磁场表达式为

(6)

通电螺线管轴线上磁场表达式为

(7)

式中：μ0=4π×10-7N/A2为真空磁导率；R为电流线圈的半径；L为通电螺线管长度。

分析结果表明：在距离较远时，两者相差不大，在距通电螺线管端部中心距离d在0.2～1 m之间，可以认为两者的比值c=B1/B2=0.2，如图8所示。

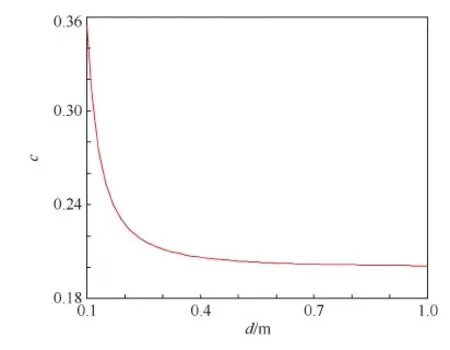
图8 通电螺线管与单个线圈轴线上磁场比值Fig.8 Magnetic field ratio between electrified solenoid and single coil axis

2.2 精确模型和远场模型

通过毕奥-萨伐尔定理，利用多重积分可得到精确的单个线圈电磁力模型，但该模型非解析，因此本文采用泰勒一阶展开式进行简化近似。电磁对接机构空间位置示意图如图9所示，a1、a2、a3、a4为航天器a的4个通电螺线管，b1、b2、b3、b4为航天器b的4个通电螺线管，d1为每一个螺线管间距，2个航天器间距相同。

精确电磁力和电磁力矩为

(8)

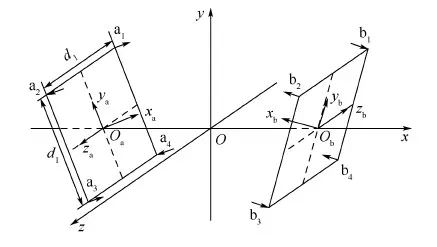
图9 电磁对接机构空间位置示意图Fig.9 Schematic diagram of spatial position for electromagnetic docking mechanism

式中：dla和dlb为线圈矢量微元；r为线圈微元到空间点的距离。

通过泰勒一阶展开而简化的远场电磁力和电磁力矩为

(9)

式中：d为两航天器的相对距离矢量，下标ba表示从航天器b指向航天器a；μ为磁矩矢量，下标a和b分别表示航天器a和航天器b。

为比较分析2种模型，本文从强度和角度2方面进行误差特性分析，基本方程如式(10)～式(13)所示，其中Δ1和Δ2分别表示电磁力强度误差和角度误差，Δ3和Δ4分别表示电磁力矩强度误差和角度误差。

(10)

(11)

(12)

(13)

一方面，针对电磁力，对2种模型进行比较分析，仿真分析结果表明，电磁力强度以及角度的误差相对于卫星之间距离呈现递减趋势(见图10～图13)。2个卫星的角度在10°以内时，在d≥0.1 m的条件下，强度和方位的误差分别在2%和1°以内。则存在以下合理的假设：远场电磁力模型成立的条件为d≥0.1 m。需要特别说明的是：α和β分别为2个螺线管线圈截面在y方向和z方向的初始夹角，坐标系的定义如图9所示。

另一方面，针对电磁力矩模型，对其进行了同样的误差分析，结果表明，远场模型的电磁力矩强度误差随着相对距离的减小而逐渐增大，呈现出与精确模型一样的趋势。2颗卫星的角度在10°以内时，当d≥0.1 m，强度误差Δ3均小于3%。方位误差的变化具有比较大的波动，但在距离满足d≥0.1 m的条件下，误差均小于1.5×10-6°。

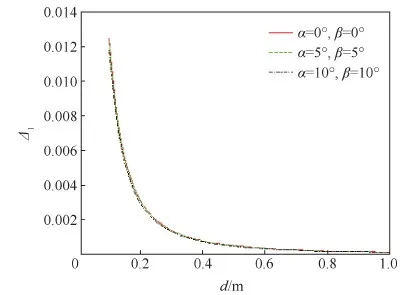
图10 电磁力强度误差与距离及角度的关系Fig.10 Change of strength error of electromagnetic force with distance and angle

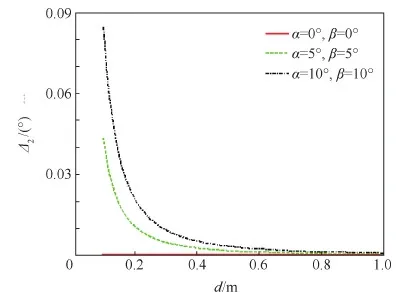
图11 电磁力角度误差与距离及角度的关系Fig.11 Change of angle error of electromagnetic force with distance and angle

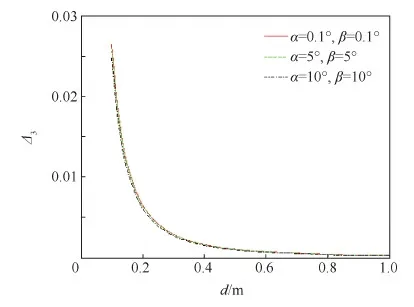
图12 电磁力矩强度误差与距离及角度的关系Fig.12 Change of strength error of electromagnetic moment with distance and angle

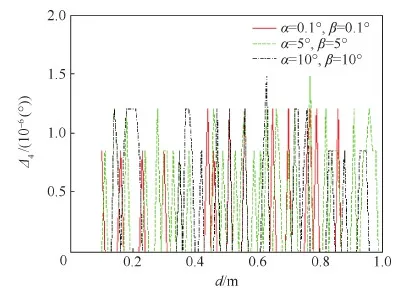
图13 电磁力矩角度误差与距离及角度的关系Fig.13 Change of angle error of electromagnetic moment with distance and angle

综上分析，当对接距离大于0.1 m时，远场模型与精确模型的误差是在工程应用可接收范围内，而本文设计的电磁对接机构，在完成对接情况下，中心距离恰为0.1 m，进而说明远场模型适用于本文所设计的电磁对接机构。

3 铁芯对螺线管电磁铁的影响

由于理论推导的复杂性，在第2节分析中并没有考虑铁芯的影响，对此本文进一步通过数值仿真分析方法，对铁芯的影响进行了分析。

图14给出了Maxwell 3D仿真模型。分析结果表明(见图15)，单一螺线管在轴线方向磁场强度分布均匀，但对于含铁芯的螺线管在轴线方向磁场强度峰值现象明显，成对称式分布。两者电磁强度相差明显，插入铁芯的螺线管电磁强度显著增加。

同时，为了定量的给出2种模型磁感应强度的不同， 本文对单个线圈和含铁芯的通电螺线管进行了比较分析，分析结果如图16所示。在距离对接中心较近时，两者比值约在10-4量级；随着距离的增加，2个模型的比值约在10-8量级。此分析结果可对远场模型进行修正，弥补远场模型没有考虑铁芯而产生的误差。

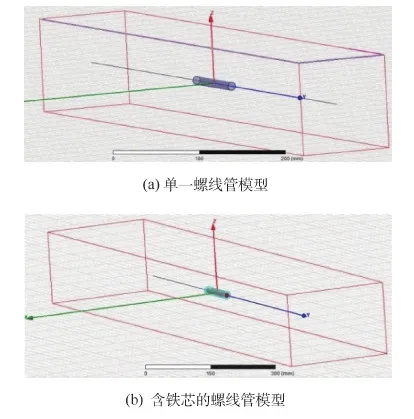
图14 2种螺线管Maxwell 3D仿真模型Fig.14 Two kinds of Maxwell solenoid 3D simulation model

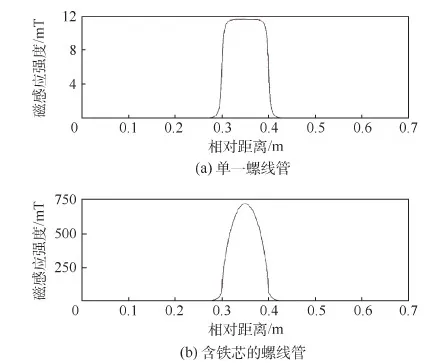
图15 单一螺线管和含铁芯螺线管轴线上磁感应强度分布Fig.15 Magnetic induction intensity distribution in axial direction for electrified solenoid with single solenoid and iron core

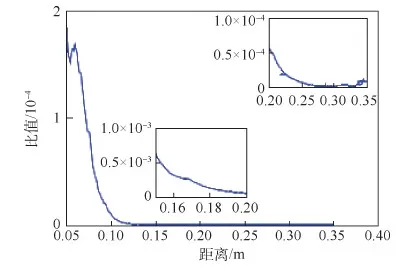
图16 单个线圈与通电螺线管磁感应强度比较分析Fig.16 Magnetic induction intensity comparison analysis between single coil and electrified solenoid

4 结 论

1) 本文基于电磁原理，在立方星约束条件下，设计了一种1U立方星电磁对接机构。

2) 创新性提出了一种“笔帽式”锁紧对接端口。

3) 通过对电磁力和力矩精确模型和远场模型的比较分析，明确了远场模型的范围。

4) 进一步，利用数值仿真分析方法，给出了铁芯对磁感应强度的影响，为理论分析的经验纠正奠定了基础。