基于指数平滑及差分处理的粮食产量组合预测方法
2019-01-12傅洪亮王少航曹培格杨铁军
傅洪亮, 王少航, 曹培格, 樊 超, 杨铁军
(河南工业大学 a.信息科学与工程学院; b.粮食信息处理与控制教育部重点实验室, 河南 郑州 450001)
粮食对于经济发展和社会稳定十分重要,我国是一个农业大国,粮食产量的多少、能否满足需要,一直是各级政府关注的主要问题之一,因此预测粮食产量对指导粮食生产具有重要的意义[1-2]。目前用于粮食产量预测的方法很多,主要有时间序列的回归方法[3]、BP神经网络法[4]、灰度预测法[5]及多元线性回归预测法[6]等。受多种因素的影响,粮食产量的时间序列具有非平稳性,而传统预测方法的预测精度不高,鲁棒性不强。
本文在研究灰色理论及多元回归的基础上,提出一种基于指数平滑及差分处理的粮食产量组合预测方法,在分析与处理粮食作物播种总面积、总劳动力、化肥总用量、有效灌溉面积、用电总量、机械总动力、受灾总面积等数据的基础上,运用多元线性回归及残差修正方法对中短期(5年)和中长期(10年)全国及河南省的年度粮食总产量进行预测。
1 灰色理论与多元线性回归
1.1 灰色理论
灰色理论由华中理工大学邓聚龙教授于20世纪80年代创立。该理论以部分已知信息、部分未知信息的“少数据”“贫信息”不确定性系统为研究对象,通过对部分已知信息的挖掘,提取有价值的信息,实现对系统运行行为、演化规律的正确描述和有效监控[7]。
目前使用比较广泛的灰色预测模型是关于数列预测的一个变量、一阶微分的GM(1,1)模型[7]:
设时间序列X(0)有n个观测值,X(0)={X(0)(1),X(0)(2),…,X(0)(n)},通过累加生成新序列X(1)={X(1)(1),X(1)(2) ,…,X(1)(n)},则GM(1,1)模型相应的微分方程为:
(1)
式中:a为发展灰数。
待估参数向量为α,α=[aμ]T。通过最小二乘法求解可得:
α=(BTB)-1BTYn
(2)
式中:
求解微分方程式(1),可得预测模型:
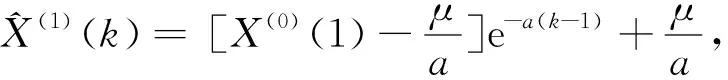
(3)
有预测公式:
(4)
1.2 多元线性回归
设系统中有m个输入变量(影响因子)x1,x2,…xm,输出为Y,可建立输入与输出之间的如下关系模型:Y=f(x1,x2,…xm)。考虑到该函数的复杂性,通常用Volterra级数展开的多项式去逼近[8-10]。该多项式为:
(5)
进一步简化式(5),可得多元一次方程:
Y=a0+a1x1+a2x2+…aixi
(6)
式中,ai可通过线性回归求得,i=0,1,2,…,m。
2 指数平滑及差分处理组合预测
2.1 预测方法
本文提出的组合预测方法首先对影响粮食产量的因素(包括粮食作物播种总面积、总劳动力、化肥总用量、有效灌溉面积、用电总量、机械总动力、受灾总面积等)进行分析,对影响因子的以往数据进行指数平滑处理,运用灰色理论,通过迭代预测影响因子的新数据,预设一个阈值后,通过影响因子关联度分析,自动选取关联度大的因子,对以往粮食产量数据进行差分处理,运用多元线性回归及残差修正预测未来的年度粮食产量。其预测流程如图1所示。

图1 指数平滑及差分处理组合预测的流程
2.2 预测步骤
首先运用灰色理论预测影响粮食产量的因子。
步骤1:对往年粮食产量影响因子的数据进行差分运算,计算影响因子相邻数据的波动量。相邻数据的波动量为:
(7)
如果某一波动量绝对值大于整体平均波动量z(z=Average(|z(k)|)),则此时数据用前一数据加上(或减去)整体平均波动量来代替,x(k)=x(k-1)+(1+Sign(z(k))×z。这里:Average()表示取平均运算;Sign()表示取符号运算。
步骤2:对步骤1处理过的数据进行指数平滑处理,以进一步减小数据的波动。指数平滑处理公式如下:
x′(k)=ex(k)
(8)
步骤3:运用式(1)~式(4)及处理过的往年粮食产量影响因子的数据x′(k),预测未来若干年的影响因子数据。然后运用预测的未来影响因子数据和多元回归方法预测粮食产量。
步骤4:对往年粮食产量及影响因子数据进行初始像和一阶缓冲算子运算。其目的在于归一化及平滑处理数据。
初始像为:
(9)
一阶缓冲算子为:

(10)
步骤5:计算粮食产量和影响因子间的关联系数,即:
(11)
步骤6:筛选关联系数大的影响因子。为了提高预测精度,只保留关联系数大于0.8的影响因子。

步骤8:进行步骤4的逆运算。
一阶缓冲算子逆运算如下:

k′=N,N-1,…,n,n-1,…,3,2,1
(12)
初始像逆运算如下:
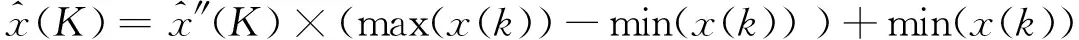
K=n,n+1,…,N,k=1,2,3,…,n
(13)
步骤9:残差修正。将预测的粮食产量与往年的实际产量之差作为输入数据,运用灰色理论(按步骤4)预测未来若干年的粮食产量误差,再运用此误差修正未来若干年的年度粮食总产量。
步骤10:计算粮食产量预测相对误差。
步骤11:完成预测。
3 组合预测的结果与分析
基于全国及河南省粮食总产量以及影响粮食产量的主要因素(包括粮食作物播种总面积、总劳动力、化肥总用量、有效灌溉面积、用电总量、机械总动力、受灾总面积)对应于1978~2013年的数据,进行预测验证。
针对5年以内的中短期预测,用1978~2008年共31年的数据预测2009~2013年的产量并做验证;10年以内的中长期预测,用1978~2003年共26年的数据预测2004~2013年的产量并做验证。本文对灰色预测、指数平滑及差分处理组合预测(无残差修正,DI-AFS多元预测)和指数平滑及差分处理组合预测(有残差修正,DI-AFS-EM多元预测)3种方法进行比较,预测结果如图2~图5所示。

(a) 产量预测值

(b) 各年度相对误差

(c) 粮食产量影响因子关联系数

(d) 平均相对误差图2 用31年数据预测5年中短期全国粮食年度总产量的结果




图3 用31年数据预测5年中短期河南省粮食年度总产量的结果




图4 用26年数据预测10年中长期全国粮食年度总产量的结果

(a) 产量预测值

(b) 各年度相对误差

(c) 粮食产量影响因子关联系数

(d) 平均相对误差图5 用26年数据预测10年中长期河南省粮食年度总产量的结果
比较3种方法的预测结果可知,无论是中短期预测(5年)还是中长期预测(10年),指数平滑及差分处理组合预测在预测精度上要好于灰色预测。这是由于预测时对数据的预处理使得数据的波动量减小,并且预测中考虑了全部的影响因素。另外,从图2~图5还可以看出,带有残差修正的指数平滑及差分处理组合预测可进一步提高预测精度。
4 结 语
为了进一步提高粮食产量的预测精度,增强预测算法的鲁棒性,本文在研究灰色理论及多元回归的基础上,提出了一种基于指数平滑及差分处理的粮食产量组合预测方法。该方法首先对影响粮食产量的因素进行分析,对影响因子的以往数据进行指数平滑处理,运用灰色理论,通过迭代预测影响因子的新数据;然后通过影响因子关联度分析,自动选取关联度大的因子,对以往粮食产量数据进行差分处理,以减小数据的波动;最后运用多元线性回归及残差修正预测未来粮食产量。对全国及河南省年度粮食总产量的中短期(5年)和中长期(10年)预测可知,本文提出的预测方法预测效果较好。
该算法可用于不同粮食品种的产量预测(如稻谷、小麦等),但通过实验得知,该算法对玉米的产量预测精度有待提高。由于玉米数据波动较大,因此其预处理方法还存在进一步改进的空间。
