地月空间对称自由返回轨道设计与分析

彭坤 孙国江 王平 徐明

(1 中国空间技术研究院载人航天总体部，北京 100094) (2 北京航空航天大学宇航学院，北京 100191)

随着“深空之门”(Deep Space Gateway)地月空间站方案的逐步完善[1]，国际各航天机构已将进入地月空间作为推动载人深空探测发展新的兴趣点，而地月空间人员往返运输途径则是研究的重点。不同于地月空间货运任务，人员往返运输首先要考虑人员安全性。自由返回轨道由于其不需要额外变轨仅借助月球引力自动返回地球的特性，能保证航天器发生故障后航天员安全返回地球，而被广泛应用于“阿波罗”(Apollo)载人登月工程的地月转移过程中。Apollo-13任务[2]正是利用自由返回轨道的特性，使3名宇航员最终安全返回地球。Apollo-13任务[3]全面验证了自由返回轨道的正确性，被美国人称为“一次成功的失败”。我国于2014年发射的探月三期飞行试验器也采用了绕月自由返回轨道，并成功返回地球。

自由返回轨道的研究开始于20世纪Apollo计划时期，文献[4]采用双二体模型和圆锥曲线拼接方法求解绕月自由返回轨道。随后文献[5]结合圆锥曲线拼接和多体模型设计绕月自由返回轨道并进行参数对比。2010年，国内文献[6]基于双二体假设给出了自由返回轨道设计流程。文献[7]基于双二体模型先采用粒子群算法进行全局优化。文献[8]在双二体模型下以能量匹配计算初值，完成了自由返回轨道发射弹道拼接和落点位置匹配。文献[9]在双二体假设下通过4段二体轨道拼接完成自由返回轨道初值设计，用序列二次规划求解精确轨道和满足停泊轨道入轨相位的窗口。文献[10]在文献[8]求解思路基础上采用序列二次规划构造两层迭代格式进行求解。除了双二体模型外，圆型限制性三体模型也广泛应用于自由返回轨道求解。文献[11-12]基于圆型限制性三体模型定义了对称自由返回轨道，并系统研究了自由返回轨道的轨道优化问题。文献[13]以对称自由返回轨道为基础，通过改变近月点z轴方向的位置和速度求解满足不同出发点、近月点和返回点高度的自由返回轨道。伪状态模型[14-15]也可用于自由返回轨道初值求解。此外，文献[16]根据自由返回轨道的对称特性，直接在高精度模型中搜索自由返回轨道。

以上文献大多针对飞行时间为6天左右的Apollo式自由返回轨道，没有对整个地月空间不同近地点高度、不同近月点高度以及不同飞行时间的自由返回轨道进行全面分析。文献[17]在三体模型给出不同类型对称自由返回轨道的地月转移入射速度增量和飞行时间等轨道参数特性，但较少讨论其轨道生成方法。文献[18]以二体模型初值猜测和三体模型数值计算逐步生成满足近月点高度和再入约束的自由返回轨道，但求解过程较复杂。

为研究整个地月空间多类型自由返回轨道特性，本文直接在三体模型下进行求解，飞行时间由终端点航迹角自动确定，依据自由返回轨道对称特性仅将近月点的地心旋转系y轴速度作为控制变量，基于月球逃逸速度估计控制变量初值。同时，提出不同地心和月心运行方向的对称自由返回轨道搜索策略，采用微分修正算法进行求解并分析不同近地点高度和近月点高度下自由返回轨道的轨道特性，以选择适合地月空间人员运输任务的自由返回轨道类型。

1 系统模型

在圆型限制性三体假设下建立航天器在地心旋转系下的二维极坐标动力学方程[19]

(1)

式中：(r,θ,vr,vθ)为地心旋转系下航天器的极径、极角、径向速度和横向速度(如图1所示)；Rm=(r2-2drcosθ+d2)1/2为航天器的月心距，d=384 400 km为地月距离；μE和μM分别为地球和月球的引力常数；ω为月球公转角速度。式(1)可作为自由返回轨道设计的状态方程。

图1 地心旋转系

自由返回轨道的飞行过程如图2所示：航天器从地球停泊轨道A点出发，施加地月转移入射(Translunar Injection，TLI)速度增量ΔV，进入自由返回轨道；航天器地月转移飞行至近月点B时，距月面高度hB；航天器在月球附近借助月球引力改变飞行方向，之后沿月地转移轨道返回近地点C，对应的地面高度和航迹角分别为hC和γC。

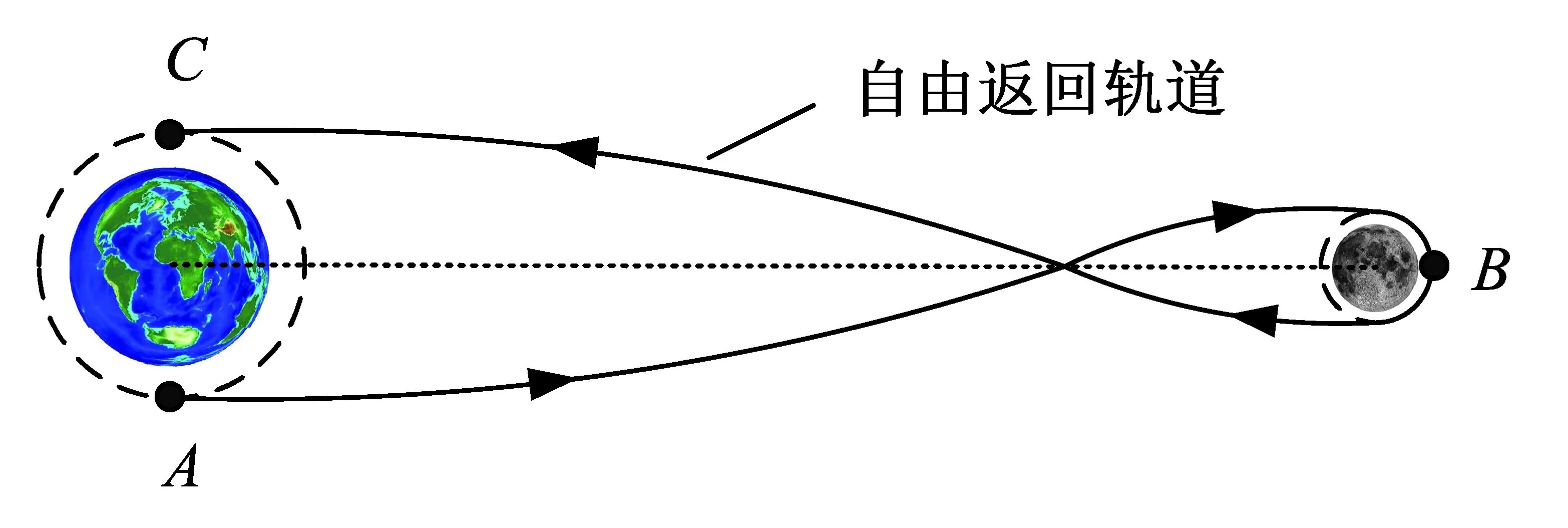
图2 自由返回轨道示意图Fig.2 Sketch map of free-return trajectory

对于自由返回轨道，设出发近地点A的初始时刻为tA，近月点B时刻为tB，近地点C时刻为tC，则其初始条件和目标约束可分别表示为

(2)

(3)

式中：RE和RM分别为地球和月球的半径；γ为航天器相对地球的航迹角；R和V分别为地心惯性系下航天器的位置速度矢量；rm和γm为航天器相对月球的极径和航迹角；Rm和Vm分别为月心惯性系下航天器的位置速度矢量。

2 对称自由返回轨道设计

2.1 求解模型

对于对称自由返回轨道，其出发点地心高度与返回点地心高度相等，航迹角均为0°。由文献[19]可知，对称自由返回轨道的近月点位于地心旋转坐标系x轴上。相比于一般地月转移轨道[20]，对称自由返回轨道的近月点约束更严格，敏感性更强，如果直接设计近地点状态，则收敛区间小，不易收敛。为此，本文以近月点参数作为控制变量，通过轨道逆推得到近地点状态以匹配出发点轨道参数，以降低自由返回轨道搜索过程敏感性。

根据对称自由返回轨道近月点位于地心旋转坐标系x轴上的特性可知，θ(tB)=0，vr(tB)=0。将近月点高度约束作为初始条件，以月心逆行为例，则r(tB)=d+RM+hB。唯一不确定的状态变量为vθ(tB)，可将其数值vθB作为控制变量。

为减少控制变量个数，提高搜索速度，不将近月点B到出发点A的轨道逆推的飞行时间tBA作为控制变量，而通过航天器相对地心的航迹角作为轨道逆推到出发点A的终止条件，如下式所示。

(4)

轨道逆推的终端约束为出发点的地心距r(tA)=RE+hA。通过以上转换，可将对称自由返回轨道求解转化为非线性规划问题，控制变量为vθB，目标约束为r(tA)=RE+hA，状态方程见式(1)，轨道逆推终止条件见式(4)。

2.2 初值估计

初值估计的精度直接影响自由返回轨道搜索的收敛性。本文以自由返回轨道近月点处月球逃逸轨道速度来近似估计控制变量vθB。

(5)

2.3 搜索策略

由于搜索流程大幅降低了自由返回轨道的敏感性，本文采用一般微分修正算法对自由返回轨道进行求解

(6)

式中：M=∂r(tA)/∂vθB，可通过线性摄动法数值计算得出，k表示当前迭代代数，k+1表示下一代迭代代数。

对于二维自由返回轨道，满足相同近地点轨道高度和近月点轨道高度的轨道共有4种类型：地心顺行月心逆行、地心逆行月心逆行、地心顺行月心顺行和地心逆行月心顺行。(与地心旋转系的旋转方向相同为顺行，反之为逆行。以图2为例，其描绘的自由返回轨道为地心顺行月心逆行轨道。)

对于月心顺行和逆行的情况，本文通过设置近月点时刻的极径大小来进行区分：

(7)

对于地心顺行和逆行的情况，使用出发点时刻极径约束不能直观进行区分，本文设置如下形式的出发点极径约束：

r*(tA)=Hz(tA)·r(tA)

(8)

式中：Hz(tA)为航天器在出发点时刻tA地心旋转系下角动量单位矢量的z轴分量，其正负可表征地心的顺逆行方向。通过以上定义，可通过修正的出发点极径r*(tA)来区分地心顺逆行：

(9)

2.4 算法流程

利用前述方法搜索自由返回轨道的步骤为：①根据自由返回轨道月心运行方向和式(7)设置近月点初始状态；②根据自由返回轨道地心运行方向和式(9)设置近地点终端约束；③由式(5)进行控制变量vθB初值估计；④以式(1)为状态方程从近月点B轨道逆推至近地点A，计算近地距r*(tA)的误差；⑤由式(6)修正控制变量vθB直至得到满足目标约束的自由返回轨道。最终得到的自由返回轨道即为指定月心和地心运行方向的自由返回轨道。

3 仿真验证

3.1 4种类型轨道搜索

设近地轨道高度hA=200 km，环月轨道高度hB=100 km，仿真动力学模型为圆型限制性三体模型(只含地球引力和月球引力)，采用以上自由返回轨道设计方法可快速搜索到4种不同地心和月心运行方向的自由返回轨道，如表1和图3～图6所示。由仿真结果可知，月心顺行自由返回轨道的飞行时间远大于月心逆行自由返回轨道，前者飞行轨迹长且远离地月空间，受太阳引力摄动影响更大；地心顺行自由返回轨道的地月转移入射速度增量略小于地心逆行自由返回轨道。

对于载人月球探测等需要再入地球的实际工程任务，自由返回轨道点A和点C不再对称，此时C点为再入点，航迹角γC为再入角，并不为0。以本文对称自由返回轨道求得的出发点A状态(θ(tA),vθ(tA))作为初值，进行微分修正迭代计算，即可得到满足再入约束的自由返回轨道。以地心顺行月心逆行轨道为例，对称自由返回轨道状态值为θ(tA)=227.24°，vθ(tA)=10.924 7 km/s。设再入高度hC=120 km，再入角γC=-6.0°，搜索到的满足再入约束的自由返回轨道实际状态值为θ(tA)=227.22°，vθ(tA)=10.924 8 km/s。由搜索结果知，初值非常接近真实值，搜索过程很快收敛。

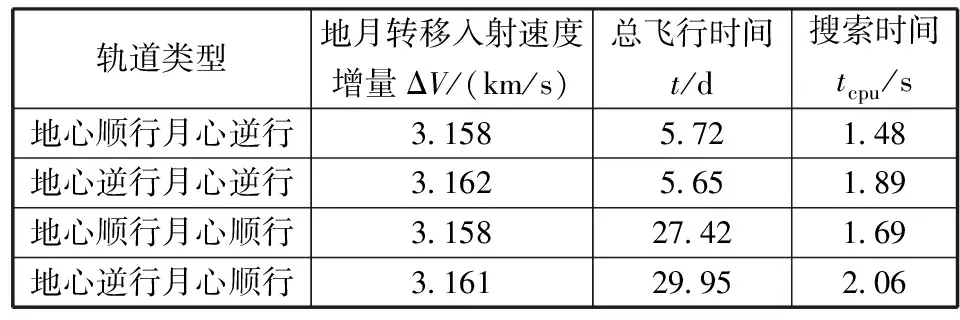
表1 4种类型自由返回轨道搜索结果

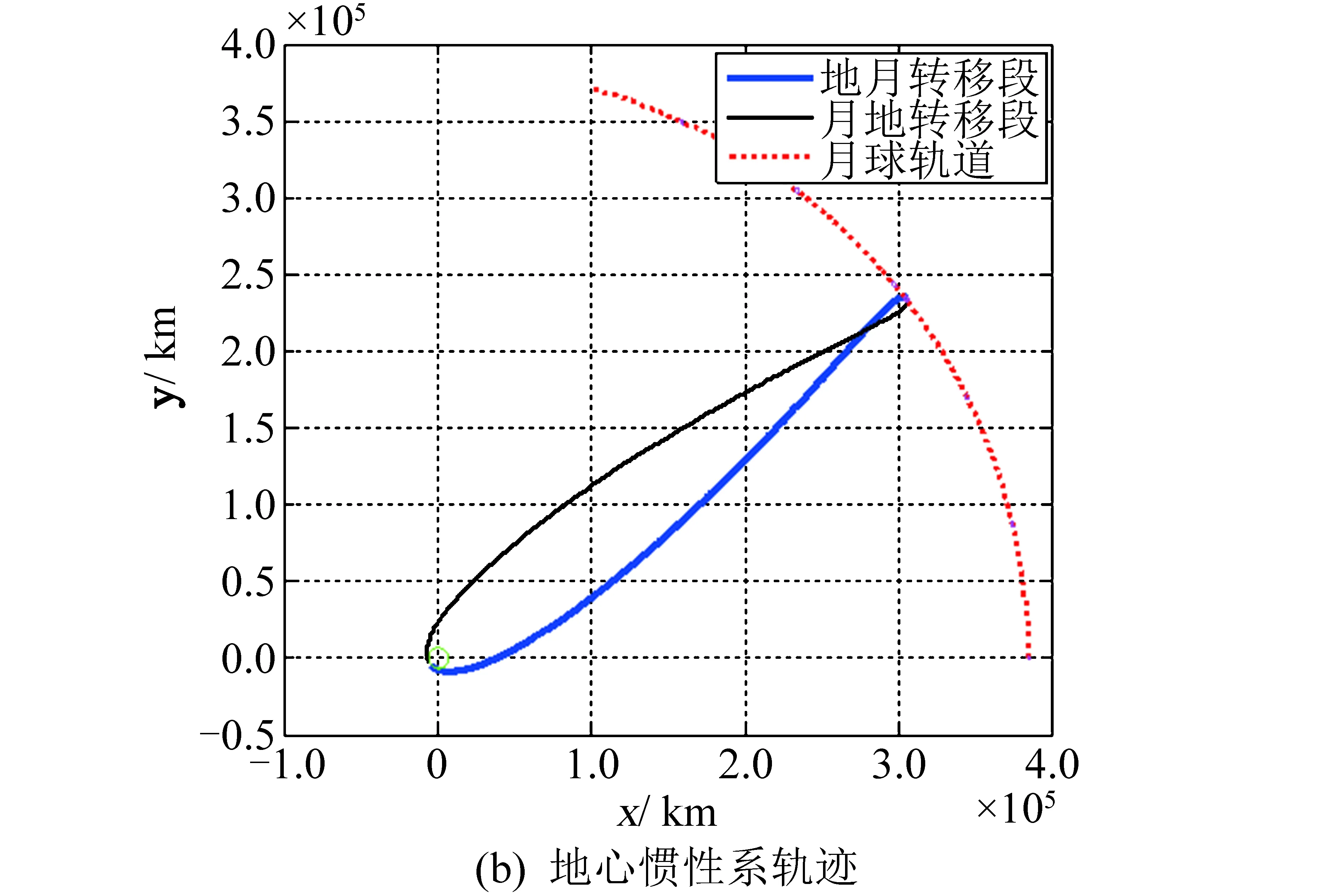
图3 地心顺行月心逆行对称自由返回轨道Fig.3 Symmetrical free-return trajectory with prograde in perigee and retrograde in perilune

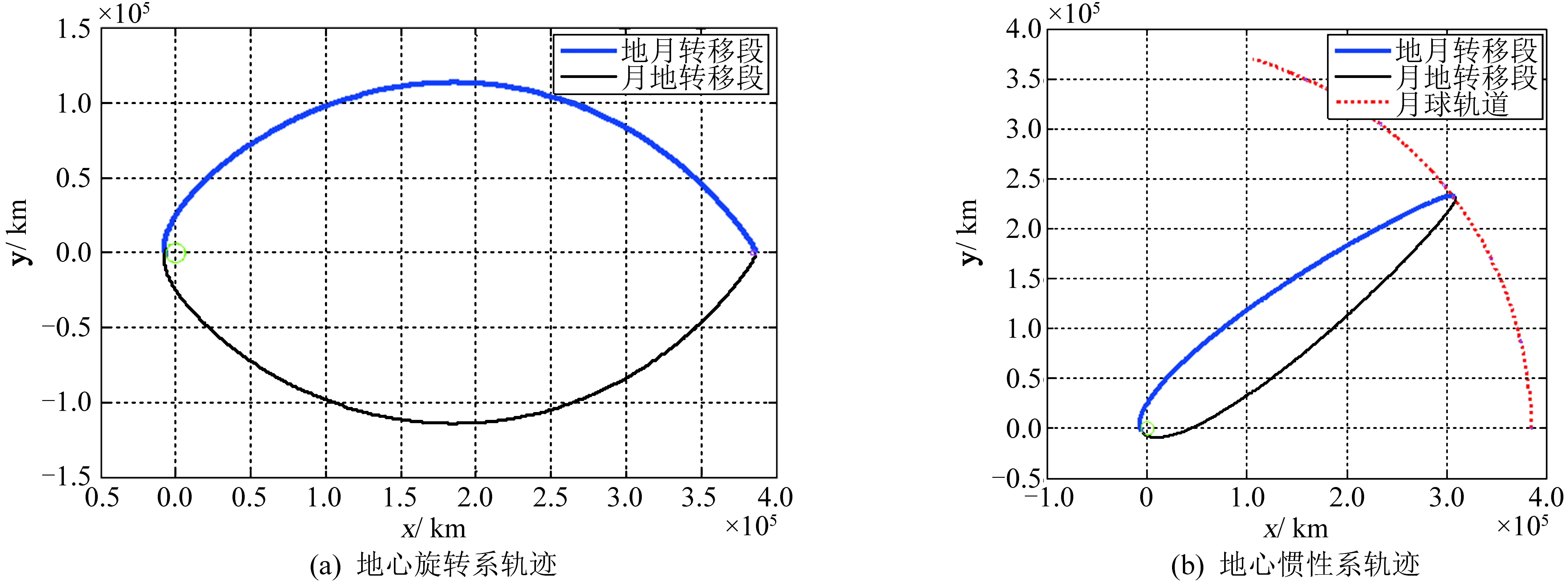
图4 地心逆行月心逆行对称自由返回轨道Fig.4 Symmetrical free-return trajectory with retrograde in perigee and retrograde in perilune

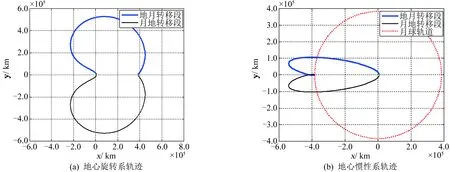
图5 地心顺行月心顺行对称自由返回轨道Fig.5 Symmetrical free-return trajectory with prograde in perigee and prograde in perilune

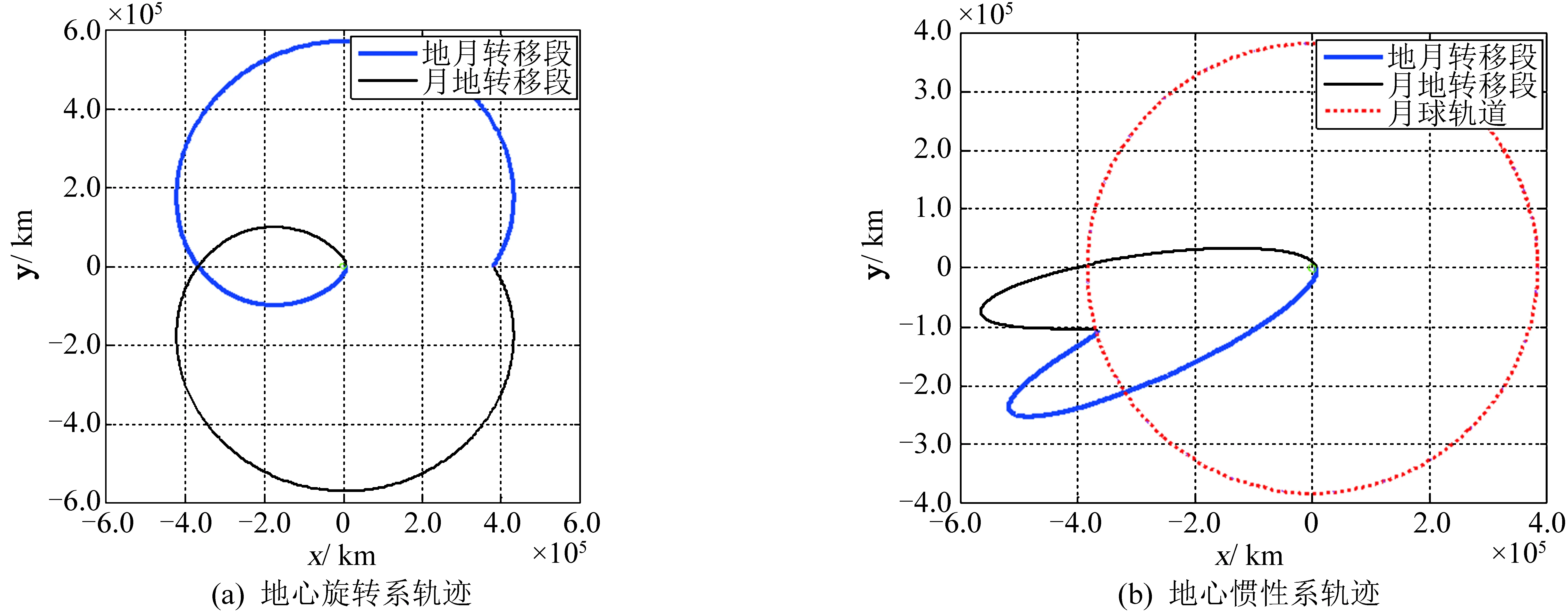
图6 地心逆行月心顺行对称自由返回轨道Fig.6 Symmetrical free-return trajectory with retrograde in perigee and prograde in perilune

3.2 轨道特性分析

考虑到未来地月空间可能在不同轨道高度的近地轨道和环月轨道分别设置空间站，应全面分析不同近地点高度和近月点高度的对称自由返回轨道的轨道特性。首先，设近月点高度hB=100 km，近地点高度范围为hA=200～35 786 km(LEO～GEO范围)，分析4种类型对称自由返回轨道的轨道参数随近地点高度的变化情况，如图7所示。由图7(a)可知，地月转移入射速度增量ΔV随近地点高度的增加而逐渐降低，变化范围约为3.2～1.1 km/s，4种类型轨道的ΔV数值相差不大。由图7(b)可知，总飞行时间随近地点高度的增加而逐渐增加，其中月心顺行轨道飞行时间远大于月心逆行轨道，前者飞行时间范围为27～38 d，后者飞行时间范围约为6 d。

其次，设近地点高度hA=200 km，近月点高度范围为hB=100～20 000 km，分析4种类型对称自由返回轨道的轨道参数随近月点高度的变化情况，如图8所示。由图8(a)可知，地月转移入射速度增量ΔV随近月点高度的增加而逐渐降低，变化范围不大，约为3.16～3.14 km/s，前期地心逆行轨道ΔV较大，后期月心逆行轨道ΔV较大，但总体来说量级相差不大。由图8(b)可知，月心顺行轨道总飞行时间随近月点高度的增加而逐渐减小，变化范围约为30～10 d；月心逆行轨道总飞行时间随近月点高度的增加而逐渐增加，变化范围约为6～10 d。

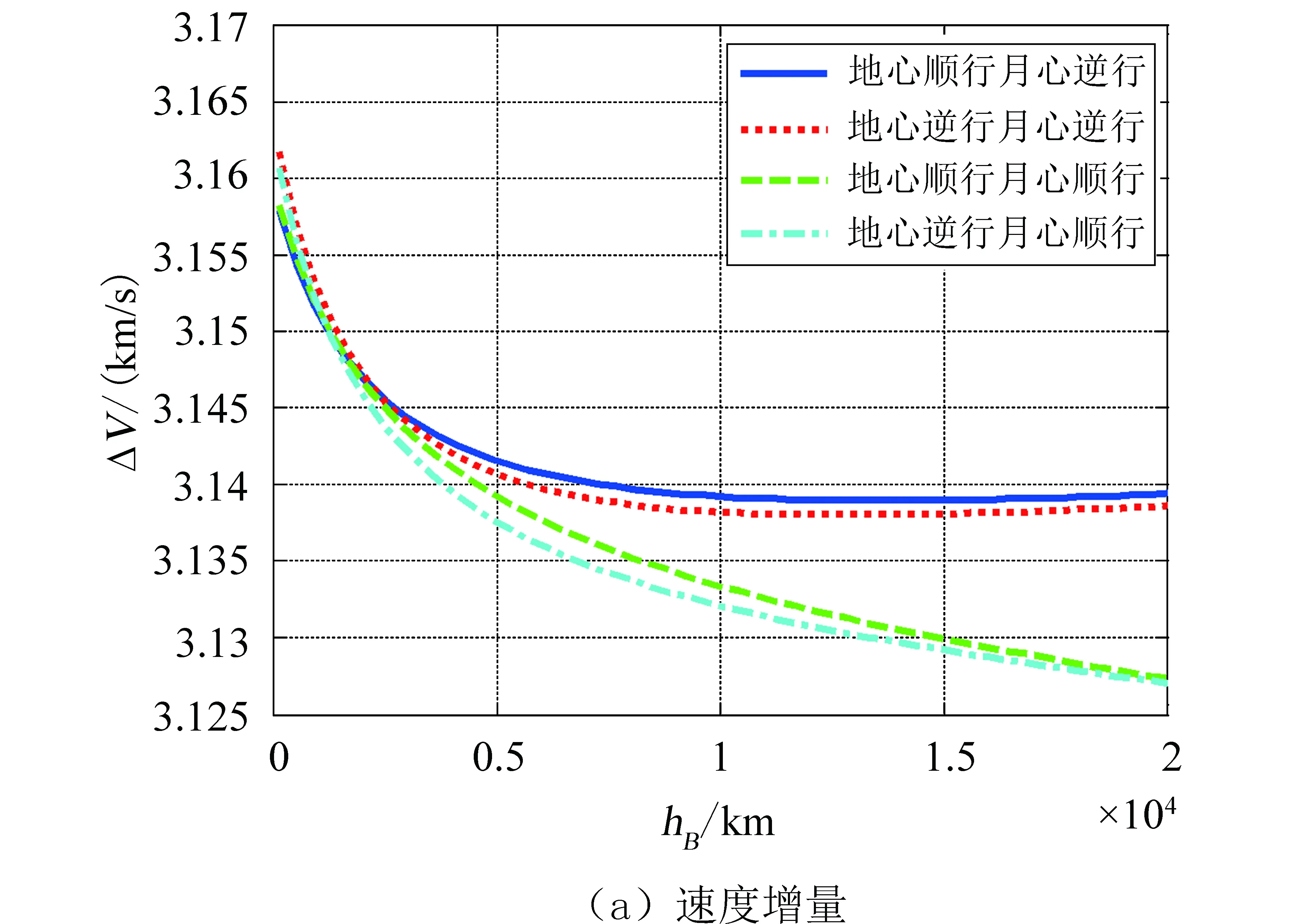
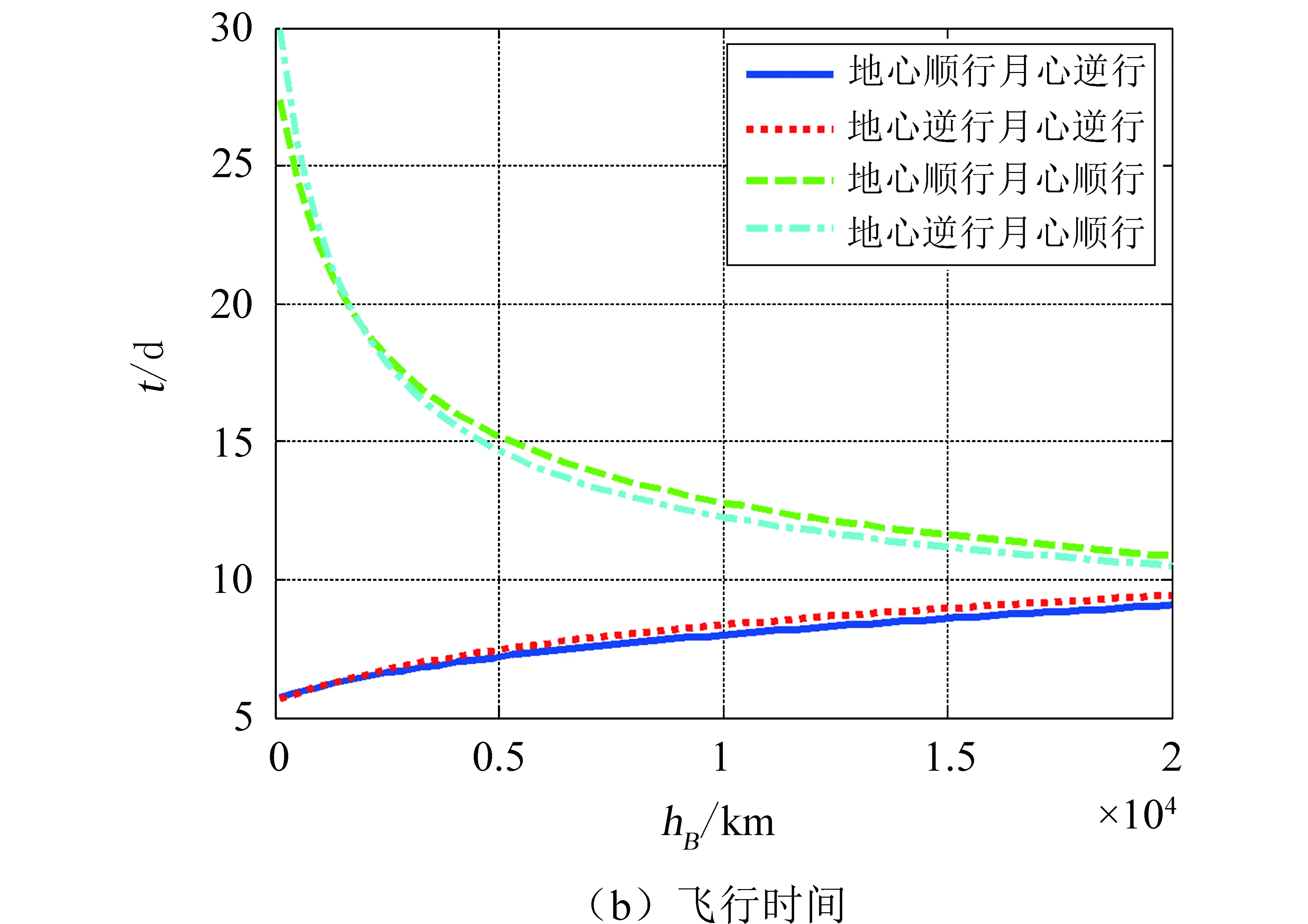
图8 对称自由返回轨道的速度增量和飞行时间随近地点高度变化曲线

4 结束语

本文针对载人月球探测任务和地月空间人员运输任务需求，基于圆型限制性三体模型提出了一种地月空间对称自由返回轨道设计方法。该方法收敛速度快，单次搜索时间仅为2 s左右；鲁棒性强，可适应近地点高度200～35 786 km和近月点高度100～20 000 km大范围变化的对称自由返回轨道求解；同时可搜索出指定地心和月心运行方向的自由返回轨道。利用该方法分析了不同近地点和近月点高度的自由返回轨道特性。结果表明：近地点高度主要影响地月转移入射速度增量，近地点高度越高，速度增量越小；近月点高度主要影响飞行时间，近月点高度越高，月心逆行轨道飞行时间越长，而月心顺行轨道飞行时间越短。

对于对称自由返回轨道，月心逆行轨道飞行时间约为6 d，明显低于月心顺行轨道约30 d的飞行时间，更适合载人飞行的时间约束。同时，地心顺行轨道所需地月转移入射速度增量小，可节省变轨推进剂消耗；且地心顺行轨道能有效利用地球自转速度，降低了对火箭运载能力的需求。因此，地心顺行月心逆行的自由返回轨道是地月空间人员运输轨道的最佳选择。