空间近场无线能量传输系统电磁屏蔽建模与仿真分析

朱立颖 马亮 张晓峰 刘治钢

(北京空间飞行器总体设计部，北京 100094)

无线能量传输技术是借助电磁场或者电磁波进行能量传输的一种技术[1]，一般分为电磁耦合式和微波(电磁辐射)2种，电磁耦合式根据传输原理不同又可分为感应耦合式和共振耦合式[2-3]。相对而言，微波传输距离较远，但其效率低，多应用于需要远距离无线传能的场合，如空间太阳能电站等。电磁耦合式传输距离在厘米级至米级，因此又被称为近场无线能量传输，具有传输效率高、易小型化、方向适应性强等优点，是有线能量传输方式不适用范围内的有效替代手段。无线能量传输系统是以交变的电磁场为空间介质进行能量传输。航天器对内部设备的体积、质量和电磁兼容等都有严格的要求，近场无线能量传输系统的应用首先要避免其对其余设备的影响。采用电磁屏蔽的方式可以减小近场无线能量传输系统对外部设备的影响，但电磁屏蔽体会改变近场无线能量传输系统的磁场分布，将对其磁场耦合特性产生影响，因此有必要开展电磁屏蔽对近场无线能量传输系统的影响分析。

近场无线能量传输技术在空间领域属于前沿技术，相关应用报道较少，可查到的如ESA拟在火星探测任务中的生物采样密封罐采用近场无线能量传输技术[4]。目前，对近场无线能量传输系统屏蔽前后周围磁场的解析研究也相对较少，通常使用软件仿真和试验测试对系统进行磁场分析。由于近场无线能量传输系统为高频电磁场环境，为讨论其周围磁场分布和建立仿真模型，主要通过交变磁场近似为准静态磁场来简化分析，但这与实际系统的磁场环境分布并非完全一致。在国内外对无线能量传输系统电磁屏蔽技术的研究中，文献[5]中使用Maxwell仿真软件对所设计的磁屏蔽无线能量传输系统进行仿真分析，分别研究了单线圈、加铁氧体进行屏蔽和加铁氧体与金属材料进行屏蔽3种情况下，线圈周围的磁场分布情况，并对线圈横向上的磁通密度进行分析。文献[6]中通过采用磁性材料改变磁场路径，利用金属导电板消除涡流，进而达到电磁屏蔽的目的，减小无线能量传输系统对器件的影响。文献[7]中使用Maxwell仿真软件对印刷电路板(PCB)式无线能量传输系统进行设计与分析。文献[8]中使用Comsol仿真软件对千瓦级电动汽车无线充电系统额定工作时在车体内及充电装置周围产生的电磁场进行分析，对比了收发装置整体屏蔽和其所提出的只在发射端外沿施加水平或竖直屏蔽3种屏蔽方式的屏蔽效果。上述文献均针对车辆应用近场无线能量传输技术的磁屏蔽特性开展仿真分析和试验研究，其特性与在空间应用的近场无线能量传输(包括输出功率、电压等级、传输距离等)不同，且未系统地开展电磁屏蔽对这些性能参数的影响分析。

基于近场无线能量传输系统在空间的应用需求，本文建立空间近场无线能量传输系统的电磁仿真模型，开展电磁屏蔽对其传输功率、工作电压等级、传输距离和工作频率的影响分析，解决交变电磁场环境下系统参数与屏蔽影响无法准确分析的问题，分析结果可用于空间近场无线能量传输系统增加电磁屏蔽后的系统参数设计。

1 空间近场无线能量传输系统特点及仿真模型

与传统的有线能量传输方式相比，空间近场无线能量传输技术具有无接插环节、无裸露导体、无漏电触电危险等优点，可满足空间在轨服务系统中在轨接管、在轨维修、在轨组装对能量传输的需求。同时，空间近场无线能量传输技术在无线配电、大功率太阳电池阵驱动机构、交会对接等方面具有重要的应用价值。

空间近场无线能量传输系统在航天器上应用时，会对航天器设备的电磁兼容性产生影响，应用屏蔽技术可以有效减小系统对外的电磁辐射影响，同时通过屏蔽措施可以提升本身系统的传输性能及抗干扰能力。因此，需要研究电磁屏蔽对空间近场无线能量传输系统的影响。①电磁屏蔽体使原设计的谐振补偿网络无法满足屏蔽后的系统需求，从而导致系统在非谐振状态下工作，为保证屏蔽后的系统工作在谐振状态，需要对系统的补偿网络进行重新设计。②由于屏蔽体为非线性磁材料，因此对屏蔽后系统周围磁场环境的理论推导较为复杂，很难得到准确的解析公式。③近场无线能量传输系统为高频电磁场环境，目前地面多采用将交变磁场近似为准静态磁场来简化分析，这与实际系统的磁场环境分布并非完全一致，若要得到更精确的系统周围磁场分布情况，需在交变电磁场环境下对系统进行分析。基于以上，本文利用Comsol仿真软件构建空间近场无线能量传输系统及其电磁屏蔽的仿真模型，选择场变量随时间变化的“瞬态”研究方法对模型进行设置和分析。空间近场无线能量传输系统模型包含线圈电磁模型(见图1)和电路传输模型(见图2)，通过瞬态耦合仿真实现对近场无线能量传输频域特性的分析。图1和图2中：IS为发射端电流；IL为接收端电流；L1和L2为发射和接收线圈在高频下的等效电感；M为线圈间的互感系数；C1和C2为串联的谐振电容；R1和R2为电路的等效电阻；Req为等效负载电阻；VS为发射端电压。

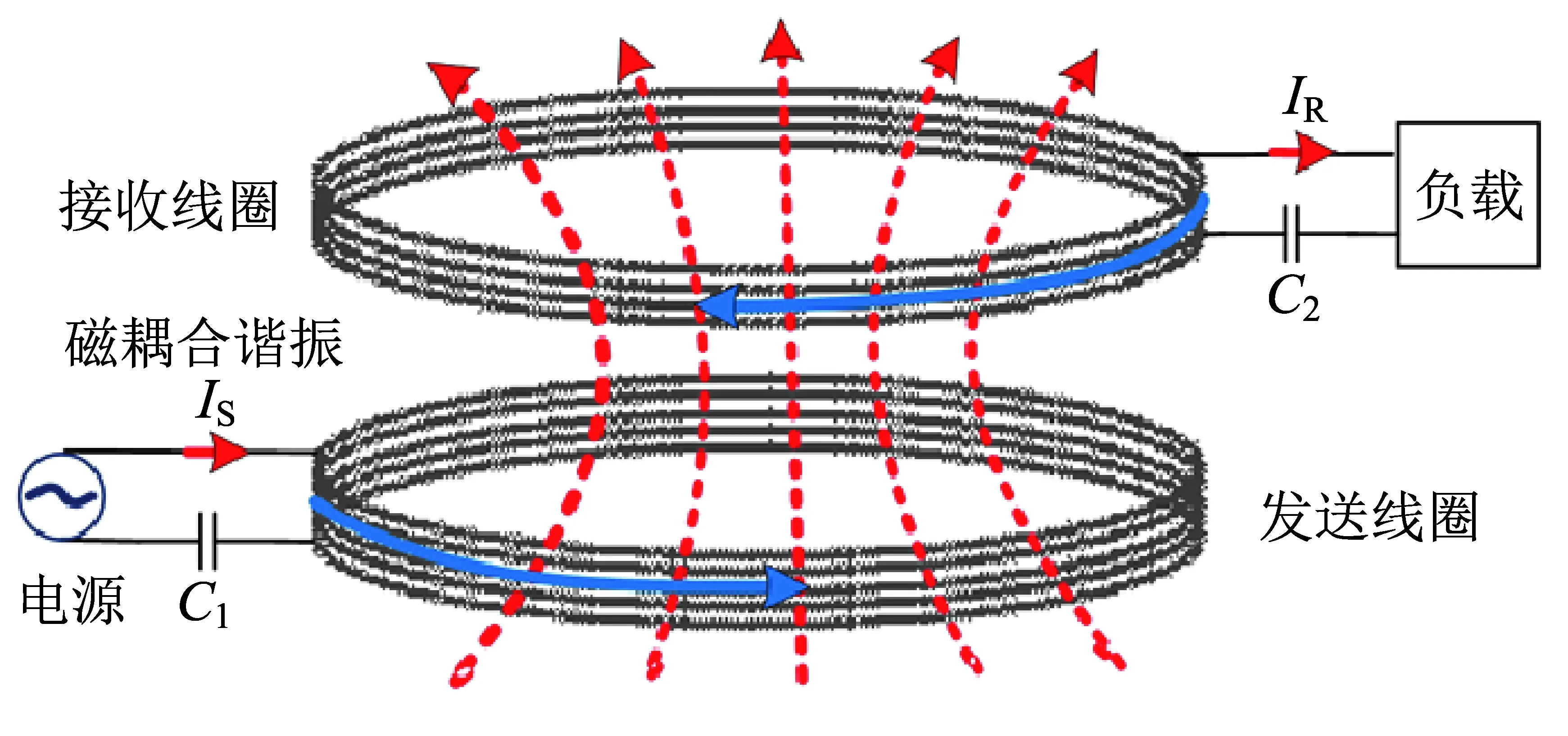
图1 线圈电磁模型Fig.1 Coil electromagnetic model

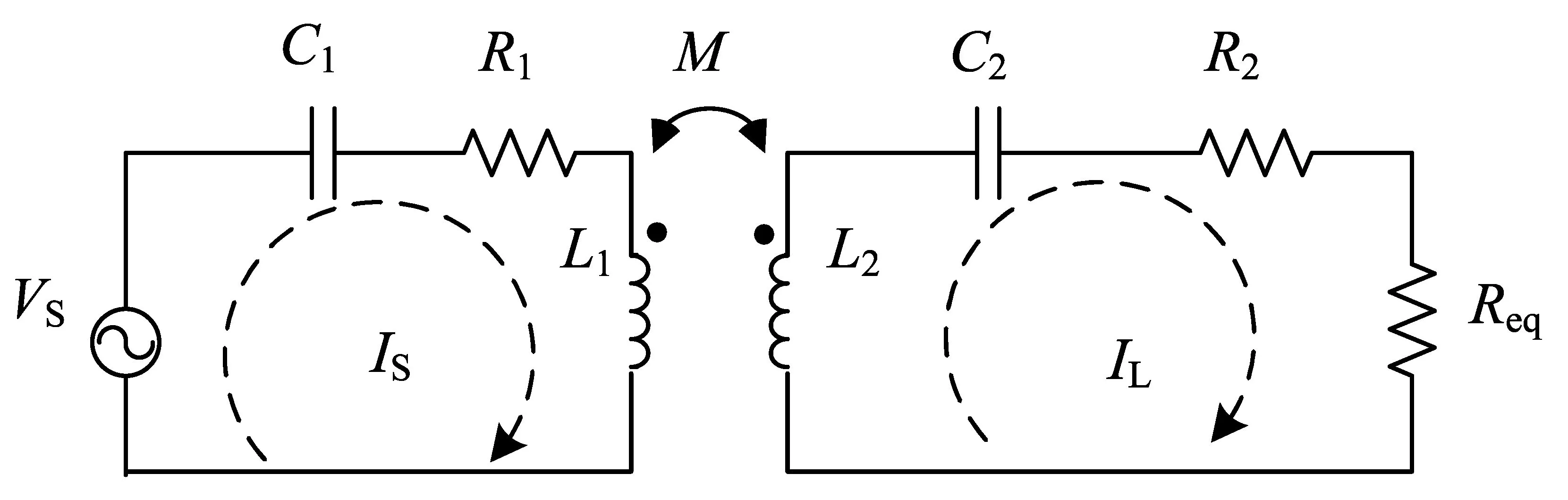
图2 电路传输模型Fig.2 Circuit transmission model

1.1 电路传输模型及计算方程

空间近场无线能量传输系统电路传输模型中，电路接口用于模拟系统中电流源、电阻、电容、电感等。此模型采用串串补偿的理想设计，输入阻抗角为零，系统效率最高。

根据基尔霍夫定律，列出发射线圈与接收线圈回路的电压方程，可求得电路各元件的参数。

(1)

式中：ω为角频率。

当电源频率等于系统谐振频率时，发生谐振，即

1/(jωC1)+jωL1=1/(jωC2)+jωL2=0

(2)

通过式(2)谐振条件，可对整个系统进一步求解，可得谐振角频率为

(3)

式中：f0为谐振频率。

可计算系统的负载电流幅值为

(4)

式中：PL为Req上的负载功率。

由此可知，当PL和Req确定后，可求得发射端电流IS的幅值为

(5)

通过式(3)～(5)，可大致计算出系统的各个参数。

由式(1)也可得到发射端电压与电流的关系为

(6)

当系统工作在谐振状态时，可得

(7)

(8)

系统的输出功率为

(9)

系统效率为

(10)

通常R1，R2远小于Req，因此式(10)可简化为

(11)

由式(11)可知，系统的工作频率、互感、负载电阻等对效率均有影响。

1.2 电磁屏蔽模型

为了简化设计，本文只用两线圈来设计系统。两线圈系统可用于模拟多线圈系统，对仿真分析结果无影响。无线能量传输系统中的线圈按结构可分为平面螺旋型线圈、圆柱螺旋型线圈、圆环同轴结构型线圈等，其中，平面螺旋线圈的耦合系数和品质因数都比较高，且集成度高、空间占用少，因此本文选用平面螺旋线圈。将平面螺旋线圈简化为同心圆并视为等效模型，这样，线圈模型在电路中既没丢失总电流，在电磁场计算中又能高效地对线圈模型进行有限元网格剖分和计算，且计算时所占计算机内存相对较少，可以提高计算速度。无线能量传输系统及其电磁屏蔽模型如图3所示。其物理场接口求解为Maxwell方程，对于线圈采用标量电势作为因变量。系统模型参数见表1，其中屏蔽体材料选用铁氧体材料，互感系数与线圈形状、周围磁性材料及线圈距离有关，由Comsol仿真软件直接计算得到。此系统模型主要对空间近场无线能量传输系统进行磁场仿真，磁场接口用于计算线圈、导体和磁铁内部和周围的磁场及感应电流分布，支持二维及三维的稳态、频域、小信号分析及时域模拟。

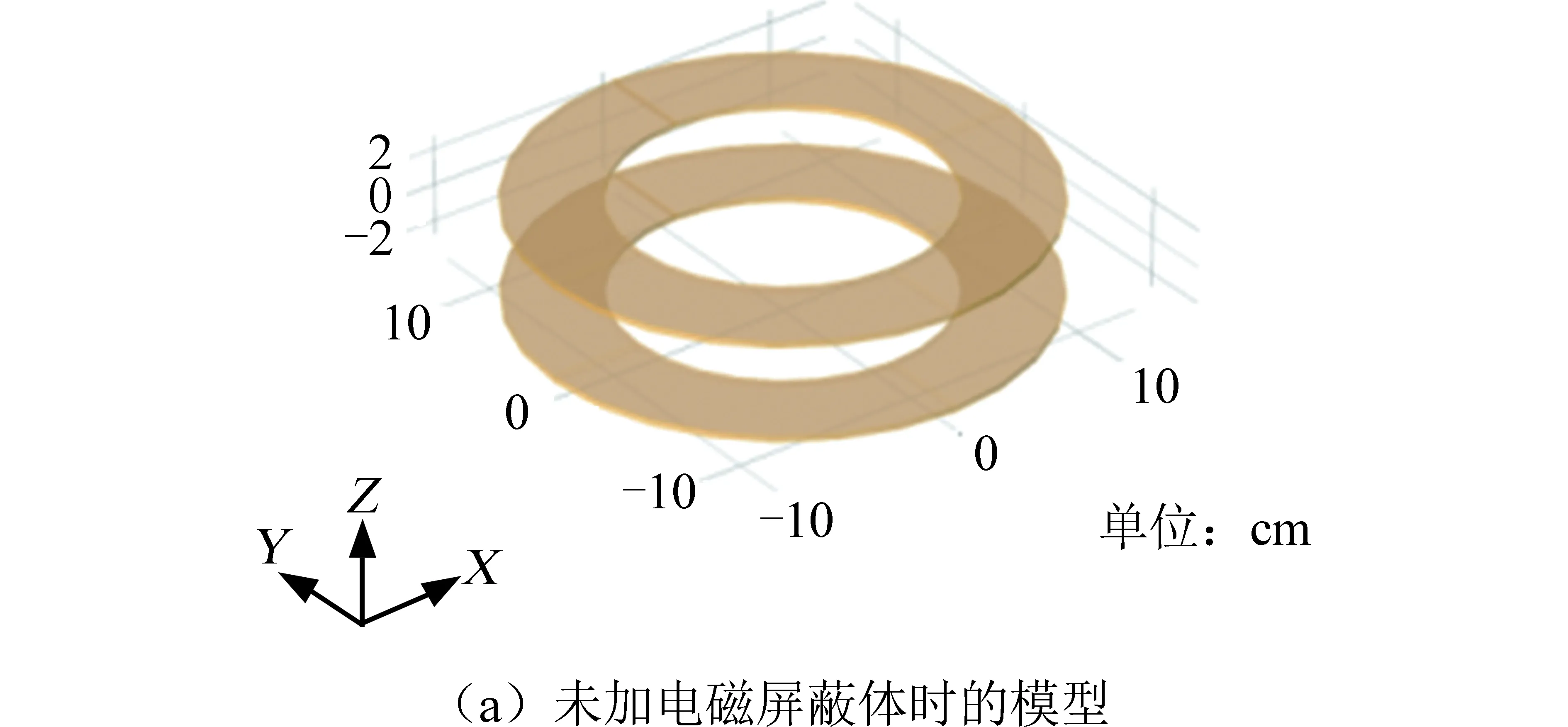
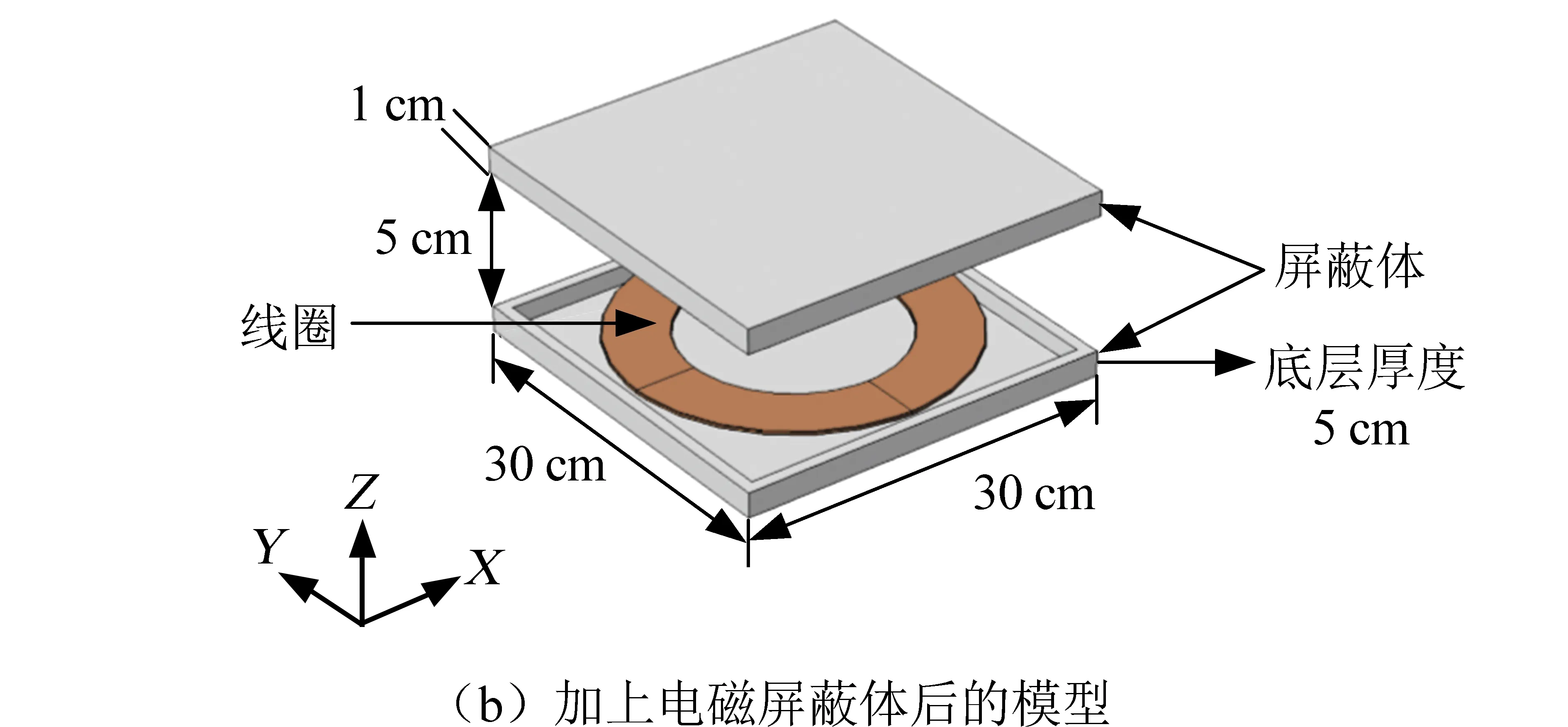
图3 电磁屏蔽模型Fig.3 Electromagnetic shielding model

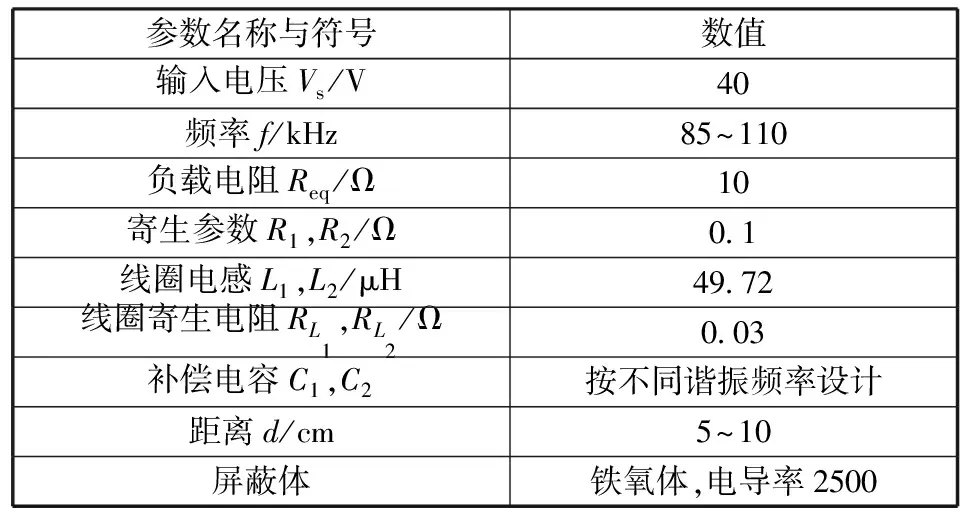
参数名称与符号数值输入电压Vs/V40频率f/kHz85～110负载电阻Req/Ω10寄生参数R1,R2/Ω0.1线圈电感L1,L2/μH49.72线圈寄生电阻RL1,RL2/Ω0.03补偿电容C1,C2按不同谐振频率设计距离d/cm5～10屏蔽体铁氧体,电导率2500

2 屏蔽性能仿真结果及分析

2.1 屏蔽下传输距离与系统效率关系

在研究屏蔽下传输距离与系统效率影响关系时，设定输入电压、工作频率、负载和线圈等不变，通过读取的线圈电感，并依据谐振条件计算出所需的补偿电容，仿真参数见表1，其中频率为100 kHz，补偿电容为50.85 nF。两线圈的距离变化范围为5～10 cm。

由图4可知，在系统加上铁氧体材料屏蔽体后，其整体效率高于不带屏蔽体时。这是因为：不带屏蔽体时，两线圈间的空间漏磁较多；带有屏蔽体后可有效减少空间漏磁，增大两线圈间的耦合系数。在屏蔽条件下，当线圈距离较近时，系统的整体效率较高；但随着两线圈的距离加大，系统的效率大幅下降。当两线圈间的距离为5 cm时，系统的效率可达94%；当距离变为10 cm时，系统的效率降为81.5%。这是因为两线圈距离变大后，它们之间的磁场耦合逐步减弱，相应耦合系数减小。

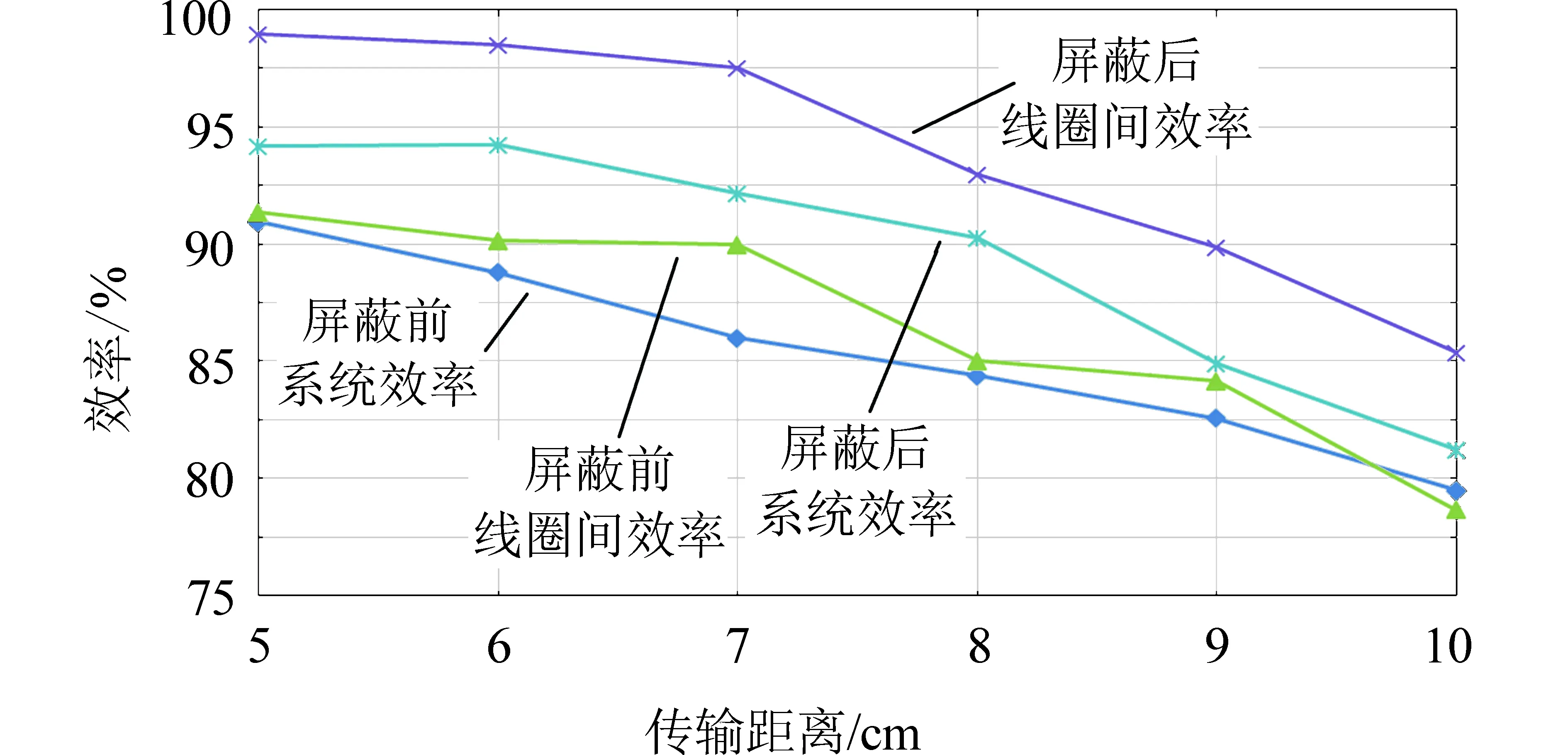
图4 传输距离与系统效率和线圈间效率的关系Fig.4 Gap length versus system efficiency and coil efficiency

由图5可知，未加屏蔽体时，系统的负载端的功率随着距离的变大而先增加后减小，这是由于两线圈距离很近时耦合系数较大，由式(7)和式(8)可知，在输入电压、补偿电容、寄生电阻和负载不变的情况下，系统接收端电流受互感的影响较大，接收端电流随互感的减小而变大。系统加上屏蔽体后，铁氧体屏蔽体增加了两线圈间的耦合，但是屏蔽体同时也对线圈的自感有很大的影响。在两线圈距离很近时，耦合机构间的磁场耦合较为紧密，所以加屏蔽体后线圈自身参数的变化对系统的影响较小；当距离变大后，由于耦合机构间的磁场耦合减弱，即系统的互感减小，由式(6)所示，在互感较小而线圈自感较大的情况下，系统输出端的电压与电流的相位差也会变大。

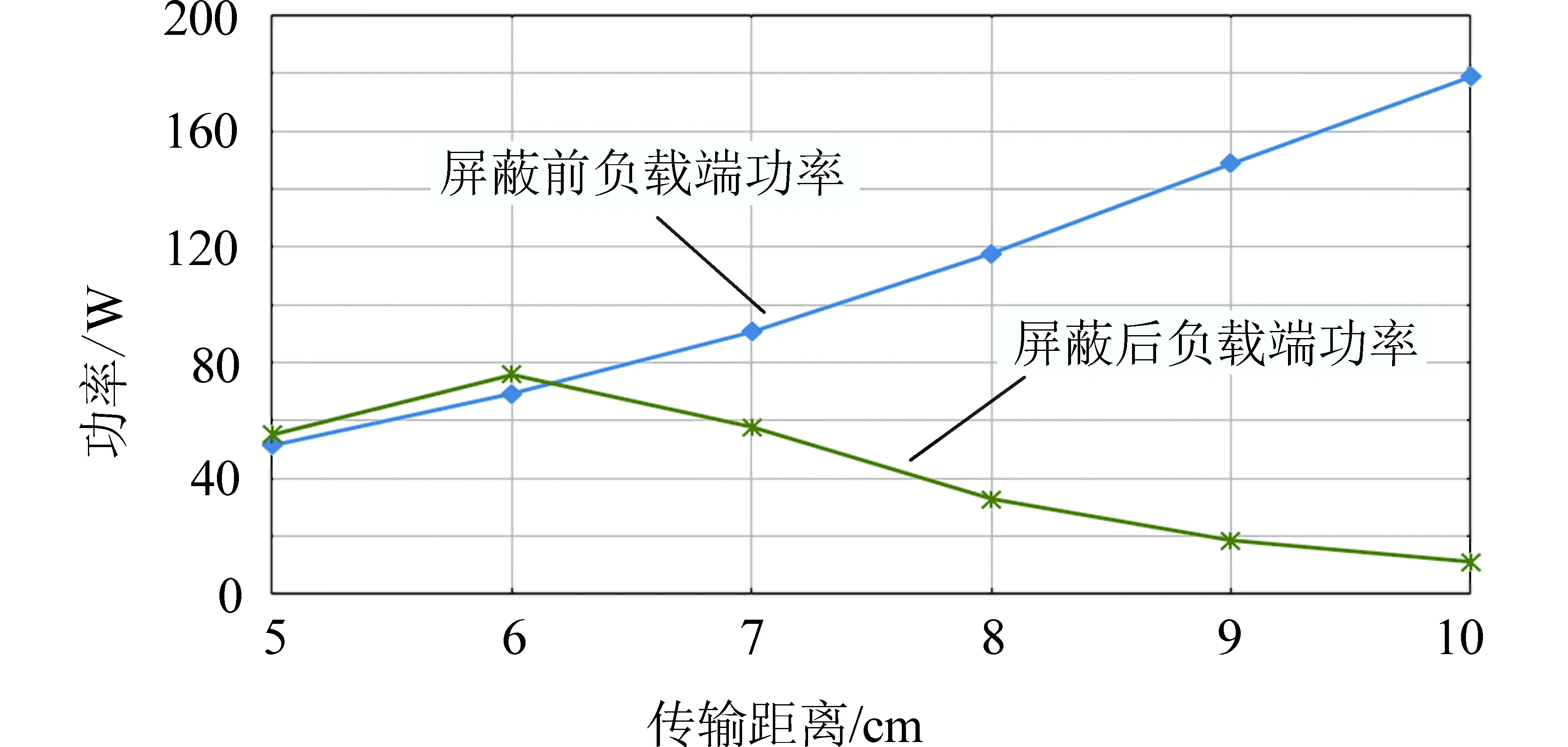
图5 传输距离与系统负载端功率的关系Fig.5 Gap length versus power of system load

由图6可知，通过使用屏蔽体对系统进行电磁屏蔽后，耦合磁场外侧垂直方向10 cm以外区域磁屏蔽效能均大于26 dB，随着两线圈距离的增加，屏蔽体对耦合磁场的屏蔽性能也有所提升。当两线圈距离较近时，线圈上流过的电流较小；随着距离的增加，耦合系统的影响减弱，导致线圈上的电流逐渐变大，随之在所测点的磁场强度也会变大。当系统加上屏蔽体后，在距离较近时屏蔽体对系统的影响较小，但随着距离的变大，屏蔽体的影响逐渐加大，系统的屏蔽效能也得到了进一步的提升。

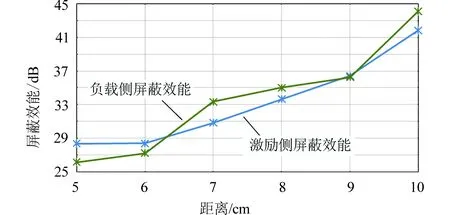
图6 传输距离与系统屏蔽效能的关系Fig.6 Gap length versus system shielding effectiveness

2.2 屏蔽下输入电压与系统效率关系

在仿真分析屏蔽条件下输入电压与系统效率的影响关系时，设定工作频率、补偿电容负载、线圈和线圈距离不变，各参数的值见表1，两线圈距离为5 cm。

输入电压对无线能量传输系统及其屏蔽性能的影响如图7所示。由图7可知：未带屏蔽体时，系统的整体效率和线圈间的效率都可达91%以上；带屏蔽体后，系统的整体效率可达94%，而线圈间的效率可高达95%以上。在其他参数不变的情况下，屏蔽后，输入电压的等级对系统的效率基本没有影响。

由图8可知，随着输入电压等级的增加，系统的输出功率以二次方增加。由式(7)和式(8)可知，在其他参数不变的情况下，接收端电流与输入电流成正比关系，同时由于负载为纯电阻，因此负载端的输出功率也随电压的增加以二次方关系增加。同理，在相同的电路参数条件下，带屏蔽体后的系统负载端的输出功率与输入电压成平方关系。

由图9可知，通过铁氧体对耦合系统进行屏蔽后，输入电压的等级对屏蔽后系统的屏蔽效能基本没有影响。使用屏蔽体后，屏蔽体对激励侧的屏蔽效能可达28.3 dB，对负载侧的屏蔽效能可以达26.2 dB，使用铁氧体对系统进行屏蔽基本可达到较好的屏蔽效能。

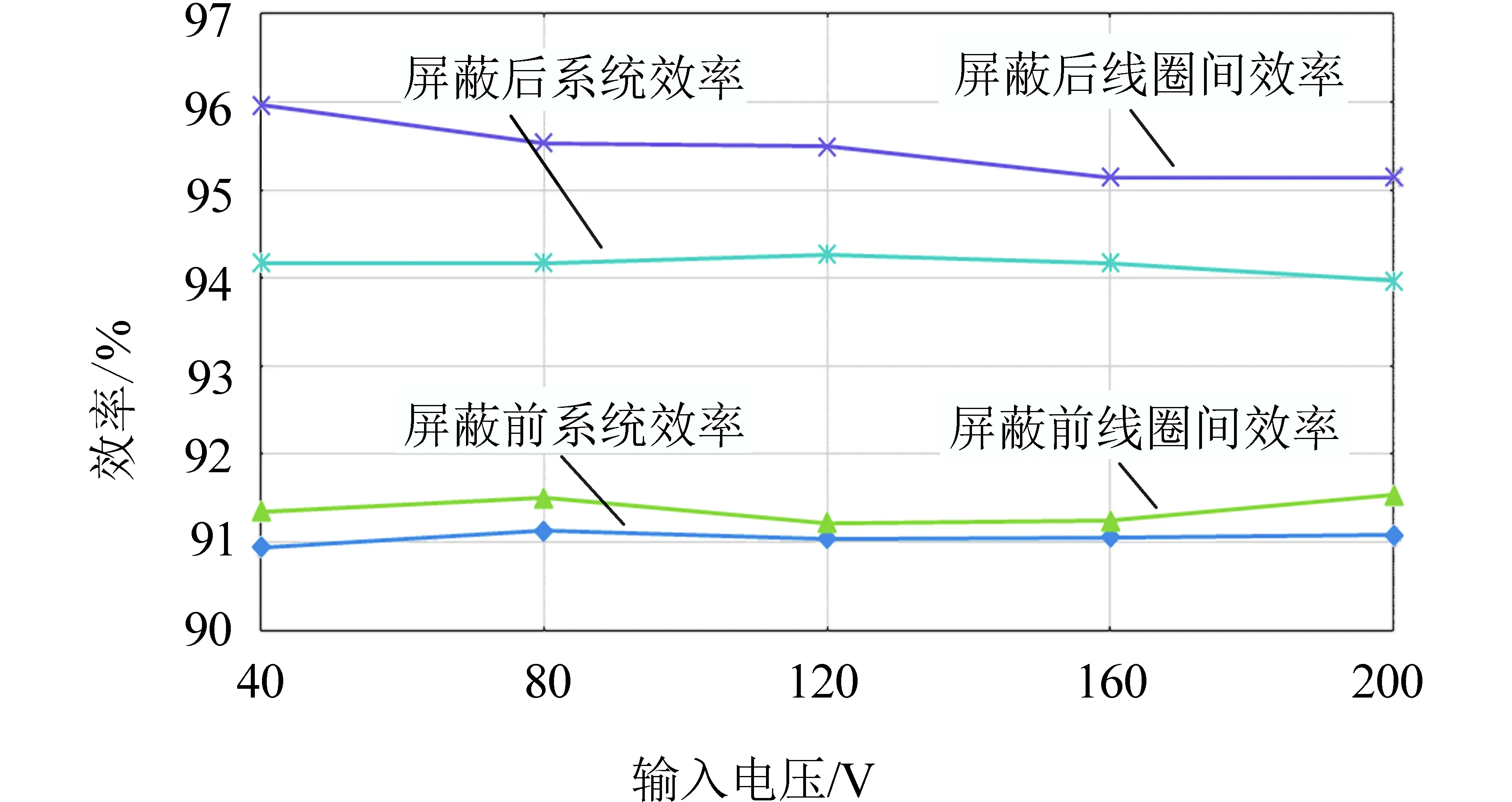
图7 输入电压与系统效率和线圈间效率的关系Fig.7 Input voltage versus system efficiency and coil efficiency

图8 输入电压与系统负载端功率的关系Fig.8 Input voltage versus power of system load

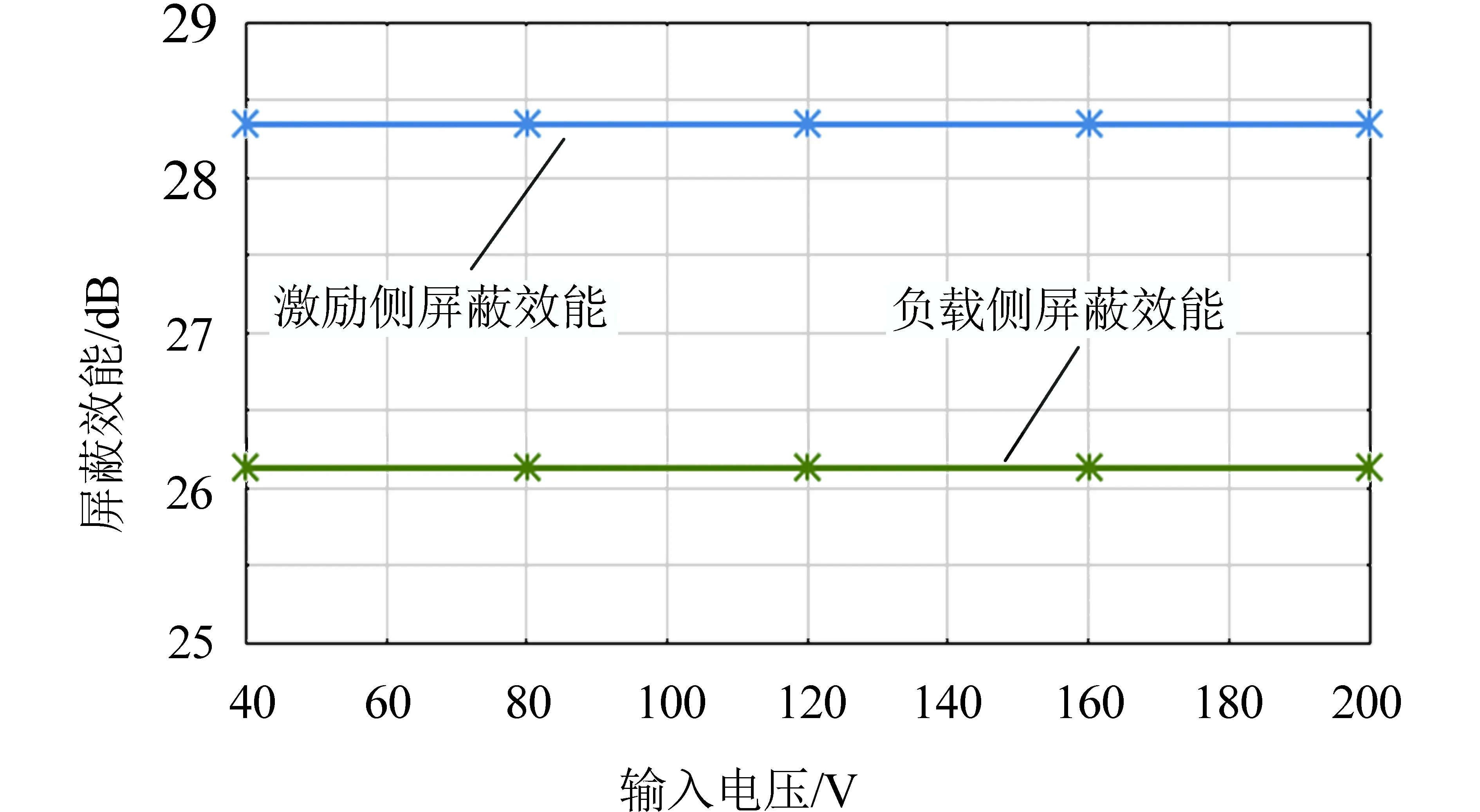
图9 输入电压与系统屏蔽效能的关系Fig.9 Input voltage versus system shielding effectiveness

2.3 屏蔽下负载与系统效率关系

在仿真分析输入负载对无线能量传输系统及其屏蔽性能的影响时，设定工作频率100 kHz、补偿电容50.85 nF、线圈距离5 cm，其余参数见表1。

输入负载对无线能量传输系统及其屏蔽性能的影响如图10所示。当输入负载电阻值较大时，未带屏蔽的系统效率较低。由式(6)和式(7)可知，假设负载电阻值很小，则两线圈间的互感对发射端电流的影响较大，这将使线圈间的电流减小，且对输入端的相位角影响较大。带屏蔽体后，负载对系统效率的影响较小，在负载电阻值由小变大时，系统的效率与线圈间的效率基本相近，变化较少，达到92%以上。由图11可知，未带屏蔽体时，系统负载端功率与负载电阻值成正比例关系。带上屏蔽体后，系统负载端功率在负载电阻值为2.5～10 Ω时，输出功率略高于未加屏蔽体，但随着阻值的变大，功率会有所减小。由图12可知，通过铁氧体对耦合系统进行屏蔽后，随着负载电阻值的变大，系统的屏蔽效能会有小幅的上升，在激励侧屏蔽效能基本在27.8 dB以上，而在负载侧的屏蔽效能偏低，负载电阻值小于10 Ω时，屏蔽效能略低于26 dB。

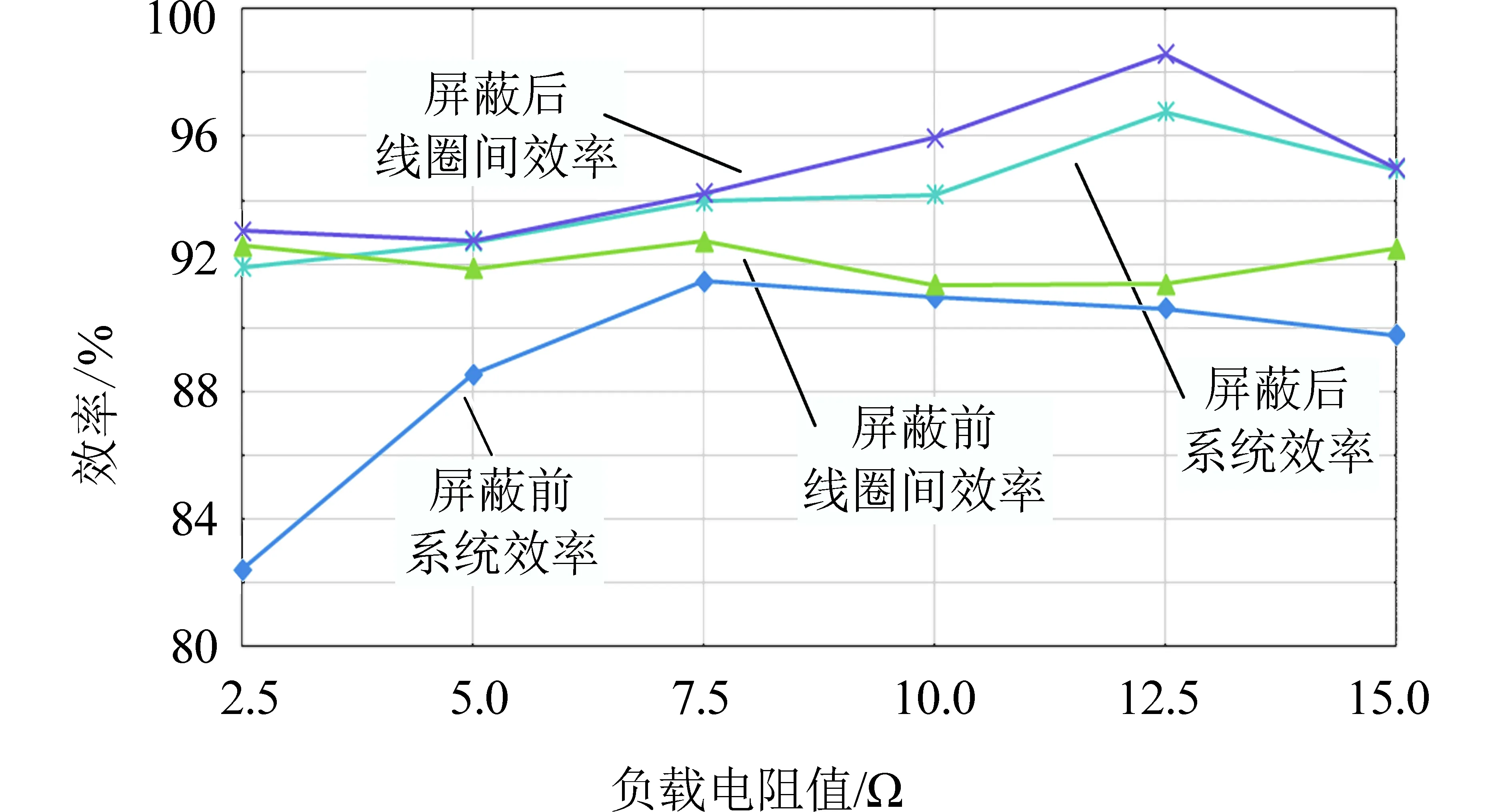
图10 负载电阻值与系统效率和线圈间效率的关系Fig.10 Load resistance versus system efficiencyand coil efficiency

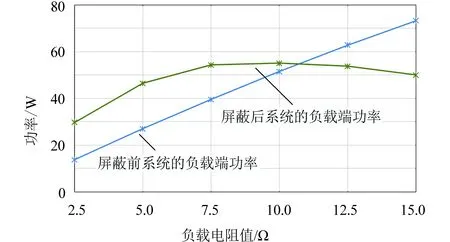
图11 负载电阻值与系统负载端功率的关系Fig.11 Load resistance versus power of system load

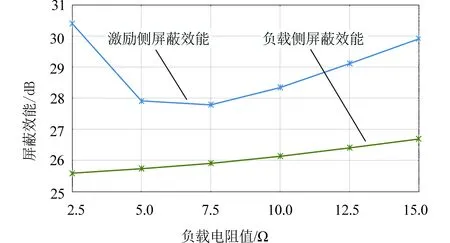
图12 负载电阻值与系统屏蔽效能的关系Fig.12 Load resistance versus system shielding effectiveness

2.4 屏蔽下频率与系统效率关系

在仿真分析频率对无线能量传输系统及其屏蔽性能的影响时，参数设置如表1所示。其中，设定两线圈距离为5 cm，已知线圈的自感，并依据谐振条件按照不同的工作频率计算所需的补偿电容，如表2所示。

表2 不同频率所对应的补偿电容值

仿真分析结果见图13。未带屏蔽体时，系统的效率随着频率的上升会有小幅的下降；带屏蔽体后，系统的效率也会随频率的上升有小幅的下降。但是，系统的整体效率不会随频率的变化而有很大的变动，带屏蔽体时，系统的整体效率可达94%～96%，两线圈间的磁场耦合在85～110 kHz的频率范围内基本不变。未加屏蔽体时，系统负载端的功率随着工作频率的变大而减小，如图14所示。由式(6)和式(7)可知，当激励电压和负载不变时，耦合机构两线圈的工作频率越小，发射端电流和接收端电流都会变大，导致系统的输出功率变大，这与理论分析一致。同理，带屏蔽体后，对整个系统而言，只改变了两线间的耦合关系，在其他条件不变的情况下，发射端电流和接收端电流会随着工作频率的减小而增加。由于系统的负载为纯电阻，因此功率的变化趋势与接收端电流相同。

由图15可知，通过铁氧体对耦合系统进行屏蔽后，工作频率对屏蔽后系统的屏蔽效能会有小幅的影响，随着工作频率的上升，铁氧体对系统的屏蔽效能会有所下降。带屏蔽体后，屏蔽体对激励侧的屏蔽效能可达28.5～29.0 dB，对负载侧的屏蔽效能可达26.0～26.3 dB。

需要说明的是，本文中仿真参数来源于目前空间应用近场无线能量传输系统样机，对于不同的工程电路，其参数不同，但基于电路传输模型(图2)及式(1)可知，本文的仿真结果对参数不同的工程电路具有参考价值，得到的变化趋势可用于指导近场无线能量传输系统的设计。另外，本文中铁氧体材料选择了常值电导率，铁氧体材料在实际应用中不完全线性，导致仿真结果存在误差。不过，铁氧体材料电导率增大或减小的幅度较小，其仿真结果趋势变化不大，因此可作为空间应用近场无线能量传输系统设计的参考。

图13 工作频率与系统效率和线圈间效率的关系Fig.13 Frequency versus system efficiency and coil efficiency

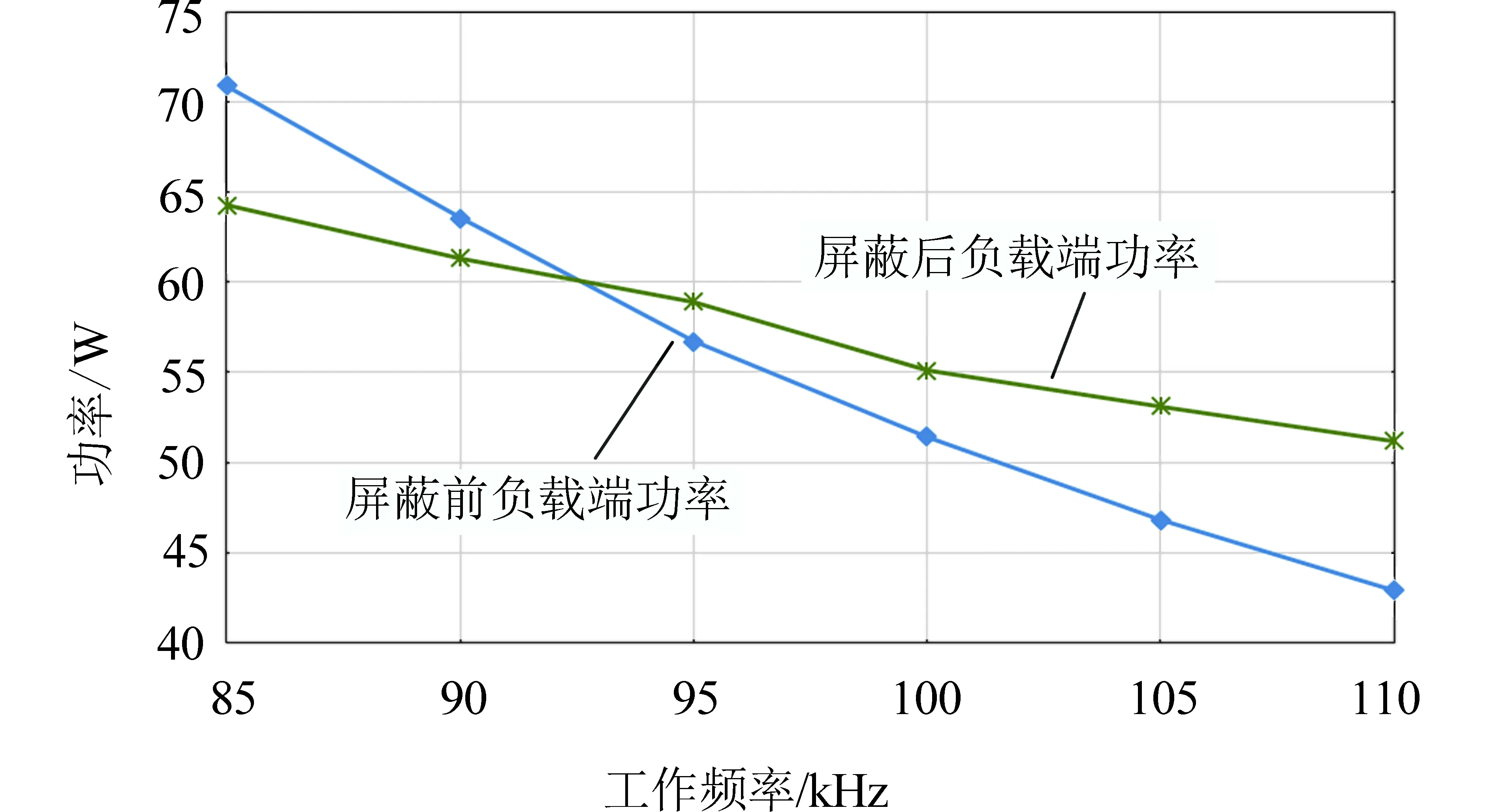
图14 工作频率与系统负载端功率的关系Fig.14 Frequency versus power of system load

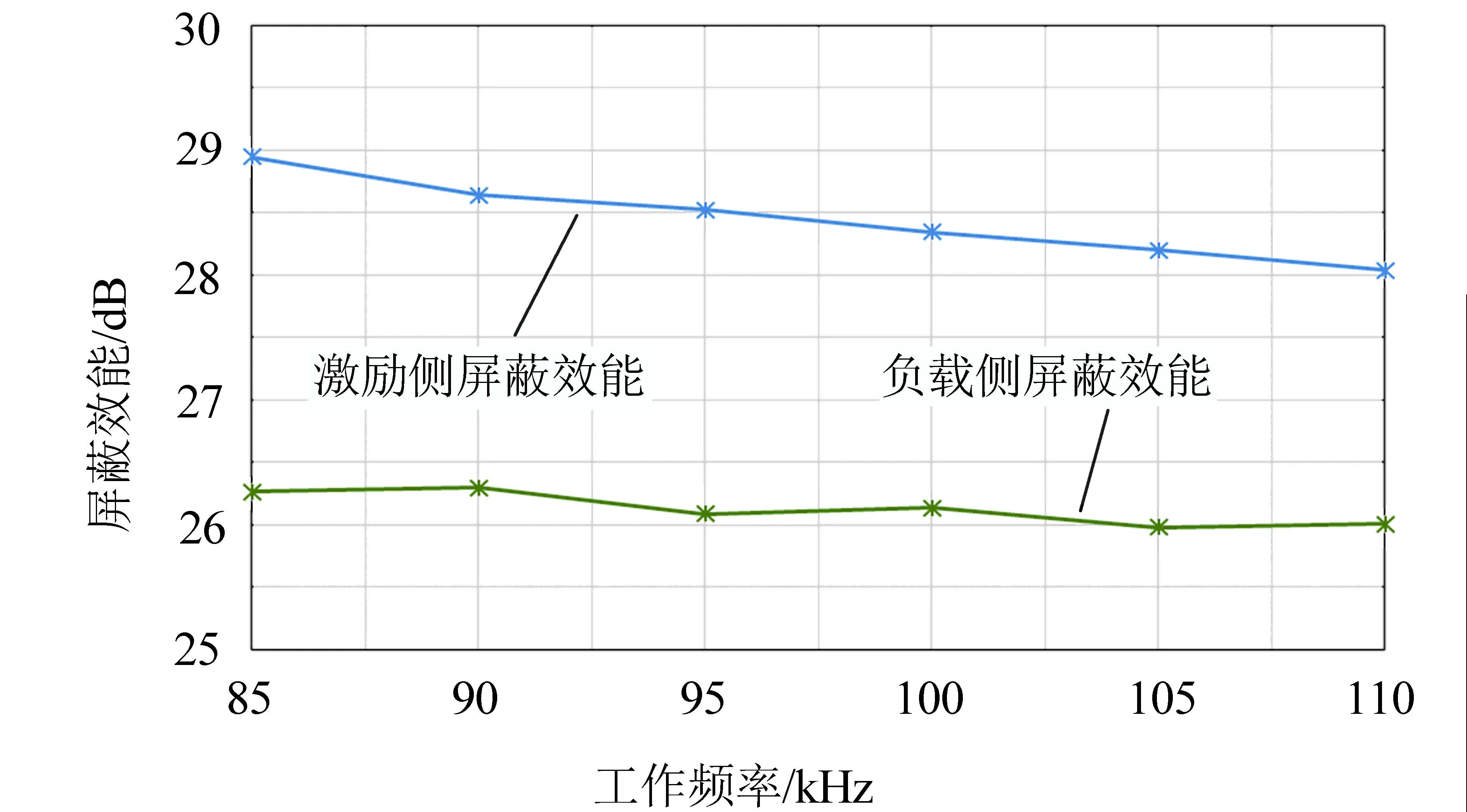
图15 工作频率与系统屏蔽效能的关系

3 结论

本文建立了瞬态感应耦合无线能量传输系统的电磁仿真模型，开展了电磁屏蔽条件下传输功率、工作电压等级、传输距离、工作频率对系统效率的仿真分析，得到结论如下。

(1)在电磁屏蔽体条件下，系统效率随着传输距离的增大而减小，在距离较近时屏蔽体对系统的影响较小，但随着距离的变大，屏蔽体的影响逐渐加大，系统的屏蔽效能也得到了进一步的提升。

(2)电磁屏蔽下，输入电压的上升会提升线圈上的电流，使线圈周围的磁场有所增大，但对屏蔽效能无太大影响。

(3)存在电磁屏蔽时，负载电阻对系统的效率影响较小，输出功率略高于未加屏蔽体时，但随着负载阻值的增大，输出功率会有所下降。通过铁氧体对耦合系统进行屏蔽后，随着负载阻值的增大，系统的屏蔽效能会有小幅的提升。

(4)在电磁屏蔽条件下，系统效率和屏蔽效能会随着工作频率的增加而有微幅的减小。

空间近场无线能量传输系统若采用直接加屏蔽体的方式，系统的效率与屏蔽效能等会有所提升，但系统的输出功率会大幅减小，系统中的无功成分会大幅增加。为了使屏蔽后的系统与未屏蔽的系统输出功率相近，在得到屏蔽体对线圈影响而增大的自感值后，可匹配相应的补偿电容，使系统工作在谐振状态，与此同时，输入端的电压也相应的加大。本文为空间近场无线能量传输系统增加电磁屏蔽后系统参数的选取及屏蔽效能的评估提供依据。目前，空间近场无线能量传输的传输距离低于1 m，对其应用存在限制。因此，除电磁兼容及电磁屏蔽外，还应针对谐振补偿网络、高效同步整流设计、线圈优化设计、空间环境适应性等开展相关研究。