基于Allee效应的麦蚜种群捕食-食饵模型的分析与控制
2019-01-10赵晓月赵立纯刘静娜
赵晓月,赵立纯,,刘静娜,王 欢
(1.辽宁师范大学 数学学院,辽宁大连 116029;2.鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)
群居有利于物种的生长和存活,但过分稀疏和过分拥挤都可阻碍其生长,从而对物种的生长繁殖产生副作用,每一物种都有自己最适宜的密度,这就是所谓的Allee效应[1].植物、哺乳动物、海洋无脊椎动物等产生Allee效应现象,该现象一直是生态学和保护生物学的一个研究热点.近年来,具有Allee效应的物种捕食模型被广泛研究.魏雪莹等人研究了麦蚜种群模型的突变控制,利用控制器使麦蚜种群的数量下降[2].李文霞、许洪建等人建立了食饵含Allee效应的最优捕获模型,利用Pontryain最大值原理确定了最优捕获策略[3].付晓阅、刘超等人建立了具有Allee效应的食饵-捕食模型,分析了各平衡点的局部渐近稳定性,通过构造Lyapunov函数分析了平衡点的全局渐近稳定性[4].上述文章从理论上对具有Allee效应的捕食-食饵模型进行分析和研究,而在麦蚜生态系统的应用很少见.因此本文将具有Allee效应的麦蚜种群作为食饵得到麦蚜种群的捕食模型,借助微分方程定性理论和Hopf分岔理论[5,6],对平衡点的稳定性进行分析,然后通过状态反馈控制消除Hopf分岔抑制了麦蚜种群的突变现象.
1 模型建立
考虑具有Allee效应的logistic模型[7]
(1)
其中,x为种群密度,r为种群的内禀增长率,K为其环境容纳量,A为其阈值密度.
(2)
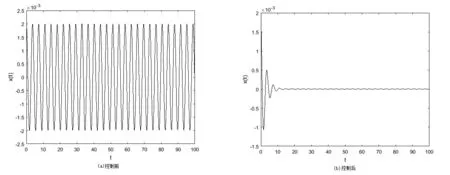
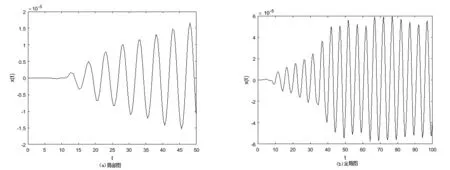
其中,0 食饵-捕食模型中,食饵种群可能受自身繁殖或被捕食者的影响而具有Allee效应.当食饵种群具有Allee效应时,食饵-捕食模型可能失去稳定性而产生突变现象.由于麦蚜种群会产生突变现象从而可以用Allee效应刻画麦蚜种群的增长.在logistic模型[8]的基础上得到模型如下: (3) 设y(t)表示t时刻麦蚜天敌种群的密度,d为麦蚜天敌种群的死亡率,结合模型(3)得麦蚜种群食饵-捕食模型 (4) 其中,b是天敌种群的捕食率,c是转化系数,a,b,c,d均为正数. 转化系数c在麦蚜种群中起着重要作用,因此视其为模型(4)中Hopf分岔分析的主要参数.随后对模型(4)进行定性分析. 为了方便起见,令 f(x,y)=x[a(k-x)(x-k0)]-bxy,g(x,y)=cxy-dy, 则模型(4)变为 (5) 下面讨论各个平衡点的稳定性: 相应的特征方程为 特征根为 且 (6) 对模型(6),如果自然界中的天敌种群不能达到调节麦蚜种群密度的目的,可以通过人工捕获麦蚜的方式控制麦蚜种群密度.相应的控制模型如下: (7) 其中,k1是人工捕获麦蚜种群的捕获效率. 相应的特征根为 根据Hopf分岔理论,得如下定理1. 从而可得 (8) 根据式(8)可知,随着捕食效率k1的增大,模型(7)的转化数c将增大,即Hopf分岔的临界点将延后,由于转化系数c的改变使得麦蚜种群的增长速度渐缓,即使有Hopf分岔引起的突变现象发生,但其发生的时间延迟.综合上述得如下定理2. 定理2对模型(7),如果控制 对定理1,取k0=100,k=2 900,a=0.000 01,b=7,c=0.000 1,d=0.15,得状态反馈控制增益k1=0.8,其时间响应图见图1. 图1 定理1 中模型控制前后时间响应图 比较图1中的两图可以看出,通过人工捕获不仅消除麦蚜的突变现象,而且使麦蚜生态系统中的麦蚜种群数量保持在不损害作物的水平. 对定理2,取k0=100,k=2 900,a=0.000 01,b=5,c=0.000 2,d=0.3,得状态反馈控制增益k1=7.2,其相应的时间响应图见图2,图3. 图3 定理2中模型控制后时间响应图 比较图2和图3的局部图,对于控制前的麦蚜生态系统,在t≈5时蚜虫种群开始出现Hopf分岔导致的突变现象;对于控制后的麦蚜生态系统,在t≈10时蚜虫种群开始出现Hopf分岔导致的突变现象.这说明通过人工捕获可以使突变现象发生延迟,这对于处在灌浆期的麦田生态系统有着重要的意义. 本文采用两种控制方法,使麦蚜种群的突变现象消失.由仿真结果可知定理1的控制效果比定理2的控制效果好,但是在具体实施的过程中外界因素可能会对控制产生影响,所以要根据具体情况采用不同的方法进行控制.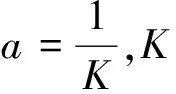
2 模型分析
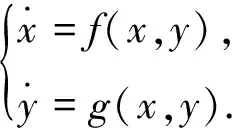
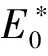
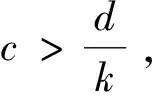
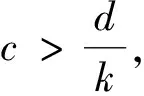
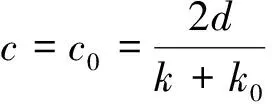
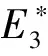
3 控制器设计
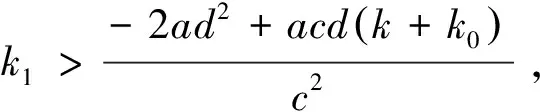
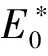
4 数值仿真