复合材料层合板自由振动分析的无网格自然邻接点Petrov-Galerkin法

陈莘莘， 李 鹤

（华东交通大学 土木建筑学院，南昌330013）

1 引 言

复合材料层合板［1］在工程实际中的应用日益增多，对其进行自由振动分析一直是计算固体力学研究的重要课题之一。相对于经典层合板理论，一阶剪切变形理论［2］能更好地描述板的横向剪切变形，从而在板壳结构分析中得到了广泛的应用。

随着电子计算机的广泛应用，有限元法在复合材料层合板的分析问题中得到了广泛的应用［3，4］。但有限元法分析复杂结构在前处理时的网格划分工作量巨大。为了摆脱网格的束缚，近年来发展迅速的无网格法［5，6］不需要在求解域内划分用于确定插值函数的单元网格，引起了国际计算力学界的高度重视。目前具有代表性的无网格方法主要有无单元 Galerkin法［7，8］、自然单元法［9，10］、无网格局部 Petrov－Galerkin 法［11，12］和 重 构 核 粒 子 法［13，14］等。其中，无网格局部 MLPG（Petrov-Galerkin）法是一种比较流行的无网格方法，这种方法允许试函数和权函数取自不同的函数空间，并且不需要用于数值积分的背景网格，是一种真正的无网格法。但是，由于移动最小二乘近似形函数不满足插值性质，这种无网格方法在施加本质边界条件时必须进行特殊处理。无网格自然邻接点Petrov-Galerkin法［15，16］是近年来提出的一种基于自然邻接点插值的MLPG方法，不仅具有自然单元法易于施加本质边界条件的优点，而且还融合了MLPG法的一些优良特性。该方法借助成熟的Delaunay三角化，不论对区域内部节点还是边界节点都可以简单快速地构造出多边形子域。目前，该方法在很多领域得到了广泛的应用［17－19］。

鉴于无网格法的优越性，许多学者［20－23］都致力于无网格法分析复合材料层合板的静力和动力问题，但是基于无网格自然邻接点Petrov-Galerkin法的复合材料层合板振动问题尚未见报道。本文采用局部加权余量法详细推导了无网格自然邻接点Petrov-Galerkin法在复合材料层合板自由振动分析中的理论公式，并给出了相应的数值实现过程。最后，通过数值算例验证了本文方法应用于复合材料层合板自由振动分析的有效性和合理性。

2 自然邻接点插值

考虑平面区域上的一组离散节点，其集合为N＝｛x1，x2，…，xM｝。对任一节点xI，其一阶 Voronoi结构可定义为

式中d（x，xI）为点x与节点xI之间的距离。显然，每个TI表示的是以节点xI为最近离散节点的空间点位置的集合。

在一阶Voronoi结构内，插值一个任意点x，把平面重新划分为二阶Voronoi结构TIJ。在每一个二阶Voronoi结构TIJ中，节点xI为最近邻接点，节点xJ为次近邻接点，用数学语言表达为

从几何上讲，TIJ实际是以节点xI为最近点，节点xJ为次近点的空间点位置集合。二维平面节点数n＝7的一阶Voronoi结构和待插点x的二阶Voronoi结构如图1所示。

根据Sibson插值的定义［9］，形函数I（x）的计算公式为

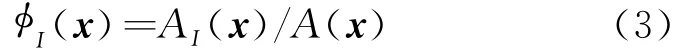
式中 AI（x）为二阶Voronoi结构TxI的面积，A（x）为一阶Voronoi结构Tx的面积。

定义了各节点的插值函数后，点x的位移函数可以表达为

式中 uI（I＝1，2，…，n）是点x周围n个自然邻接点的节点位移，I（x）为对应节点的形函数。

3 复合材料层合板的基本方程

如图2所示，厚度为h的纤维增强复合材料层合板，其中面与x-y坐标面重合。基于一阶剪切变形理论，板内任一点的三个位移分量可表示为

式中u0，v0和w0分别为中面 （z＝0）沿x，y和z轴方向的位移，θx和θy分别是横向法线变形后在xz平面和yz平面上的转角。

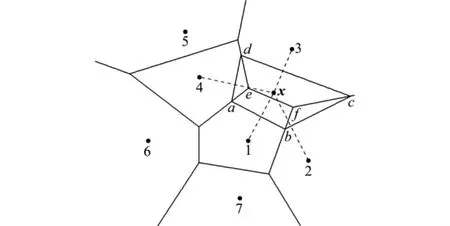
图1 任意点x的二阶Voronoi结构Fig.1 Second-order Voronoi cell about x

小变形条件下，板的应变ε＝［εxεyγxy］T可由式（5）表示为

横向剪切应变矢量γ＝［γxzγyz］T为

式中εm，κ和γ分别为薄膜应变、曲率和切应变。

复合材料层合板的广义内力为

式中

对于无阻尼自由振动问题，基于一阶剪切变形理论的复合材料层合板控制方程为［2］

4 离散方程的导出

将复合材料层合板的中面用N个节点离散，则平衡方程（17～19）的局部弱形式可以表达为

图2 复合材料层合板Fig.2 Sketch map of laminated composite plate

利用散度定理，方程（20a）可变为

如图3所示，无网格自然邻接点Petrov-Galerkin法的子域ΩIs是由围绕节点I的Delaunay三角形TIi构成。在每个Delaunay三角形TIi中，采用有限元的三角形线性单元形函数NI作为权函数，则无阻尼自由振动问题式（21）可以简化为

同理，对无阻尼自由振动问题式（20b，20c）可以简化为

为便于进行数值计算，把方程（22～24）改写成矩阵形式，有

式中

图3 局部多边形子域Fig.3 Local polygonal sub-domains

由于只对空间域进行离散，求解域Ω内任一点x处的位移u0＝［u0v0w0θxθy］T可由式（4）表示为

式中

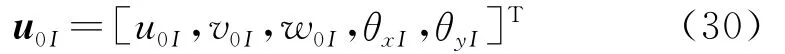
将式（29）代入式（25～27），可得复合材料层合板自由振动分析的离散控制方程为

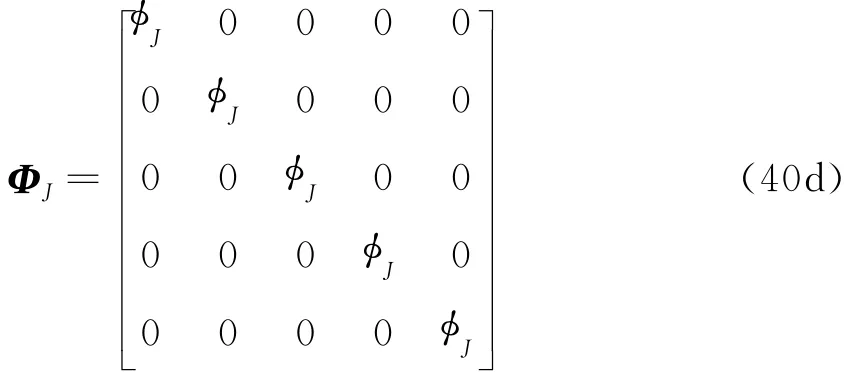
式中 U ＝［uT01， uT02，…，uT0N］T，K 和 M 分别为整体刚度矩阵和质量矩阵，可具体表示为

式中

方程（31）的解可以假设为

式中ω为振动频率，U为振型函数，t为时间变量，t0为初始时间。将式（41）代入式（31）可得

式（42）若要有非零解，则其系数矩阵行列式必须为0，即det（K－ω2M）＝0，其特征值和特征向量分别对应复合材料层合板的固有频率ω和振型向量U。

5 数值算例

为了验证本文的无网格自然邻接点Petrov-Galerkin法进行复合材料层合板自由振动分析的有效性，对两个典型算例进行了计算和对比分析。假设复合材料层合板每层厚度相同，且由均匀线弹性复合材料构成。剪切修正因子取为α＝π2／12，材料参数取为E1／E2＝（10，20，30，40），G12＝G13＝0.6E2，G23＝0.5E2，v12＝0.25，ρ＝1。矩形复合材料层合板常见的边界条件如下。

垂直于x轴的简支边：u0＝w0＝θy＝0

垂直于y轴的简支边：v0＝w0＝θx＝0

固支边：u0＝v0＝w0＝θx＝θy＝0

5.1 四层复合材料层合方板

考虑边长a＝1.0m，厚度h＝0.2m的四边简支对称复合材料层合方板（0／90／90／0）。为了研究收敛性，在计算时分别采用了17×17，19×19和21×21三种规则的节点布置方案。弹性模量比变化时的无量纲固有频率 （ω＝（ωa2／h））计算结果列于表1。为了进行对比，表1还给出了文献［2］的精确解。由表1可知，采用无网格自然邻接点Petrov-Galerkin法时，各种节点布置方案均有较高的计算精度，证明了本文方法的有效性。

5.2 三层复合材料层合方板

为了进一步考察本文方法的适应性，考虑边长a＝1.0m，厚度为h，弹性模量比为E1／E2＝40的三层对称正交复合材料层合方板（0／90／0）。采用25×25节点分布对不同厚跨比h／a的方板在四边简支（SS）、四边固支（CC）和两对边简支、另两对边固支（SC）边界条件下进行数值计算。前三阶无量纲化频率＝（ωa2／π2），计算结果列入表2，其中D0＝E2h3／12（1－v12v21）。为了进行对比，表2还给出了文献［24］的计算结果。由表2可知，两种不同方法所得结果吻合较好，进一步验证了本文方法的有效性。

表1 四层复合材料层合板的固有频率（ω）Tab.1 Fundamental frequency（ω）of the 4-layer laminated composite plates

表2 三层复合材料层合板的前三阶无量纲化频率）Tab.2 First three dimensionless frequency）of the 3-layer laminated composite plates

表2 三层复合材料层合板的前三阶无量纲化频率）Tab.2 First three dimensionless frequency）of the 3-layer laminated composite plates

B.C. h／a模态1 2 3 0.05 SS 0.1 0.2 Liew［24］ 6.138 8.888 15.110 Present 6.144 9.006 15.558 Liew［24］ 5.166 7.757 12.915 Present 5.129 7.802 12.844 Liew［24］ 3.594 5.769 7.397 Present 3.544 5.811 7.245 0.05 CC 0.1 0.2 Liew［24］ 10.953 14.028 20.388 Present 10.886 14.153 20.975 Liew［24］ 7.411 10.393 13.913 Present 7.310 10.451 13.669 Liew［24］ 4.447 6.642 7.700 Present 4.401 6.722 7.562 0.05 SC 0.1 0.2 Liew［24］ 6.890 11.246 18.664 Present 6.932 11.491 19.356 Liew［24］ 5.871 9.454 13.340 Present 5.860 9.590 13.152 Liew［24］ 4.137 6.474 7.664 Present 4.120 6.576 7.532

6 结 论

无网格自然邻接点Petrov-Galerkin法是一种计算公式简便、计算精度和计算效率均十分优良的数值方法。这种方法不仅充分发挥了无网格局部Petrov-Galerkin法的优点，而且形函数的计算不涉及矩阵求逆，更没有人为参数的选择问题。

基于一阶剪切变形理论，本文首次详细推导了无网格自然邻接点Petrov-Galerkin法应用于复合材料层合板自由振动分析的计算公式，并编制了相应的计算程序。算例分析表明，无网格自然邻接点Petrov-Galerkin法是复合材料层合板自由振动分析的一种有效可行的方法，具有计算精度高和前处理简单等优点。