机器学习FPGA硬件实验设计
2019-01-09汤知日
汤知日, 常 胜
(武汉大学 物理科学与技术学院微电子系, 物理国家级实验教学示范中心, 湖北 武汉 430072)
神经网络是机器学习的重要内容[1],也是科学研究的热点。出于科研和实际工程应用的需要和硬件计算方式与神经网络并行化本质的契合[2],在硬件电路平台实现神经网络已逐渐成为技术发展趋势之一。FPGA具有的可重用性和操作方便简单等优势,因而成为一种进行硬件实验实现神经网络的理想方式[3]。
目前还鲜有将“神经网络硬件化”作为实验教学内容。本文提出的实验,首先对神经网络的基本结构在算法级进行熟悉,再进一步在FPGA上实现图像分类的并完成设计性能的优化。通过此实验,既可培养学生对神经网络的理解和对FPGA数字集成设计技术[4]的掌握,也有望提升学生分析和解决复杂问题的能力及团队协作的精神。
1 神经网络概念及算法设计
1.1 神经元模型和算法架构
神经网络是通过对人脑的基本单元——神经元的建模和连接,探索模拟人脑神经系统的功能模型,并在此基础上提出的具有学习、联想、记忆和模式识别等智能信息处理功能的人工系统[5]。神经网络的一个重要特性是它能从环境中学习,并把学习的结果分布存储于网络的突触连接中。神经网络的学习是一个过程,在其所处环境的激励下,相继给网络输入一些样本模式,并按照一定的规则(学习算法)调整网络各层的权值矩阵,待网络各层权值都收敛到一定值[6],学习过程结束。之后,就可使用训练完成的神经网络来对真实数据进行分类。
作为实验的第一部分,让学生对神经网络基本概念有所了解。神经元基本结构如图1所示。
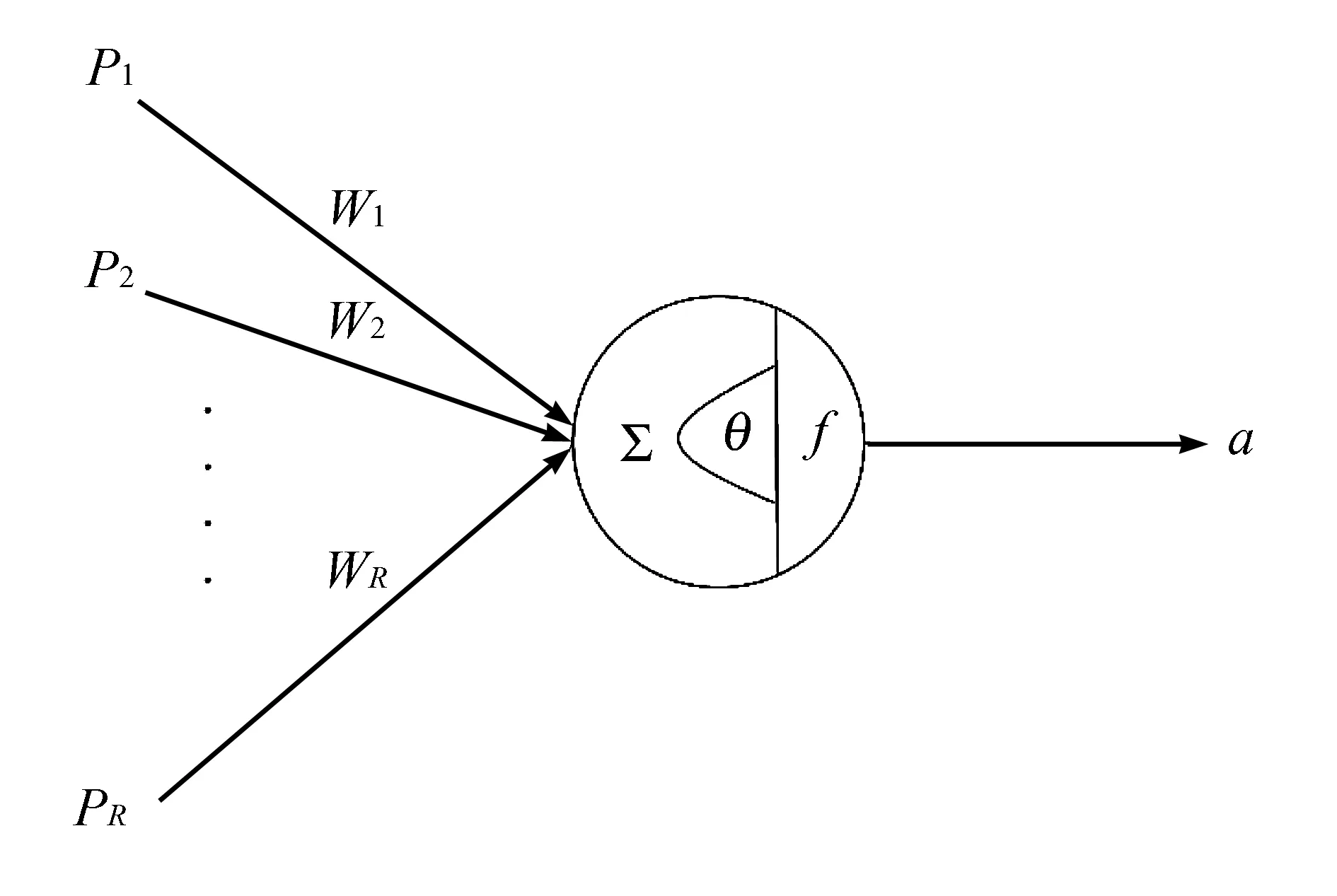
图1 神经元基本结构建模
根据图1可得:

其中b=-θ。PR为前端其他神经元的轴突输出,即此神经元的输入向量,WR为神经元连接的强度,其值可正可负。通过在误差反向传播的过程中修改这个强度值的大小,可模拟生物神经元中存在的兴奋和抑制兴奋两种神经递质。当输入向量和权值乘积之和大于某一阈值时,该神经元启动。f即为神经元之间的传递函数,也被称为激发函数或触发函数。
实验中训练和测试采用的数据集为3×3像素的二值字母图像,一共分为3类,如图2(a)所示。考虑到对网络容错率的分析,采用图2(b)中的30个图像对已完成训练的网络进行测试。

图2 3×3像素二值字母图像
1.2 神经网络算法设计
采用Matlab作为算法设计平台,使用其函数工具箱提供的newff函数来创建网络。具体调用格式为:
net=newff(P,T, [S1 S2…S(N-1)]),…
…{TF1 TF2…TFNI}
其中P和T分别为输入样本和期望响应,Si为网络各层的神经元数目,TFi为网络各层的传递函数类型。
利用此函数创建一个经典的误差反向传播(BP)神经网络,完成字母的图像识别。网络的建立和训练过程如下:
clear
[alphabet,targets]=prprob;
[R,Q]=size(alphabet);
[S2,Q]=size(targets);
S1=10;
net=newff(minmax(alphabet),[S1 S2],...
...{′logsig′ ′logsig′},′traingdx′);
net.LW{2,1}=net.LW{2,1}*0.01;
net.b{2}=net.b{2}*0.01;
net.performFcn='sse';
net.trainParam.goal=0.1;
net.trainParam.epochs=5000;
net.trainParam.mc=0.95;
P=alphabet;
T=targets;
[net,tr]=train(net,P,T);
通过这一部分的学习,可使学生对神经网络算法有更具体的认识,也实践了神经网络软件设计的手段。
2 神经网络FPGA硬件实现
2.1 硬件设计框架
利用硬件描述语言Verilog对软件设计得到的神经网络算法进行硬件化,实现相应的端口定义、内部寄存器定义、输出计算结果和训练过程。实验中,训练过程采用状态机进行表述,使学生对主要的FPGA硬件设计手段更加熟悉[7]。其中主要的训练过程Verilog代码如下:
parameter N01=5'b00000,N02=5'b00001,…
always@(posedge clk)
begin
if(!rst)
state<=N01;
else
begin n0<=1;n1<=1;n2<=0;n3<=0;n4<=1;n5<=0;n6<=0;n7<=1;n8<=1;end
case(state)
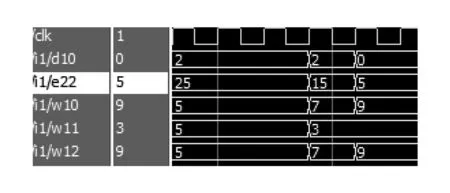
N01:if(3 …… 以3×3图像为例,误差计算公式如下: Δij(n)=ei(n)Wj(n) 由于该网络的规模较小,可预先将教师信号储存于寄存器中,直接代入误差公式计算。 网络训练中,权值更新计算如下: 其中A为设置的幅值,A偏大则不容易停留在理想值周边,甚至有可能处于权值允许范围的上下限之外,A偏小则权值更新速度较慢,所以需要结合实际情况进行修改。sgn函数标记修正量的正负,从而实现双向的修正。在硬件设计中可以通过比较器的方式方便快捷地实现该sgn函数的计算。 传递函数在BP网络中起着信息传播的重要作用。本实验选择的算法为 fi=tanh(Ii) 上式传递函数为双曲正切函数。考虑到在FPGA里实现这类反三角函数一直是算法硬件化的难点之一,对其进行分解: 通过计算sinh和cosh函数的值,进而利用除法器得到tanh函数的结果。 具体而言,实验中选择cordic算法使传递函数得到实现。cordic的实质是循环迭代[8],其核心是先固定一些基准角,再通过不断地摇摆每一个基准角逼近目标角度值。在x-y直角坐标轴中将点(x1,y1)旋转到(x2,y2,旋转角为θ,其原理示意如图3所示: 图3 cordic算法坐标旋转示意图 使用Verilog语言编写的cordic算法核心部分如下: module cordic(dat,clk,done,rst_); input[10:0] dat; input clk,rst_; output reg signed [33:0] done; …… case(state) A0: begin out_sinh<=0; out_cosh<=0; done<=0; state<=A1; end A1: begin x1[26:0]<=27'h26A3AD2; y1[26:0]<=27'h0; z1[26:0]<=dat_in; state<=A2; end A2: begin if(!z1[26]) begin x2[26:0]<=x1[26:0]+{{1{y1[26]}},y1[26:1]}; y2[26:0]<=y1[26:0]+{{x1[26]},x1[26:1]}; z2[26:0]<=z1[26:0]-27'h1193EA8; state<=A3; end else begin x2[26:0]<=x1[26:0]-{{1{y1[26]}},y1[26:1]}; y2[26:0]<=y1[26:0]-{{x1[26]},x1[26:1]}; z2[26:0]<=z1[26:0]+27'h1193EA8; state<=A3; end end …… 编写testbench,对训练和测试部分分别进行测试,并使用Modelsim进行波形仿真,使学生对硬件设计的验证以及优化手段有很好的掌握[9]。在神经网络的训练过程中,得到的权值与误差的仿真波形如图4所示: 图4 训练过程权值误差波形仿真图 图中表示误差的e22随着训练逐渐减小,权值变化量d22也随着误差减小,最终减小为0,即宣告神经网络训练完成。 用前述30幅带误差的二值图像作为测试数据集进行验证,仿真波形如图5所示: 此波形中,输出数据最大的那一行即为正确分类。训练结果表明:所有图像均分类正确,硬件实现的网络的识别效果非常好。 图5 神经网络测试波形仿真图 在功能正确的基础上,可进行硬件优化,提高电路的性能。例如删除不必要的乘法、精简电路结构;将复杂组合逻辑写入独立的时序逻辑中[10],提高电路频率。以一个具体优化为例,对于最影响电路时序的路径(dataout输出路径),其为各权值与输入乘积的和,而乘法器占用资源与处理速度均较慢。考虑到其输入均为一位,所以可在实验中采用选择器取代乘法器,从而降低资源消耗。此外,对电路做流水线处理,采用SPEED模式作为综合策略[11],可对整体进行速度优化。在FPGA型号选择为Cyclone II:EP2C35F672C6N的情况下,优化后的硬件性能达到总资源187,组合逻辑89,时钟频率208.86 MHz。 最终的板级验证,使用DEII FPGA开发平台上的七位数码管展示测试得到的分类结果。图6所示分类结果为第二类,即字母V。 图6 分类功能板级验证 以神经网络为代表的机器学习硬件设计,是人工智能的一个重要发展方向。通过机器学习FPGA硬件实验,使学生既能对神经网络算法有个基本的认识,也能对主流实现手段有深入的掌握,有助于学生理解硬件设计以及各种优化设计的方式[12]。 此基于FPGA平台的机器学习硬件实验具有很强的开放性和拓展性。在熟悉神经网络结构和算法、神经网络工具箱调用、FPGA设计及硬件优化等环节中均可为学生提供自主学习和拓展的空间。例如在算法熟悉阶段,设计了一个学生讲授自己通过查阅资料对机器学习理解的环节;在硬件优化阶段,设计了一个由学生自行探索优化手段的环节。通过此类翻转课堂教学手段的导入,培养了学生的独立思考能力和创新精神,取得了良好的实验教学效果。2.2 传递函数的FPGA实现
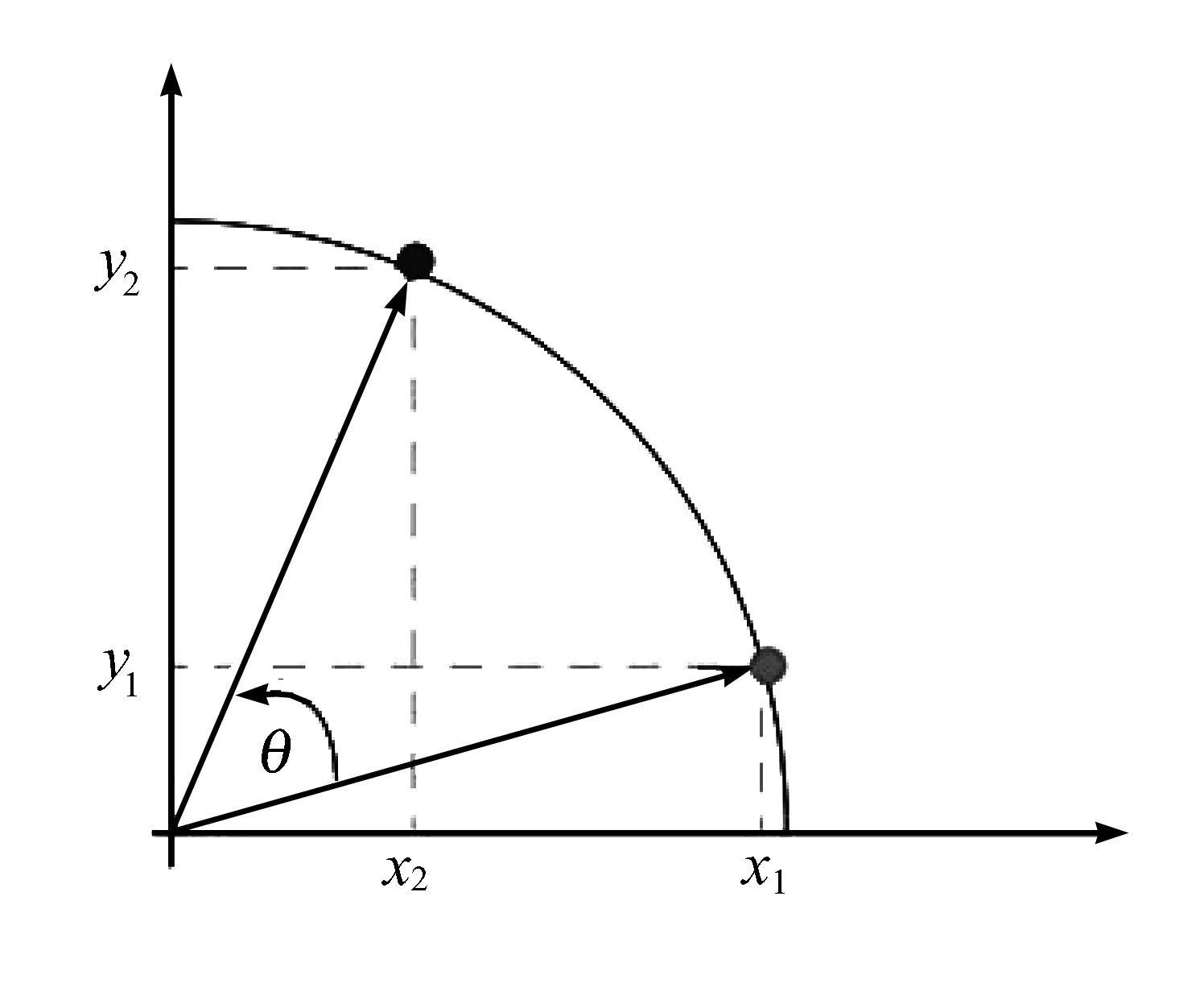
3 结果测试和硬件优化


4 结语
