基于大规模定制生产的设备布局模拟系统设计

熊佳玮, 樊树海, 张文倩

(1. 南京工业大学 工业工程系, 南京 210009； 2. 麻省理工学院信息质量项目“数据质量与信息安全”实验室, 美国马萨诸塞州 02139)

虚拟仿真教学作为传统教学的辅助方式,可以大大地提升研究和教学效率[1],也解决了一些实验可操作性不强、实验思想难以实现的问题。虚拟仿真实验教学已成为实验教学改革的重要内容和必然趋势。

随着工业自动化、集成化水平的提高和大规模定制生产模式的兴起,模拟制造成为高校相关专业实验教学的热点。为了提高车间物流效率,实验中往往会使用SLP等方法实现设备布局,但是这些方法在确认模拟车间布局后就不再会去移动实验机台[2-3]。一旦生产线设备出现变动需要增加机台则难以快速重构。为了提高实验室机台的可重构性,笔者基于大规模定制理论和GA-Layout(一种改进的遗传算法)对仿真生产实验平台进行设计与开发。

1 仿真实验平台分析

设备布局是指按照一定的设计规则,在既定数量加工单元和车间内部空间的约束下,对车间内的各加工单元、暂存地以及组成部分进行优化布置,使之配合良好，达到最低的物流运送成本。在进行车间布局时要考虑的因素主要有车间布局的柔性、敏捷性、可重构性以及鲁棒性[4]。

车间布局问题历来是一个很复杂的问题,其约束条件一般有设备摆放空间的限制、被布局设备的集合、设备之间的距离约束、产品的加工工艺顺序、大型设备不可移动的限制等。此外,车间可重构布局还需要考虑布局成本和设备位置重构成本尽可能低[5]、物流成本更低。

2 模拟系统方案设计

2.1 系统功能框架设计

模拟系统的系统由学生端和服务器端组成。学生端负责上传实验预设、参数传给服务器,服务器端运算并将返回值矩阵和坐标传到学生端Flexsim接口进行可视化输出。实际系统流程如图1所示：

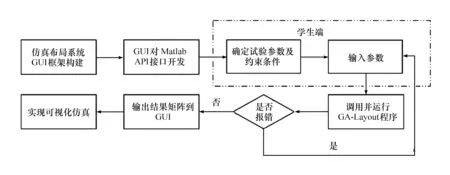
图1 系统框架

2.2 仿真布局系统参数设计

在实验车间布局空间里存在n个设备单元,在相关参数中,L为可用空间长度,H为可用空间宽度,M为设备总集,M={m1,m2,…,mn}；rij为设备i和设备j之间每单位物料在每单位距离上的搬运费用；Rij为设备间运输费用矩阵；sij为设备i和设备j之间的运输频率；Sij为设备间运输频率矩阵；hij为设备i和设备j之间最小横向距离要求；Hij为设备间最小横向距离要求矩阵；Hi0为设备i和车间边界的最小横向间距限制；(xi,yi)是设备i的坐标。

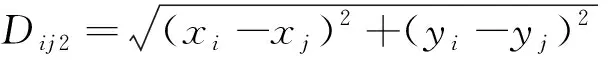
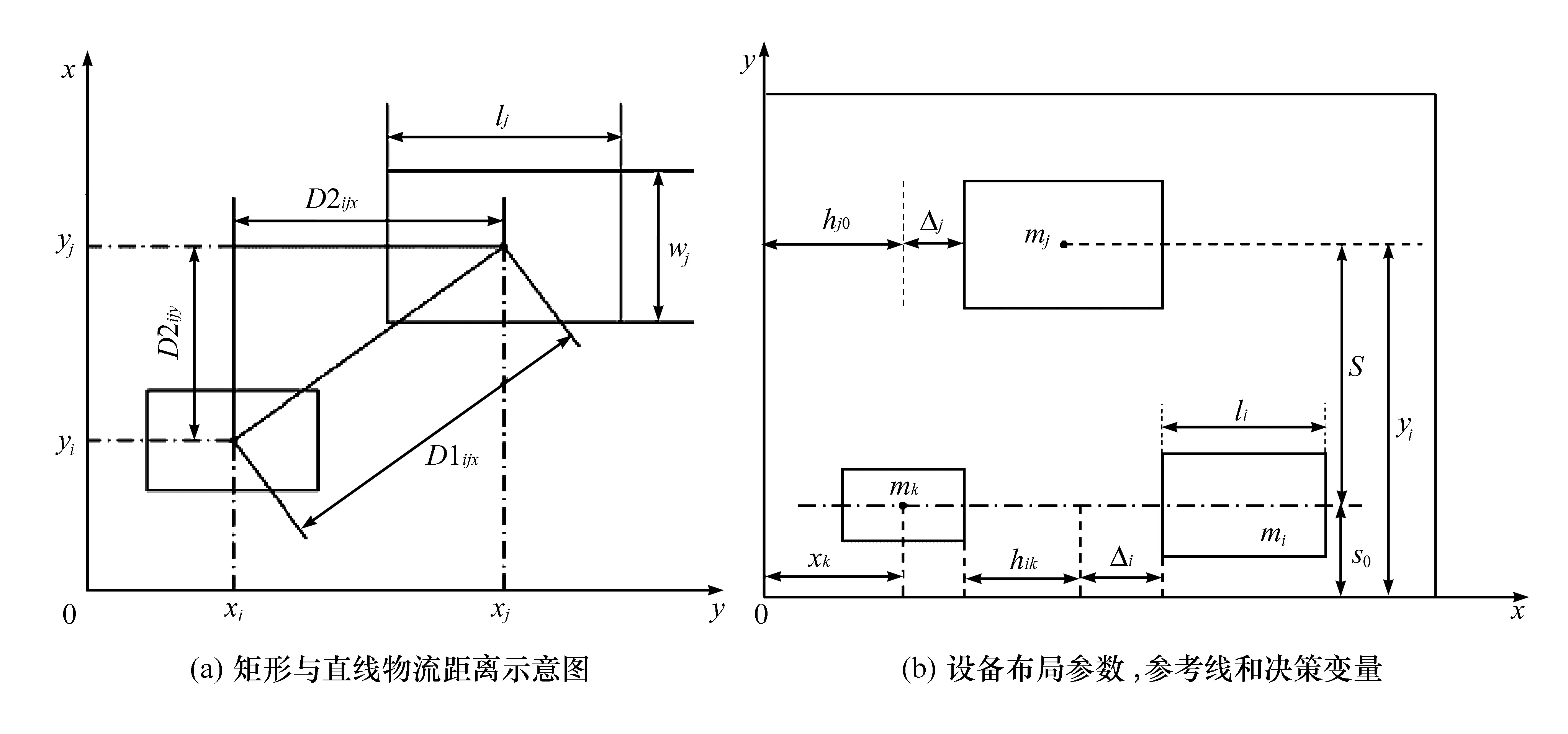
图2 实验车间布局的参数几何表达

2.3 仿真布局系统约束设计

对于需要重新布局的车间,初次摆放好的设备能否进行二次、甚至多次重组及数量变动,是可重构性的重要指标[2]。可重构度以设备间实际去心距离在满足移动需要的前提下,将物流运输成本的最小化作为判别标准。为了满足空间大小和实体不重叠的要求,需确定2个约束条件。

2.3.1 横纵坐标及边界约束

对于i,j∈{1,2,…,n},满足|xi-xj|≥(li+lj)/2+hxij,|yi-yj|≥(wi+wj)/2+hyij。为了简化编程计算,定义Δi为设备i和设备i-1或者设备和边界之间的净距离,即除去设备间最小距离要求hij之外的剩余距离,其取值范围是[0,1.7]；一般车间为了满足叉车等运输设备入场以及消防通道的建设,多行设备的行间距一般固定某一个数值,这里取s。设第一行设备与车间下边界距离为s0,建立设备i横、纵坐标公式：

(1)

yi=(k-1)s+s0

(2)

为了简便说明,假设xk和车间边界相邻,从而推出xk=hk0+Δk+lk/2。同时这也是一个递推公式,为遗传算法排序染色体的方便,在确定了第一行的第一个设备的横坐标之后,可以根据自动换行和求解规则确定其他设备的横坐标。

2.3.2 确定设备独立约束

为满足设备搬动以及设备不重合的要求,确定设备独立约束为

|xi-xj|≥[((li+lj))/2+hij]zikzjk

i,j=1,2,…,n

(3)

其中

(4)

i=1,2,…,n;k=1,2,…,m

xi≥0；yi≥0；Δi≥0；i=1,2,…,n

(5)

3 仿真环境搭建及程序设计

3.1 GUI构建及接口开发

使用Python搭建GUI框架并调用GA-Layout.m作为算法核心,返回值录入GUI系统显示,其调用指令如下：

cd ″matlabrootexternenginespython″

python setup.py install

import matlab.engine

eng = matlab.engine.start_matlab()

pyga=GA-Layout(chrx,MOC,PkG,LayoutG)

print(pyga)

true

1.融入领导机制。坚持和完善“双向进入、交叉任职”的领导机制，全面推行党组织书记、董事长、法人代表“一肩挑”的领导设置模式，将党委会研究讨论作为董事会、经理层决策重大问题的前置程序。同时将党建工作总体要求纳入公司章程，明确了党组织在公司治理中的法定地位。同时按照国有企业领导人员“20字标准”，加强干部队伍建设，培养和选拔后备干部，引进高层次技术、管理人才。

3.2 GA-Layout算法编写

根据遗传算法的语言特点,结合本问题进行具体程序编写。编码结构主要由以下几个部分组成[6-9]：

(1) 编码：编码使用设备号与设备净间距混合进行实数编码：

[{m1,m2,…,mn},{Δ1,Δ2,…,Δn}]

mi代表设备序号；Δi代表净间距。同时,算法采用自动换行原理；

(2) 创建初始种群,采用随机产生；

(3) 惩罚函数：由于在x轴方向上采取了自动换行的策略,横向布局不会出现超出最大长度限制的情况,所以只需判别方案中设备在y轴方向上是否超过车间最大宽度限制,建立惩罚函数Pk：

(6)

其中H为车间最大宽度；Pk为纵坐标超出惩罚项；T为一个为正且数值较大的惩罚值,根据情况不同一般取500～10 000；

(4) 适应度函数：依据上文所提出的中心直线距离确定适应度函数

Fitnessfunc=1/(C1min+Pk)=

(5) 选择：采用随机竞争轮盘赌法(stochastic tournament-roulette wheel selection),是一种放回式随机采样方法[10],在标准轮盘赌法中加入随机竞争操作,即每次使用轮盘赌操作的时候选取一对个体,让这两个个体单独竞争,留下适应度高的个体,如此循环,直到选满；

(6) 交叉：由于采用了两组数据编码,所以使用部分映射交叉(part-mapping crossover)对设备序号染色体进行交叉,算数交叉用来处理净间距染色体[11]。

部分映射交叉是随机选取2个交叉点,对两点内需要交叉的部分逐个进行交叉,同时对交叉后形成的重复符号进行修正,以得到新的个体,交叉规则如图3所示。

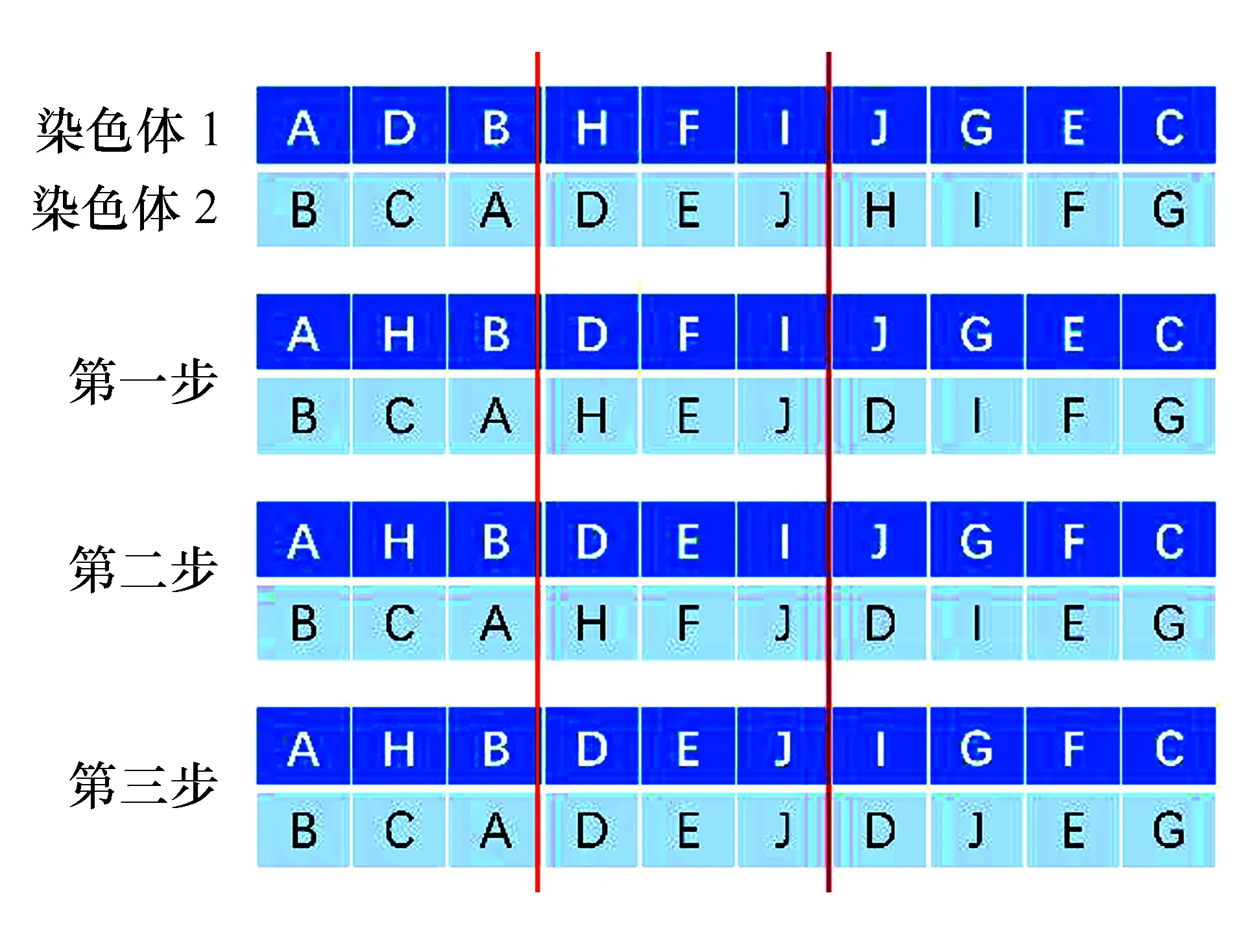
图3 PMC交叉示意图

算数交叉是由2个个体的线性组合而产生2个新的个体。为了能够进行线性运算,一般编码方式都为浮点数编码[12]。

(7)

其中,a为一个固定参数。

(7) 变异：由于设备序号染色体为整数编码,所以只对设备净间距进行变异。净间距染色体为

[…,{Δ1,Δ2,…,Δi,…,Δn}]

4 仿真实验结果分析与三维输出

本文采用Matlab的M#语言实现基于遗传算法的GA-Layout布局优化算法(以下简称GALA)。实验所用的计算机操作系统为Windows 10。在以往实验的基础上,设置该算法初始参数为：种群数量nchr=50,遗传代数G=400,交叉概率pc=0.65,变异概率pm=0.1,大数惩罚值T=1 000,变异过程中的区间段r=12。

仿真生产实验室可以近似的看作一个长11 m、宽9 m的矩形空间。现要加入3台设备,共计布置12台设备,设备尺寸DeviceSize,设备之间单位距离运输费用Rij,运输频率Sij,设备间最小横向距离要求Hij,边界约束Hi0如表1所示：

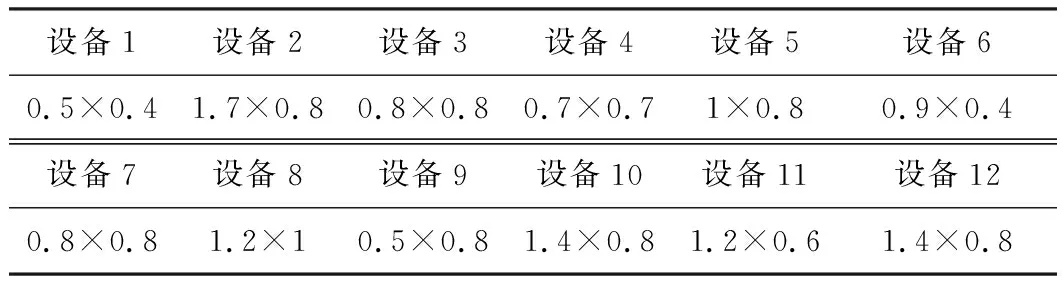
表1 设备尺寸 (m)

为了能够缩短寻优过程,使用传统SLP方法获得一组初始可行解[2 8 5 4 11 1 7 3 12 9 10 6],作为GA-Layout的初始解。对该算法进行15次运算,取最优一次结果得到Layout矩阵为([1x3 double],[1x4double],[1x3 double],[1x2 double]),说明布局方式为第一行3个,第二行4个,第三行3个,第四行2个；产生最优解的代数为127代,最优解为2840。进化与收敛曲线如图4所示。设备中心点坐标为：(9.34,3.7)、(7.21,3.7)、(2.0,3.7)、(1.75,5.7)、(1.28,1.7) 、(3.99,1.7)、(3.93,3.7)、(3.50,7.7)、(4.97,5.7)、(1.08,7.7)、(6.17,1.7)、(7.56,5.7)。

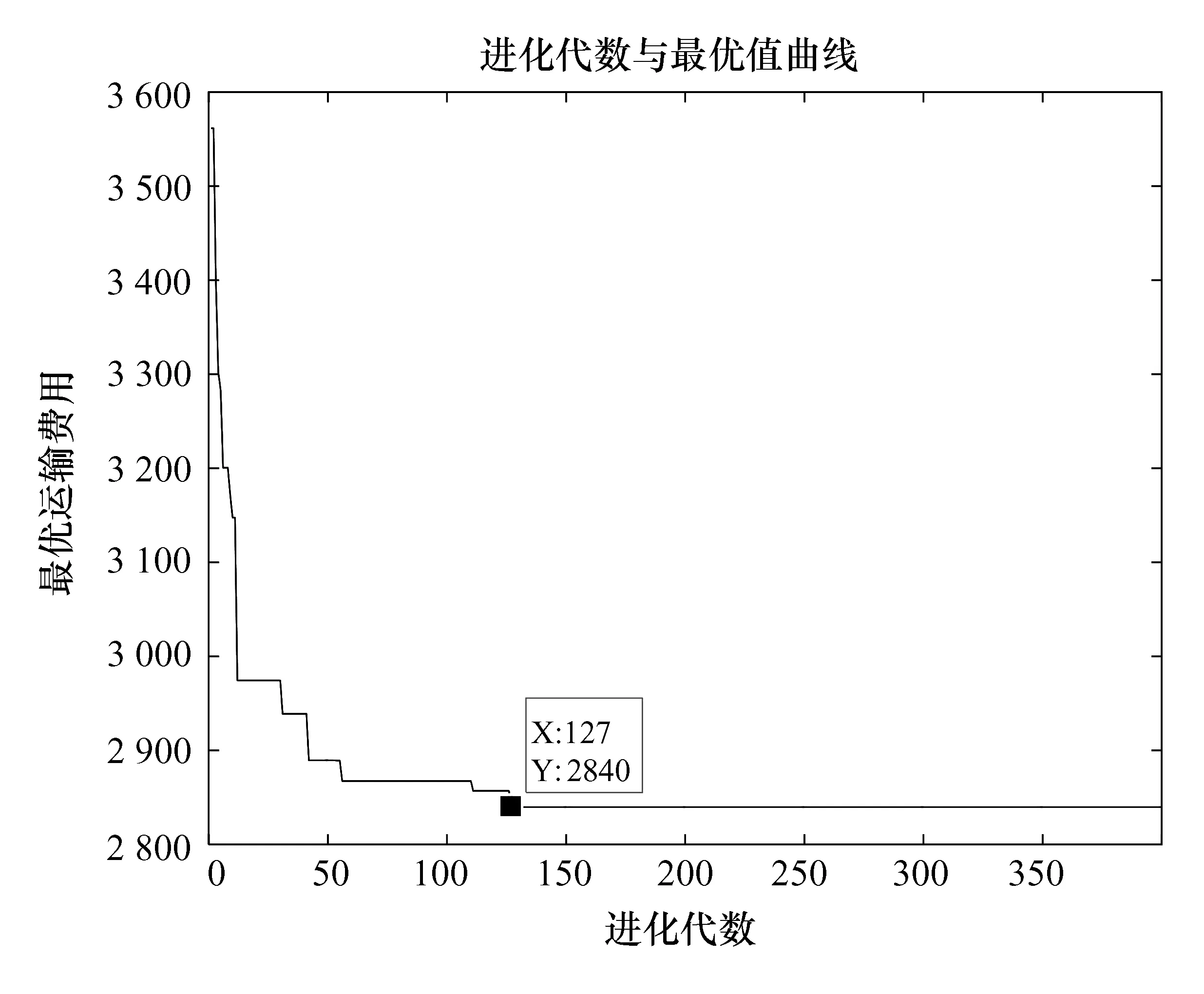
图4 直线距离收敛

结果矩阵返回GUI，并通过Python的API接口导入Flexsim进行可视化仿真输出,仿真可视化结果如图5所示。

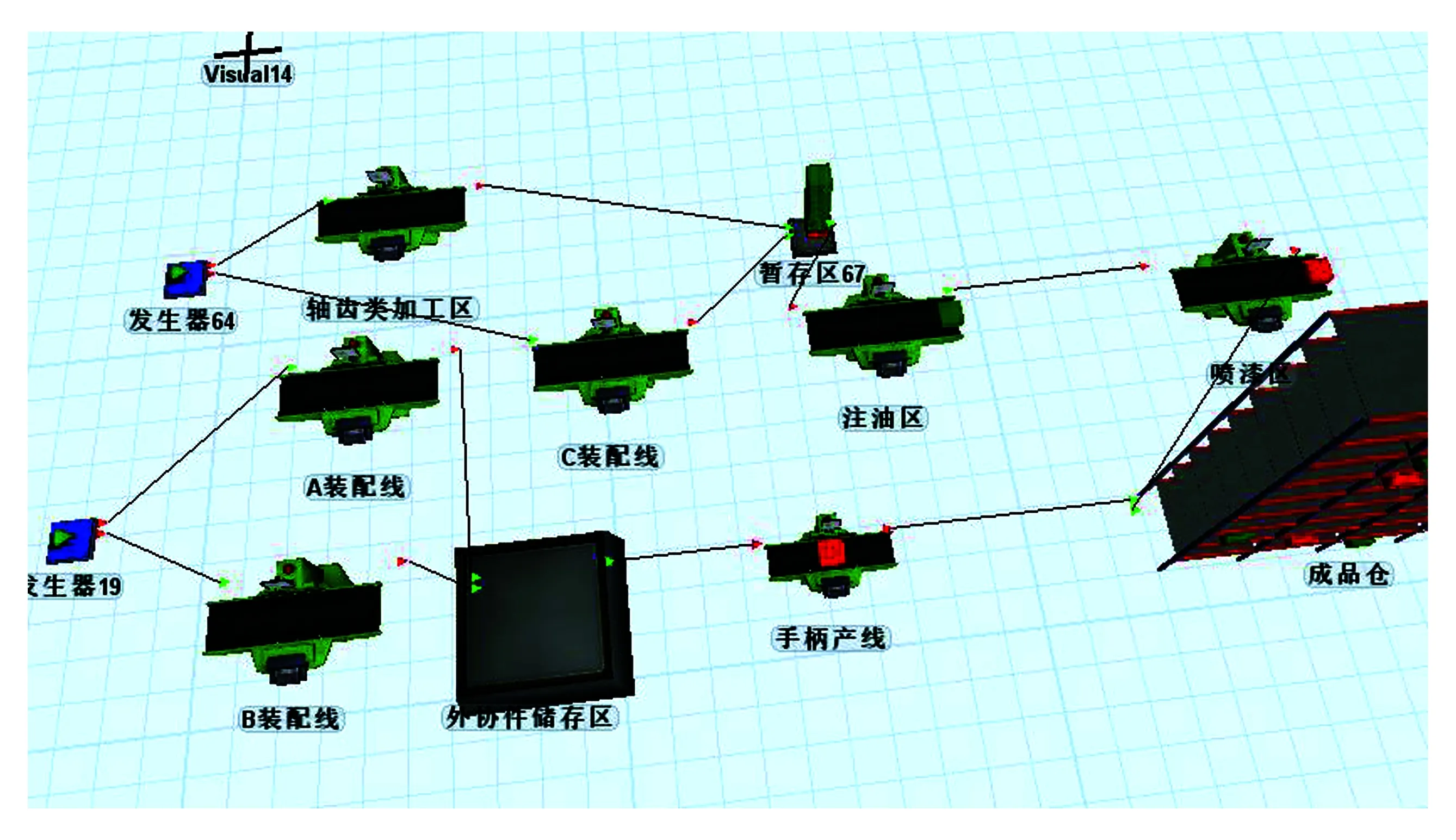
图5 Flexsim可视化仿真图

5 结语

基于Matlab和Python的定制生产可变布局仿真系统实验效果良好。通过改进的遗传算法可以快速地得出最优解,避免了以往SLP效率低下的问题。GA-Layout程序的良好开放性和模块化的设计思路可以让学生自行开发端口、集成更多的专业软件,并且可以根据具体实验需求增减、改变约束条件和初值等参数,以适应不用阶段学生的实验需求。算法中的实数编码可使导出数据简洁明了,避免了和其他软件I/O接口的二次转化。Flexsim的应用使得实验数据可以迅速仿真并导出为三维视图,为进一步实验和IGRIP人因系统仿真提供良好的基础。计算机仿真的应用使得实验难点变得具象化、可视化和动态化,能够有效地避免实验课程程式化、机械化,有效促进学生的实验积极性和创新意识。